Уравнение Бернулли и следствия из него

Выделим в стационарно текущей идеальной жидкости трубку то­ка, ограниченную сечениями S₁ и S₂, по которой слева направо течет жидкость. Пусть в месте сечения S₁ скорость течения 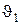, давление р₁ и высота, на которой это сечение расположено, h₁. Аналогично, в месте сечения S₂ скорость течения 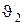, давление р₂ и высота сечения h₂. За малый промежуток времени Dt жидкость перемещается от се­чений S₁ и S₂ к сечениям S¢₁ и S¢₂.

Согласно закону сохранения энергии, изменение полной энергии Е₂-E₁ идеально несжимаемой жидкости должно быть равно рабо­те А внешних сил по перемещению массы m жидкости:

E₂ - E₁ = A, (6.2)

где Е₁ и Е₂ - полная энергия жидкости массой m в местах сечений S₁ и S₂ соответственно.

С другой стороны, А – это работа, совершаемая при перемещении всей жидкости, заключенной между сечениями S₁ и S₂, за рассматри­ваемый малый промежуток времени Dt. Для перенесения массы m от S₁ до S'₁ жидкость должна переместиться на расстояние 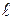₁= 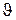₁Dt и от S₂ до S₂' - на расстояние 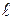₂= 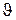₂Dt. Отметим, что 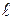₁и 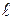₂ настолько малы, что всем точкам объемов, закрашенных на рис. 40, приписывают постоянные значения скорости 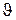, давления р и высоты h. Следовательно,

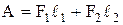, (6.3)

где F₁=p₁S₁, F₂= -p₂S₂ (отрицательна, т.к. направлена в сторону, противоположную течению жидкости, рис. 40).

Полные энергии Е₁ и Е₂ будут складываться из кинетической и потенциальной энергий массы m жидкости:

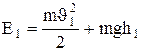(6.4)

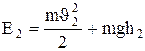. (6.5)

Подставляя (6.4) и (6.5) в (6.2) и приравнивая (6.2) и (6.3), получим

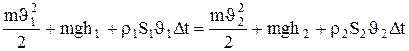. (6.6)

Согласно уравнению неразрывности для несжимаемой жидкости (6.1),

объем, занимаемый жидкостью, остается постоянным, т.е.

.

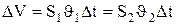Разделив выражение (6.6) на DV, получим

где r - плотность жидкости. Но т.к. сечения выбирались произво­льно, можно записать

. (6.7)

Выражение (6.7) выведено швейцарским физиком Д. Бернулли и называется уравнением Бернулли. Это выражение закона сохранения энергии применительно к установившемуся течению иде­альной жидкости. Оно хорошо выполняется и для реальных жидкос­тей, внутреннее трение которых не очень велико.

Величина р в формуле (6.7) называется статическим дав­лением, величина - динамическим давлением, величина pgh представляет собой гидростатическое давление.

Для горизонтальной трубки тока (h₁=h₂) выражение (6.7) принимает вид

,

где 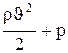– полное давление.

Из уравнения Бернулли (6.7) для горизонтальной трубки тока и уравнения неразрывности (6.1) следует, что при течении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жид­кости больше в местах сужения, а статическое давление больше в более широких местах, т.е. там, где скорость меньше.

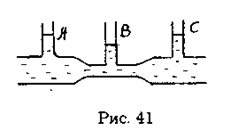
Это можно продемонстриро­вать, установив вдоль трубы ряд манометров (рис. 41) В соответствии с уравнением Бернулли опыт показывает, что в ма­нометрической трубке В, прикрепленной к узкой части трубы, уровень

жидкости ниже, чем в манометрических трубках А и С, прикрепленных к широкой части трубы.

Так как динамическое давление связано со скоростью движения жид­кости (газа), то уравнение Бернулли позволяет измерять скорость по­тока жидкости.

Уравнение Бернулли используется для нахождения скорости исте­чения жидкости через отверстие в стенке или дне сосуда.

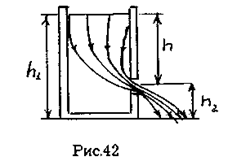
Рассмотрим цилиндрический сосуд с жидкостью, в боковой стенке кото­рого на некоторой глубине ниже уровня жидкости имеется маленькое отверстие (рис.42).

Рассмотрим два сечения (на уровне h₁ свободной поверхности жи­дкости в сосуде и на уровне h₂ выхода ее из отверстия). Напишем для них уравнение Бернулли:

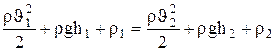
Так как давления p₁ и р₂ в жидкости на уровнях первого и второго сечений равны атмосферному, т.е. р₁=р₂, то уравнение будет иметь вид

.

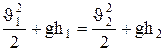Из уравнения неразрывности (6.1) следует, что 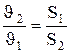, где S₁ и S₂ – площади поперечных сечений сосуда и отверстия. Если S₁>>S₂, то членом 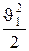мож-

но пренебречь и

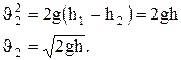
Это выражение получило название формулы Торричелли.

Дата добавления: 2014-11-16