Исследование устройств кодирования и декодирования помехоустойчивых кодов. Коды Хемминга

Лабораторная работа № 7

Контрольные вопросы

1. В чем сущность поэлементной и групповой синхронизации?
2. Объясните причины, вызывающие необходимость использования в системах передачи дискретных сообщений устройств поэлементной синхронизации.
3. Поясните принцип работы, достоинства и недостатки резонансного устройства синхронизации.
4. Поясните принцип работы, достоинства и недостатки замкнутых устройств синхронизации по сравнению с разомкнутыми.
5. Каковы преимущества устройства синхронизации без непосредственного воздействия на частоту задающего генератора по сравнению с устройством с непосредственным воздействием?
6. Какими параметрами характеризуется устройство синхронизации?
7. Объясните методику расчета параметров устройства синхронизации без непосредственного воздействия на частоту генератора.
8. Как объяснить влияние погрешности синхронизации на верность приема единичного элемента?
9. Как рассчитать влияние погрешности синхронизации на верность приема единичного элемента?
10. Для чего используется маркер при установлении цикловой синхронизации?
11. Функции УЦС в режиме поиска маркера.
12. Функции выполняет УЦС в режиме удержания цикловой синхронизации.
13. От чего зависит время восстановления цикловой синхронизации?
14. Как влияет структура маркера на процесс цикловой синхронизации?

Цель работы: изучение принципов помехоустойчивого кодирования, ознакомление с основными характеристиками, с методами кодирования и декодирования.

1. Краткие теоретические сведения

1.1 Принципы помехоустойчивого кодирования.

В реальных условиях приём двоичных символов всегда происходит с ошибками, когда вместо символа "1" принимается символ "0" и наоборот. Ошибки могут возникать из-за помех, действующих в канале связи (особенно помех импульсного характера), изменения за время передачи характеристик канала (например, замирания), снижения уровня передачи, нестабильности амплитудно- и фазочастотных характеристик канала и т.п.

Общепринятым критерием оценки качества передачи в дискретных каналах является нормированная на знак или символ допустимая вероятность ошибки для данного вида сообщений. Так, допустимая вероятность ошибки при телеграфной связи может составлять 10^-3 (на знак), а при передаче данных – не более 10^-6 (на символ). Для обеспечения таких значений вероятностей одного улучшения только качественных показателей канала связи может оказаться недостаточным. Поэтому основной мерой является применение специальных методов повышения качества приёма передаваемой информации. Эти методы можно разбить на две группы.

К первой группе относятся методы увеличения помехоустойчивости приёма единичных элементов (символов) дискретной информации, связанные с выбором уровня сигнала, отношения сигнал-помеха (энергетические характеристики), ширины полосы канала, методов приёма и т.д.

Ко второй группе относятся методы обнаружения и исправления ошибок, основанные на искусственном введении избыточности в передаваемое сообщение. Увеличить избыточность передаваемого сигнала можно различными способами. Так как объём сигнала

V = P ⋅ ∆F ⋅ T, (1)

где P - мощность сигнала, Вт; ∆F - ширина спектра сигнала, Гц;

T - время передачи сигнала, сек, то его увеличение возможно за счёт увеличения P, ∆F и T.

Практические возможности увеличения избыточности за счёт мощности и ширины спектра сигнала в системах передачи дискретной информации по стандартным каналам резко ограничены. Поэтому для повышения качества приёма, как правило, идут по пути увеличения времени передачи и используют следующие основные способы:

1) многократная передача кодовых комбинаций (метод повторения);

2) одновременная передача кодовой комбинации по нескольким параллельно работающим каналам;

3) помехоустойчивое (корректирующее) кодирование, т.е. использование кодов, исправляющих ошибки.

Иногда применяют комбинации этих способов.

Многократное повторение (ℓ раз) кодовой комбинации является самым простым способом повышения достоверности приёма и легко реализуется, особенно в низкоскоростных системах передачи для каналов с быстро меняющимися параметрами. Способу многократного повторения аналогичен способ передачи одной и той же информации по нескольким параллельным каналам связи. В этом случае необходимо иметь не менее трёх каналов связи (например, с частотным разнесением), несущие частоты которых нужно выбирать таким образом, чтобы ошибки в каналах были независимы. Достоинством таких систем являются надёжность и малое время задержки в получении информации. Основным недостатком многоканальных систем так же, как и систем с повторением, является нерациональное использование избыточности.

Наиболее целесообразно избыточность используется при применении помехоустойчивых (корректирующих) кодов.

При помехоустойчивом кодировании чаще всего считают, что избыточность источника сообщений на входе кодера равна χ = 0. Это обусловлено тем, что очень многие дискретные источники (например, цифровая информация на выходе ЭВМ) обладают малой избыточностью. Если избыточность первичных источников сообщений существенна, то в этих случаях по возможности стремятся ее уменьшить путём эффективного кодирования, применяя, например, коды Шеннона-Фано или Хафмена. Затем методами помехоустойчивого кодирования можно внести такую избыточность в сигнал, которая позволит достаточно простыми средствами улучшить качество приёма. Таким образом, эффективное кодирование вполне может сочетаться с помехоустойчивым.

В обычном равномерном непомехоустойчивом коде число разрядов n в кодовых комбинациях определяется числом сообщений и основанием кода.

Коды, у которых все кодовые комбинации разрешены к передаче, называются простыми или равнодоступными и являются полностью безизбыточными. Безизбыточные первичные коды обладают большой "чувствительностью" к помехам.

Внесение избыточности при использовании помехоустойчивых кодов обязательно связано с увеличением n - числа разрядов (длины) кодовой комбинации. Таким образом, всё множество N = 2ⁿ комбинаций можно разбить на два подмножества: подмножество разрешённых комбинаций, т.е. обладающих определёнными признаками, и подмножество запрещённых комбинаций, этими признаками не обладающих.

Помехоустойчивый код отличается от обычного тем, что в канал передаются не все кодовые комбинации N, которые можно сформировать из имеющегося числа разрядов n, а только их часть N_К, которая составляет подмножество разрешённых комбинаций.Если при приёме выясняется, что кодовая комбинация принадлежит к запрещённым, то это свидетельствует о наличии ошибок в комбинации, т.е. таким образом решается задача обнаружения ошибок. При этом принятая комбинация не декодируется (не принимается решение о переданном сообщении). В связи с этим помехоустойчивые коды называют корректирующими кодами. Корректирующие свойства избыточных кодов зависят от правила их построения, определяющего структуру кода, и параметров кода (длительности символов, числа разрядов, избыточности и т.п.).

Первые работы по корректирующим кодам принадлежат Хеммингу, который ввёл понятие минимального кодового расстояния d_min и предложил код, позволяющий однозначно указать ту позицию в кодовой комбинации, где произошла ошибка. К "k" информационным элементам в коде Хемминга добавляется "r" проверочных элементов для автоматического определения местоположения ошибочного символа. Коды Хемминга будут рассмотрены подробнее далее.

1.2. Основные характеристики корректирующих кодов.

В настоящее время наибольшее внимание с точки зрения технических приложений уделяется двоичным блочным корректирующим кодам. При использовании блочных кодов цифровая информация передаётся в виде отдельных кодовых комбинаций (блоков) равной длины. Кодирование и декодирование каждого блока осуществляется независимо друг от друга.

Почти все блочные коды относятся к разделимым кодам, кодовые комбинации которых состоят из двух частей: информационной и проверочной. При общем числе n символов в блоке число информационных символов равно k, а число проверочных символов

r = n – k. (2)

К основным характеристикам корректирующих кодов относятся:

− число разрешённых и запрещённых кодовых комбинаций;

− избыточность кода;

− минимальное кодовое расстояние;

− число обнаруживаемых или исправляемых ошибок;

− корректирующие возможности кодов.

Число разрешённых и запрещённых кодовых комбинаций.

Для блочных двоичных кодов, с числом символов в блоках равным n, общее число возможных кодовых комбинаций определяется значением

N₀ = 2ⁿ. (3)

Число разрешённых кодовых комбинаций при наличии k информационных

разрядов в первичном коде равно

N_k = 2^k. (4)

Очевидно, что число запрещённых комбинаций равно:

N_З = N₀ - N_k = 2ⁿ –2^k, (5)

а с учётом (3.2) отношение будет:

N₀ / N_k = 2ⁿ / 2^k = 2^{n- k} = 2^r, (6)

где r -число избыточных (проверочных) разрядов в блочном коде.

Избыточность корректирующего кода.

Избыточностью корректирующего кода называют величину

,

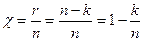(7)

откуда следует

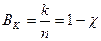(8)

Эта величина показывает, какую часть общего числа символов кодовой комбинации составляют информационные символы. В теории кодирования величину B_k называют относительной скоростью кода. Если производительность источника информации равна H символов в секунду, то скорость передачи после кодирования этой информации окажется равной

,

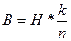(9)

поскольку в закодированной последовательности из каждых n символов только к символов являются информационными.

Если число ошибок, которые нужно обнаружить или исправить, значительно, то необходимо иметь код с большим числом проверочных символов. Чтобы при этом скорость передачи оставалась достаточно высокой, необходимо в каждом кодовом блоке одновременно увеличивать как общее число символов, так и число информационных символов. При этом длительность кодовых блоков будет существенно возрастать, что приведёт к задержке информации при передаче и приёме. Чем сложнее кодирование, тем длительнее временная задержка информации.

Минимальное кодовое расстояние - d_min.

Для того, чтобы можно было обнаружить и исправлять ошибки, разрешённая комбинация должна как можно больше отличаться от запрещённой. Если ошибки в канале связи действуют независимо, то вероятность преобразования одной кодовой комбинации в другую будет тем меньше, чем большим числом символов они различаются.

Если интерпретировать кодовые комбинации как точки в пространстве, то отличие выражается в близости этих точек, т.е. в расстоянии между ними.

Количество разрядов (символов), которыми отличаются две кодовые комбинации, можно принять за кодовое расстояние между ними. Для определения этого расстояния нужно сложить две кодовые комбинации по модулю 2 и подсчитать число единиц в полученной сумме. Например, две кодовые комбинации x_i = 01011 и x_j = 10010 имеют расстояние d(x_i,x_j), равное 3, так как

x_i = 01011 → W = 3

Å

x_j = 10010 → W = 2

x_i Å x_j = 11001 → d(x_i,x_j) = 3. (10)

(Здесь под операцией "Å" понимается сложение по mod2).

Заметим, что кодовое расстояние d(x_i, x₀) между комбинацией x_i и нулевой x₀ = 00..0 называют весом W комбинации x_i, т.е. вес xi равен числу "1" в ней.

Расстояние между различными комбинациями некоторого конкретного кода могут существенно отличаться. Так, в частности, в безизбыточном первичном натуральном коде (n = k) это расстояние для различных комбинаций может изменяться от единицы до величины n, равной значности кода. Особую важность для характеристики корректирующих свойств кода имеет минимальное кодовое расстояние d_min, определяемое при попарном сравнении всех кодовых комбинаций, которое называют расстоянием Хемминга.

В безизбыточном коде все комбинации являются разрешёнными, и, следовательно, его минимальное кодовое расстояние равно единице - d_min = 1. Поэтому достаточно исказиться одному символу, чтобы вместо переданной комбинации была принята другая разрешённая комбинация. Чтобы код обладал корректирующими свойствами, необходимо ввести в него некоторую избыточность, которая обеспечивала бы минимальное расстояние между любыми двумя разрешёнными комбинациями не менее двух - d_min ≥ 2.

Минимальное кодовое расстояние является важнейшей характеристикой помехоустойчивых кодов, указывающей на гарантируемое число обнаруживаемых или исправляемых заданным кодом ошибок.

Число обнаруживаемых или исправляемых ошибок.

При применении двоичных кодов учитывают только дискретные искажения, при которых единица переходит в нуль (1 → 0) или нуль переходит в единицу (0 → 1). Переход 1 → 0 или 0 → 1 только в одном элементе кодовой комбинации называют единичной ошибкой (единичным искажением). В общем случае под кратностью ошибки подразумевают число позиций кодовой комбинации, на которых под действием помехи одни символы оказались заменёнными на другие. Возможны двукратные (g = 2) и многократные (g > 2) искажения элементов в кодовой комбинации в пределах 0 ≤ g ≤ n.

Минимальное кодовое расстояние является основным параметром, характеризующим корректирующие способности данного кода. Если код используется только для обнаружения ошибок кратностью g₀, то необходимо и достаточно, чтобы минимальное кодовое расстояние было равно

d_min ≥ g₀ + 1. (11)

В этом случае никакая комбинация из g₀ ошибок не может перевести одну разрешённую кодовую комбинацию в другую разрешённую. Таким образом, условие обнаружения всех ошибок кратностью g₀ можно записать в виде:

g₀ ≤ d _min – 1. (12)

Чтобы можно было исправить все ошибки кратностью g и и менее, необходимо иметь минимальное расстояние, удовлетворяющее условию:

d_min ≥ 2 ⋅ g_и + 1. (13)

В этом случае любая кодовая комбинация с числом ошибок g_и отличается от каждой разрешённой комбинации не менее чем в g_и + 1 позициях. Если условие (3.13) не выполнено, возможен случай, когда ошибки кратности g исказят переданную комбинацию так, что она станет ближе к одной из разрешённых комбинаций, чем к переданной или даже перейдёт в другую разрешённую комбинацию. В соответствии с этим, условие исправления всех ошибок кратностью не более g_и можно записать в виде:

g_и ≤ (d_min – 1) / 2. (14)

Из (11) и (13) следует, что если код исправляет все ошибки кратностью g_и, то число ошибок, которые он может обнаружить, равно g₀ = 2 ⋅ g_и

Следует отметить, что соотношения (11) и (13) устанавливают лишь гарантированное минимальное число обнаруживаемых или исправляемых ошибок при заданном d_min и не ограничивают возможность обнаружения ошибок большей кратности. Например, простейший код с проверкой на чётность с d_min = 2 позволяет обнаруживать не только одиночные ошибки, но и любое нечётное число ошибок в пределах g₀ < n.

Корректирующие возможности кодов.

Вопрос о минимально необходимой избыточности, при которой код обладает нужными корректирующими свойствами, является одним из важнейших в теории кодирования. Этот вопрос до сих пор не получил полного решения. В настоящее время получен лишь ряд верхних и нижних оценок (границ), которые устанавливают связь между максимально возможным минимальным расстоянием корректирующего кода и его избыточностью [ 4].

Так, граница Плоткина даёт верхнюю границу кодового расстояния d_min при заданном числе разрядов n в кодовой комбинации и числе информационных разрядов k, и для двоичных кодов:

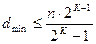(15)

или

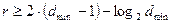(16)

при .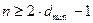

Верхняя граница Хемминга устанавливает максимально возможное число разрешённых кодовых комбинаций (2^k) любого помехоустойчивого кода при заданных значениях n и d_min:

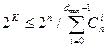(17)

где 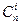- число сочетаний из n элементов по i элементам.

Отсюда можно получить выражение для оценки числа проверочных символов:

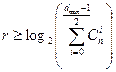(18)

Для значений (d_min / n) ≤ 0.3 разница между границей Хемминга и границей Плоткина сравнительно невелика.

Граница Варшамова-Гильберта для больших значений n определяет нижнюю границу для числа проверочных разрядов, необходимого для обеспечения заданного кодового расстояния:

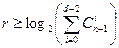(19)

Отметим, что для некоторых частных случаев Хемминг получил простые соотношения, позволяющие определить необходимое число проверочных символов [5, 6 ]:

r ≥ log₂ (n + 1) для d_min = 3,

r ≥ log₂ (2⋅n) для d_min = 4.

Блочные коды с d_min = 3 и 4 в литературе обычно называют кодами Хемминга.

Все приведённые выше оценки дают представление о верхней границе числа d_min при фиксированных значениях n и k или оценку снизу числа проверочных символов r при заданных k и d_min.

Существующие методы построения избыточных кодов решают в основном задачу нахождения такого алгоритма кодирования и декодирования, который позволял бы наиболее просто построить и реализовать код с заданным значением d_min. Поэтому различные корректирующие коды при одинаковых d_min сравниваются по сложности кодирующего и декодирующего устройств. Этот критерий является в ряде случаев определяющим при выборе того или иного кода.

Дата добавления: 2014-11-08