Моделирование кодов Хемминга в среде Матлаб

Библиотека Communications Blockset среды Матлаб поддерживает общие линейные блочные коды. Она также включает блоки, которые обрабатывают цикличные коды, коды BCH, Хэмминга и Рида-Соломона (которые являются специальными видами линейных блочных кодов). Блоки библиотеки могут закодировать или декодировать сообщение, используя один из упомянутых выше методов.

Блоки этой библиотеки разработаны для помехоустойчивого кодирования с использованием алфавитов, имеющих 2 или 2^m символов.

Функции в Communications Toolbox могут поддерживать блоки моделирования путем

1. Определения характеристик методов, таких как корректирующая способность или допустимая длина сообщения

2. Выполнения вычислений низшего уровня, связанных с методами, таких как

· Вычисление таблицы правильности (истинности?)

· Вычисление порождающей матрицы или матрицы контроля четности

· Конвертация между порождающей матрицей и матрицей контроля четности

· Вычисление порождающего полинома

Каждый блок K символов сообщения закодирован в кодовое слово, которое состоит из N символов сообщения. K называют длиной сообщения, N называют длиной кодового слова, и код называют (N, K) - кодом.

Каждое сообщение или кодовое слово является упорядоченной группой символов. Каждый блок в подбиблиотеке Block Coding обрабатывает одно слово в каждом временном шаге.

Кодирующие блоки Рида-Соломона также позволяют вам выбирать между бинарной и целочисленной информацией.

Вы можете структурировать сообщения и кодовые слова, как бинарный вектор сигналов, где каждый вектор представляет слово сообщения или кодовое слово. В установленный срок, кодирующее устройство получает все слово сообщения, кодирует его, и производит кодовое слово. Сигналы сообщения и кода разделяет то же самое типовое время.

Рисунок ниже иллюстрирует эту ситуацию. В этом примере, кодер получает четырехбитное сообщение и производит пятибитное ключевое слово в момент времени 0. Процесс повторяется с новым сообщением в момент времени 1.

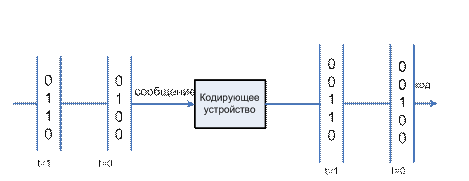
Для всех кодирующих методов, кроме кодов Рида-Соломона, используется двоичный вход, вектор сообщения должен иметь длину K и соответствующий кодовый вектор имеет длину N.

Если вход блока блочного кодирования - вектор, основанный на кадре, то он должен быть вектором – столбцом вместо вектора - строки.

Чтобы перевести основанные на отсчете сообщение в двоичный формат, вы можете конфигурировать блок Bernoulli Binary Generator так, что его параметр Probability of a zero будет вектором, длина которого есть длина сигнала, который вы хотите создать. Для того, чтобы перевести основанное на кадре сообщение в двоичный формат, вы можете конфигурировать тот же самый блок с скалярным параметром Probability of и его параметром Samples per frame, равным длине сигнала, который вы хотите создать.

Если Вы предпочитаете структурировать сообщения и кодовые слова как скалярные сигналы, где несколько отсчетов совместно формируют слово сообщения или кодовое слово, вы можете использовать блоки Buffer и Unbuffer из библиотеки Signal Processing Blockset. Знайте, что буферизование вовлекает обработка мультиуровня и время ожидания.

Если Ваша модель вычисляет скорость роста ошибок, то на начальную задержку в кодово - буферизующей комбинации влияет параметр Receive delay блока Error Rate Calculation. Если Вы не уверены в периодах дискретизации сигналов модели, выберите Sample time colors из подменю Port/signal displays меню Format модели, или присоедините блоки Probe (из библиотеки Simulink Signal Attributes) к соединителю линии могли бы помочь.

В этом разделе представим код Хэмминга с использованием бинарного формата.

Пример: Код Хэмминга в бинарном формате.

Этот пример показывает очень просто, как использовать кодер и декодер. Он иллюстрирует соответствующие размеры длины вектора кода и информационного сигнала для кодирующих блоков. Поскольку блок Error Rate Calculation принимает только скаляры или кадры векторов – столбцов как переданного и полученного сигналов, этот пример использует кадры.

(Это, таким образом, не позволяет изменить атрибуты сигнала, используя блок, такой как Convert 1-D to 2-D)

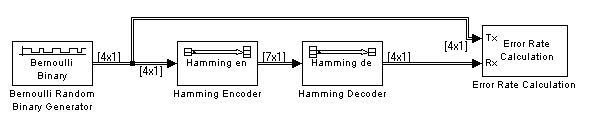
Чтобы построить модель, соберите ее и конфигурируйте блоки.

1. Блок Bernoulli Binary Generator из библиотеки Comm Sources

· Установите параметр Probability of a zero, равным 0.5.

· Установите параметр Initial seed, равным любому положительному целому числу, предпочтительно выходу функции randseed.

· Проверьте флажок Frame-based outputs.

· Установите параметр Samples per frame, равным 4.

2. Блок Hamming Encoder с значениями параметров ошибок.

3. Блок Hamming Decoder с значениями параметров ошибок.

4. Блок Error Rate Calculation из библиотеки Comm Sinks с значениями параметров ошибок.

Соедините блоки, как показано на рисунке. Используйте свойства Signal dimensions из подменю Port/signal displays меню модели Format. После обновления диаграммы в случае необходимости (Update diagram из меню Edit), линии соединителя показывают существенные признаки сигнала. Двойные соединительные линии указывают на сигналы кадров, и аннотации рядом с линии показывают, что сигналы являются векторами - столбцами соответствующих размеров.

Запуск модели производит следующие изображения. Ваш график количества ошибок мог бы несколько отличаться, в зависимости от вашего значения Initial seed в блоке Random Integer Generator. (Чтобы сделать диапазон координатной оси точно соответствующим диапазону первого изображения, щелкните правой кнопкой мыши на области изображения и выберите Axes properties).

Заметки к методам специфичного блочного кодирования.

Хотя подбиблиотека Block Coding несколько однородна с виду, различные кодирующие методы кодирования не идентичны. Эта секция описывает специальные варианты и ограничения, которые относятся к параметрам и сигналам для категорий методов кодирования в этой подбиблиотеке.

Базовый линейный блочный код.

Кодирование сообщения, использующее базовый линейный блочный код, требует порождающей матрицы. Декодирование требует порождающей матрицы и возможно таблицы истинности. Чтобы использовать блоки Binary Linear Encoder и Binary Linear Decoder, Вы должны знать параметры Generator matrix и Error-correction truth.

Порождающая матрица. Процесс кодирования сообщения в (N, K) линейном блочном коде определяется размера K*N порождающей матрицей G. Определенно, 1* K - мерный информационный вектор v закодирован в 1*N – мерный вектор кодового слова vG. Если G имеет форму [Iк, P] или [P, Iк], где P - некоторая матрица размера K* (N-K) и Iк единичная матрица размеры K*K, G называется стандартной формой. Блоки линейного блочного кодирования в этой библиотеке требуют параметр маски Generator matrix, чтобы быть в стандартной форме.

Декодирующая таблица.

Декодирующая таблица сообщает декодеру, как исправить ошибки, которые, возможно, вносят ошибки в код во время передачи. Коды Хэмминга могут исправить любой однократный ошибочный символ в любом ключевом слове. Другие коды могут исправить, или частично исправить, ошибки больше чем в одном символе в данном кодовом слове.

Блок Binary Linear Decoder позволяет Вам определять декодирующую таблицу в параметре Error-correction truth table. Представьте декодирующую таблицу как матрицу с N столбцами и 2^N-K строками. Каждая строка дает корректирующий вектор для одного полученного вектора кодового слова.

Если Вы не хотите определять декодирующую таблицу явно, установите этот параметр, равным 0. Это заставляет блок вычислять декодирующую таблицу, используя функцию syndtable из Communications Toolbox.

Циклические коды.

Для циклических кодов длина кодового слова N должна быть 2^M-1, где М является целым числом, большим чем или равным 3.

Порождающие полиномы.

Циклические коды имеют специальные алгебраические свойства, которые позволяют иметь полиномы для полного определения процесса кодирования. Этот так называемый порождающий полином степени (N-K) с делителем полинома x^N-1.

Блоки Binary Cyclic Encoder и Binary Cyclic Decoder позволяют Вам определять порождающий полином как второй параметр маски, вместо определения там K. Блоки представляют порождающий полином используя вектор, который перечисляет коэффициенты полинома в порядке возрастания мощности переменных. Вы можете найти порождающие полиномы для циклических кодов используя функцию cyclpoly из Communications Toolbox.

Если Вы не хотите определять порождающий полином, установите второй параметр маски, равным значению K.

Дата добавления: 2014-11-08