Экспериментальные данные и вероятности событий

В конце темы рассмотрим связь между вероятностями случайных событий и экспериментальными статистическими данными. А сделаем это на примере бросания монеты. Будем последовательно, через запятую писать О или Р в зависимости от того, выпал «орел» или «решка». После п бросаний при неизменных условиях этого испытания, у нас в результате получится какая-то случайная последовательность. Например, такая:

О, О, Р, О, Р, Р, О, Р, Р, Р, О, О, Р, О, Р, О, О, Р, Р, О, О, Р...

Иными словами, имеется выборка, в которой две варианты О и Р. Для каждого числа п бросаний монеты можно сосчитать частоту каждой из этих вариант. Сделаем соответствующие расчеты для указанной последовательности.

п

Частота Р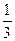

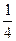
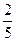
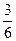
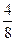
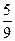
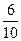
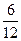
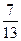
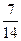
Частота О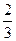

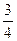
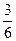
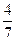
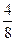
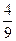
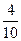
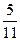
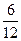
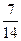
Из таблицы видно, что на 6-м, 8-м, 12-м и 14-м местах частоты обоих вариант равны 0,5. В остальных случаях частоты отличаются от 0,5, но не сильно. На 7-м месте они равны 0,429 и 0,571, а на 13-м месте – 0,538 и 0,462. И с ростом числа бросаний обе частоты все ближе и ближе будут подходить к 0,5. Практическое проведение большого числа экспериментов показывает, что частота выпадения орла при достаточно большом числе бросаний практически неотличима от 0,5. Как уже упоминалось в конце предыдущей темы при п = 24000 эта частота у К. Пирсона получилась равной 0,5005. Итак, при каждом конкретном числе бросаний монеты частота или, как ее называют, эмпирическая частота выпадения герба принимает какое-то конкретное значение. Оно может меняться с изменением числа бросаний. Только вот изменения эти практически незаметны. При достаточно большом числе бросаний частота приближается к некоторому постоянному числу. В данном случае к 0,5. Мы сталкиваемся с замечательным законом природы – статистической устойчивостью.

Определение. При большом числе независимых повторений одного и того же опыта в неизменных условиях частота появления определенного случайного события практически совпадает с некоторым постоянным числом. Это явление называют статистической устойчивостью, а такое число называют статистической вероятностью этого события.

Такая устойчивость имеет место не только при бросании монеты, но и при вытаскивании карт, выпадении определенного числа очков на игральных кубиках, рождении мальчиков, времени восхода солнца и, вообще, для большинства случайных событий. Явление статистической устойчивости соединяет реально проводимые испытания с теоретическими моделями этих испытаний. Приведем несколько примеров, связанных с литературой.

Статистические исследования над большим количеством литературных текстов показали, что частоты появления той или иной буквы (или пробела между словами) стремятся при увеличении объема текста к некоторым определенным константам. Таблицы, в которых собраны буквы того или иного языка и соответствующие константы, называют частотными таблицами языка. Приведем таблицу для букв русского алфавита и пробелов (частоты приведены в процентах).

Буква	А	Б	В	Г	Д	Е	Ж	З	И	Й	К	Л	М	Н	О	П
Частота	6,2	1,4	3,8	1.1	2,5	7,2	0,7	1,6	6,2	1,0	2,8	3,5	2,6	5,3	9,0	2,3
Буква	Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ы	Ь	Э	Ю	Я	–
Частота	4,0	4,5	5,3	2,1	0,2	0,9	0,4	0,4	0,6	0,3	1,6	1,4	0,3	0,6	1,8

Это значит, что из 1000 случайно выбранных в тексте букв или пробелов буква «ф» будет, в среднем, встречаться два раза, буква «о» – девяносто раз, пробел – 175 раз и т. д.

Более того, выясняется, что у каждого автора есть своя частотная таблица использования букв, слов, специфических литературных оборотов и т. п. По этой частотной таблице можно определить автора примерно так же точно, как и по отпечаткам пальцев.

Приведем два примера из нашей недавней истории. До сегодняшнего дня не утихают споры об авторстве «Тихого Дона». Довольно многие считают, что в 23 года М. А. Шолохов такую глубокую и поистине великую книгу написать просто не мог. Выдвигались разные аргументы и разные кандидаты в авторы. Особенно жаркими были споры в момент присуждения М. А. Шолохову Нобелевской премии в области литературы (1965 г.). Статистический анализ романа и сличение его с текстами, в авторстве М. А. Шолохова которых не было сомнений, подтвердил все же гипотезу о М. А. Шолохове, как об истинном авторе «Тихого Дона».

Вторая история носит более политический характер. В середине 60-х годов в одной из стран Западной Европы были опубликованы «очерняющие прогрессивный характер социалистической системы» литературные произведения. Автором был А. Терц и, вне всякого сомнения, это был псевдоним. В соответствующих органах был проведен сравнительный анализ опубликованных «вредительских» текстов и результаты были сличены с произведениями ряда возможных кандидатов в авторы. Ответ оказался однозначным: настоящим автором был литературовед Андрей Донатович Синявский. Он, в общем-то, не отпирался и на суде в 1967 году («Процесс Синявского и Даниэля») получил 5 лет тюрьмы и 7 лет ссылки. Вот такая вот теория вероятностей и математическая статистика.

Контрольные вопросы

1 Что такое математическая статистика? Чем она занимается?

2 Какие величины называют случайными? Когда случайную величину называют дискретной, а когда – непрерывной?

3 Что такое закон распределения дискретной случайной величины? Как он может быть задан?

4 Как задаются непрерывные случайные величины?

5 Что называется генеральной совокупностью, выборкой, вариантой, вариационным рядом?

6 Что такое частота варианты, мода, медиана, размах выборки?

7 Дайте определение математического ожидания случайной величины. Как найти математическое ожидание? Перечислите его свойства.

8 Дайте определение дисперсии случайной величины. Как она находится? Перечислите свойства дисперсии.

9 Что называется статистической устойчивостью и статистической вероятностью случайного события?

Тема 7: Элементы математического моделирования

Модель – это представление объекта, системы или идеи в некоторой форме, отличной от самой целостности.

Дата добавления: 2014-11-16