Непосредственное интегрирование. Таблица основных интегралов

Таблица основных интегралов

Простейшие свойства неопределенного интеграла

I. Постоянный множитель 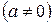можно выносить за знак интеграла:

.

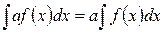II. Интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от слагаемых функций:

.

III. Производная от неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению

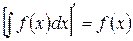или .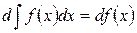

IV. Неопределенный интеграл от дифференциала функции равен сумме этой функции и произвольной 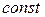, т.е.

или .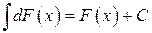

V. Если справедливо равенство 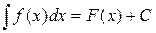, то справедливым будет и соотношение:

.

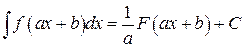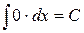
	(1)
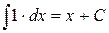
	(2)
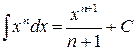
	(3)
	(4)
	(5)
	(6)
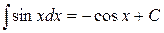
	(7)
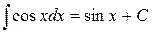
	(8)
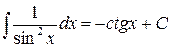
	(9)
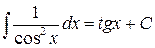
	(10)
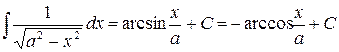
	(11)
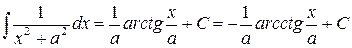
	(12)
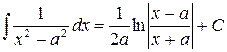
	(13)
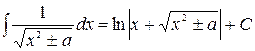
	(14)
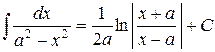
	(15)

Справедливость формул можно проверить путем дифференцирования, т.е. надо убедиться в том, что производные от правых частей формул будут равны соответственно подынтегральным функциям. Так, если 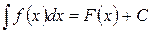, то .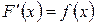

Например, в формуле (14) ; ;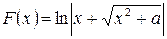

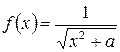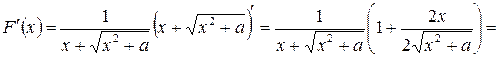
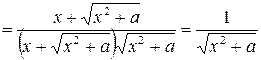, т.е. .

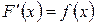Аналогичным способом можно проверить и все остальные формулы. Заметим, что каждая из формул таблицы справедлива в любом промежутке, содержащемся в области определения подынтегральной функции.

Интегралы таблицы называются табличными.

Пользуясь таблицей интегралов и свойствами I, II неопределенного интеграла, можно вычислить многие интегралы.

Пример 1.4.1. Вычислить интеграл .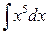

Решение. 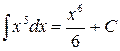. Воспользовались формулой (3).

Пример 1.4.2. Вычислить интеграл .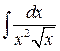

Решение.

. Воспользовались формулой (3).

Пример 1.4.3. Вычислить интеграл .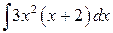

Решение.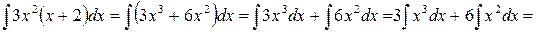

. Воспользовались свойством II и формулами (1), (3).

Пример 1.4.4. Вычислить интеграл .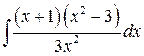

Решение.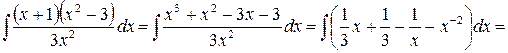

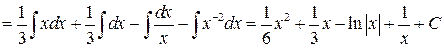. Воспользовались свойством II и формулами (1), (3), (2), (4).

Пример 1.4.5. Вычислить интеграл .

Решение.

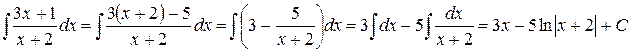Воспользовались свойствами II и I и формулами (2), (4).

Пример 1.4.6. Вычислить интеграл .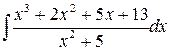

Решение. Подынтегральная функция является неправильной дробью, т.к. степень числителя больше степени знаменателя. Разделив числитель на знаменатель, получим

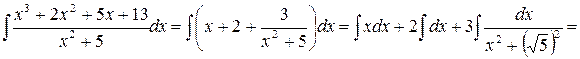
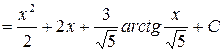. Воспользовались свойствами II и I и формулами (3), (2), (12).

Пример 1.4.7. Вычислить интеграл .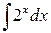

Решение. 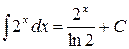. Воспользовались формулой (5).

Пример 1.4.8. Вычислить интеграл .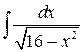

Решение. . Воспользовались формулой (11).

Пример 1.4.9. Вычислить интеграл .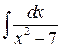

Решение. 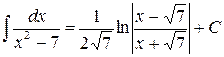. Воспользовались формулой (13).

Пример 1.4.10. Вычислить интеграл .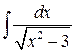

Решение. 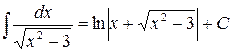. Воспользовались формулой (14).

Пример 1.4.11. Вычислить интеграл .

Решение.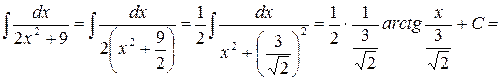

. Воспользовались формулой (12).

Пример 1.4.12. Вычислить интеграл .

Решение. 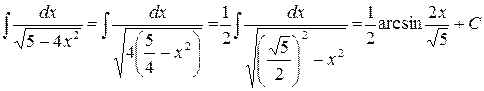. Воспользовались формулой (11).

Пример 1.4.13. Вычислить интеграл .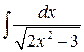

Решение. 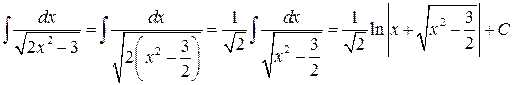. Воспользовались формулой (14).

Пример 1.4.14. Вычислить интеграл .

Решение. 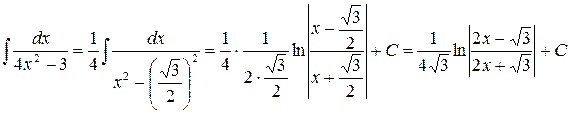. Воспользовались формулой (13).

Пример 1.4.15. Вычислить интеграл .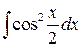

Решение. 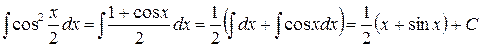. Воспользовались свойствами II и I и формулами (2), (8).

Пример 1.4.16. Вычислить интеграл .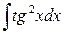

Решение. 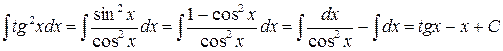. Воспользовались свойством II и формулами (10), (2).

Дата добавления: 2014-11-16