Симметрия кристаллов. Система кристаллов

Классификация кристаллов основана на их симметрии. Тот или иной объект обладает симметрией, если после определенного изме­нения его положения в пространстве он совмещается со своим пер­воначальным положением. Так, трехлопастный пропеллер можно повернуть вокруг оси на 120° (на одну треть оборота), и тогда его положение нельзя отличить от первоначального при условии, что все лопасти совершенно одинаковы.

Рис. 3 Виды симметрии кристалла

Точно так же он может быть повернут на 240° (на две трети оборота), и снова невозможно будет отличить его новое положение от первоначального. Такое вра­щение на одну треть оборота, на две трети оборота, а также пол­ный оборот образуют операции симметрии, характерные для оси симметрии третьего порядка. Некоторые другие примеры симмет­рии показаны на рисунке3.

Кристаллы обладают лишь некоторыми элементами симметрии, к числу которых относятся: центр симметрии, оси симметрии второго порядка, третьего порядка, четвертого порядка, шестого поряд­ка, зеркально-поворотные оси четвертого и третьего порядка, плос­кость симметрии. Все эти виды симметрии показаны на рисунке 4.

Ось симметрии пятого порядка в кристаллах не встречается, по­скольку угол пятиугольника равен 108°, а на такое число не делит­ся угол 360°.

Существует 32 сочетания элементов симметрии, свойственных кристаллам. Эти сочетания называются видами симметрии или классами кристаллов. Описание видов симметрии кристал­лов можно найти в руководствах по кристаллографии. Тридцать два вида (класса) симметрии кристаллов разделяются на шесть систем или сингоний кристаллов:

1) кубическая система (иногда называемая изометрической) с осями симметрии третьего и четвертого порядка (оси четверто­го порядка могут быть зеркально-поворотного типа);

2) тетрагональная система с одной осью четвертого порядка;

3) гексагональная или тригональная система (включает ромбо­эдрические кристаллы) с одной осью шестого порядка или одной осью третьего порядка;

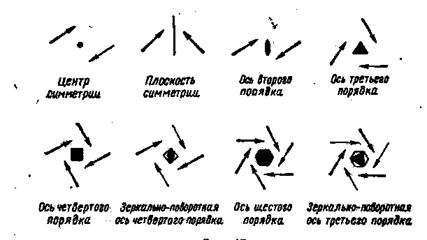
Рис. 4. Виды симметрии кристалла

4) ромбическая система с двумя или тремя плоскостями сим­метрии или осями симметрии второго порядка, образующими прямые углы между собой;

5) моноклинная система с одной плоскостью или одной осью второго порядка, или же с тем и другим элементом симметрии;

6) триклинная система с центром симметрии или без элемен­тов симметрии.

Кристаллы и их элементарные ячейки можно описать осями симметрии, которые в одних случаях могут располагаться под пря­мыми углами одна к другой, в других под углами 120° (в случае гексагональной и тригональной систем), или под другими углами. Различным системам свойственны следующие типы осей:

кубической системе: три равные взаимно перпендикулярные оси длиной а;

тетрагональной системе: две равные оси длиной а и третья ось длиной с; все оси взаимно перпендикулярны;

гексагональной или тригональной системе: две равные оси дли­ной а образуют между собой угол 120°, третья ось длиной с распо­ложена под прямым углом к первым двум:

ромбической системе: три оси длиной соответственно а, b, с, рас­положенные взаимно перпендикулярно;

моноклинной системе: две оси (а и с) образуют между собой угол β, а третья ось b расположена под прямым углом к осям а и с;

триклинной системе: три оси а, b и с образуют между собой углы α, β и γ.

Между гранями кристалла и осями должны существовать ра­циональные отношения: отрезки осей, отсекаемых гранью, относятся к длинам осей а, b и с, как простые числа. Схематическое изобра­жение осей кристаллов и граней показано на рисунках 5 и 6.

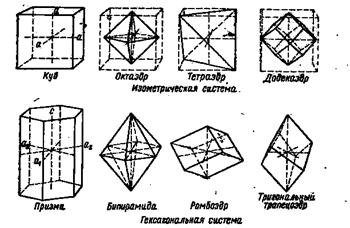
Рис. 5. Схематическое изображение осей кристаллов и граней

Дата добавления: 2014-11-16