Общие сведения. Matlab является компьютерной системой, которая предназначена для осуществления операций с матрицами

РАБОТА С МАТРИЦАМИ В MATLAB

Matlab является компьютерной системой, которая предназначена для осуществления операций с матрицами. Матрица, столбец, строка – это математические объекты. Способом их представления и хранения в памяти компьютера является массив (Array). По умолчанию в Matlab принято, что любая заданная переменная представляет собой массив. Под матрицей понимается двумерный массив 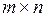, под вектором – одномерный: 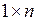– вектор-строка или 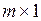– вектор-столбец. Отдельно заданное значение (скаляр) Matlab воспринимает как массив размером 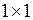. В программировании массив это совокупность однотипных значений, упорядоченных по индексам. У массива, как и у любой переменной, должно быть имя. Все элементы одного массива имеют одинаковое имя – имя массива и различаются порядковыми номерами (индексами). Индексы однозначно определяют положение элемента в массиве.
В Matlab разрешены только натуральные индексы. Все элементы массива одинаково доступны. Для инженера больший интерес представляет сам объект – матрица, нежели способ его хранения – массив. Поэтому в дальнейшем будут преимущественно использоваться слова "матрица" и "вектор". Для обозначения матриц в математическом тексте принято использовать прописные, а для векторов строчные полужирные буквы прямого шрифта. Для их отдельных элементов – буквы строчного курсива. Например, 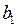– первый элемент вектора b, 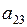– элемент матрицы А, стоящий во второй строке в третьем столбце (рис. 2.1, а). В памяти компьютера Matlab хранит матрицу по столбцам (рис. 2.1, б). Это может быть важным при выполнении операций над матрицей и адресации отдельных ее элементов.

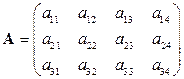
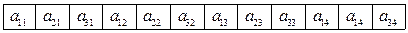
а б

Рис. 2.1. Матрица А и ее представление в памяти

2. Одномерные массивы – векторы

Для определенности будем рассматривать числовые данные. Векторы – это линейные наборы чисел (элементов), в которых позиция каждого элемента задаётся единственным числом – его номером. Можно говорить о первом элементе вектора, о втором и т.д. Matlab различает прописные и строчные буквы. Поэтому в тексте программы или в командной строке и вектор в целом, и отдельный его элемент обозначаются одними и теми же символами. Элемент отличается тем, что за его именем обязательно стоит индекс, заключенный в круглые скобки. В общем случае индекс может быть вычисляемым объектом, т.е. задаваться выражением.

Для создания вектора, состоящего из нескольких чисел, чаще всего используется операция конкатенации (сцепления, объединения), обозначаемая в Matlab с помощью квадратных скобок – [ ]. Элементы, объединяемые в массив, должны отделяться друг от друга разделителями. При формировании вектора-строки в качестве разделителя можно использовать пробел и/или запятую. Например, выражение

>> a=[1 2 3]

a =

1 2 3

формирует переменную с именем a, являющуюся вектором-строкой из трёх чисел. Поскольку в конце командной строки не поставлен символ подавления эхо-печати – точка с запятой, то после нажатия на Enter на экране распечатался результат выполнения команды – содержимое созданной переменной с именем а (строки результата не предваряются символом >>). Из результата хорошо видно, что а именно вектор-строка. Аналогичный результат можно получить, выполнив выражение

>> b=[10,20,30]

b =

10 20 30

В этом примере разделителем элементов при формировании вектора являлась запятая. Можно одновременно использовать оба разделителя, или задавать значения элементов через несколько пробелов. Вектор можно формировать и поэлементно (прописать каждый элемент отдельно, не используя конкатенацию). Например

>> c(1)=1.5; c(2)=2*c(1)

c =

1.5000 3.0000

В первой строке примера сформирован вектор с из двух элементов, причем второй имеет в двое большее значение, чем первый. Во второй и третьей строках дано эхо Matlab – печать результата. После выполнения этих примеров в рабочем пространстве будут размещены три переменные с именами a, b и с (рис. 2.2).

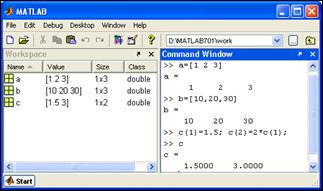
Рис. 2.2. Создание векторов-строк

В колонке Size рабочего пространства Workspace хорошо видно, что созданы именно векторы-строки – для них указаны размеры типа 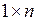. Теперь можно корректировать значения элементов созданных переменных, добавлять в них новые элементы, объединять векторы (конкатенировать). Например

>> a(3)=13; a(4)=4

a =

1 2 13 4

>> b=[b 4.25]

b =

10.0000 20.0000 30.0000 4.2500

>> c=[7.5 c a]

c =

7.5000 1.5000 3.0000 1.0000 2.0000 13.0000 4.0000

В векторе a изменили значение третьего элемента со старого, равного 3, на новое, равное 13, и добавили четвертый элемент. К вектору b тоже добавили четвертый элемент, равный 4,25, но технологией конкатенации. В начало вектора с добавлен элемент (уже имеющиеся элементы автоматически сдвинулись вправо на один индекс), а в его конец ("в хвост") конкатенированы элементы вектора a (сам вектор а при от этого не изменяется). Вектор с стал длиной 7 элементов.

Текущую длину одномерного массива (количество элементов в нем) всегда можно узнать с помощью функции length (длина)

length(с)

ans =

Векторы могут состоять не только из вещественных чисел. Выражение

d = [1+2j, 2+3j, 3-4j];

формирует вектор-строку d из трех комплексных чисел.

Выражение

>> d = [];

сделает вектор пустым (переменная d сохранится в Workspace, но размер ее будет 0×0).

>> с=[ [] 3]

с =

сначала очистит переменную с (сделает вектор пустым), а потом добавит в нее первый (и он будет единственный) элемент, равный 3.

Внимание: 1. При попытке адресации несуществующего элемента, например пятого элемента вектора a, в командном окне Matlab появится сообщение об ошибке

>> a(5)

??? Index exceeds matrix dimensions.

извещающее, что указанный в выражении индекс превысил размер матрицы (в данном случае имеется в виду матрица из одной строки). В то же время запись несуществующего элемента слева от оператора присваивания вполне допустима – она означает добавление нового элемента к уже существующему вектору

>> a(5) = -17;

2. Добавление в пустой или не еще существующий вектор элементов с номерами, идущими с пропуском значений, породит заполнение нулями не адресованных элементов вектора.

> d=[];

>> d(3)=3; d(7)=17

d =

0 0 3 0 0 0 17

В результате в векторе d будет семь элементов.

Для задания значений компонентов вектора-столбца используются те же приемы, но в качестве разделителей элементов выступает символ ";" – точка с запятой. Например

>> a=[1; 5; 10]

a =

>> b=[2 4]'

b =

>> c=[a; b]

c =

>> d=[6

9]

d =

Здесь вектор b получается из вектора-строки при помощи операции транспонирования, обозначаемой символом ' (апостроф). Вектор с формируется конкатенацией двух столбцов a и b. При формировании столбца d в качестве разделителя элементов используется признак конца строки (нажатие на Enter). В результате четырех операций присваивания в рабочем пространстве (рис. 2.3) будет сформировано четыре вектора-столбца (в колонке Size размер переменных указан по типу 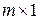– столбец из m строк и в колонке Value значения компонентов перечислены хоть и в строку, но через точку с запятой). Тип (класс) элементов у всех векторов double – числовой двойной точности.

Рис. 2.3. Векторы-столбцы в Workspace

3. Двумерные массивы – матрицы

Сказанное ранее о векторах справедливо и для матриц. Матрицу можно рассматривать как вектор-столбец из векторов-строк и задавать в командной строке

>> a=[1 2 3; 4 5 6]

a =

1 2 3

4 5 6

или как вектор-строку из векторов-столбцов

>> a=[[1; 4] [2; 5] [3; 6]]

a =

1 2 3

4 5 6

или вводить "классическим" способом – строку за строкой, нажимая после элементов каждой строки на Enter

>> a=[1 2 3

4 5 6]

a =

1 2 3

4 5 6

Во всех трех случаях результат одинаков. У элемента матрицы два индекса, которые указываются в круглых скобках: первым – номер строки, вторым через запятую – номер столбца, на пересечении которых стоит элемент. Отдельный элемент матрицы (как впрочем, и вектора) может использоваться в выражениях наравне со скалярами. Например, используя элементы введенной выше матрицы а 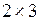, можно вычислить значение 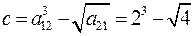следующим образом:

>> c=a(1,2)^3-sqrt(a(2,1))

c =

Индекс может быть и вычисляемым (задаваться выражением)

>> m=2; n=m+1;

>> a(m-1,n)

ans =

Добавить к существующей матрице строку или столбец можно конкатенацией. Например

>> b=[7 8 9]

7 8 9

>> a=[a; b]

a =

1 2 3

4 5 6

7 8 9

Внимание: размер добавляемой строки (столбца) должен совпадать с соответствующими размерами матрицы. В противном случае будет зафиксирована ошибка. Например

>> a=[a; [1 2 3 4]]

??? Error using ==> vertcat

All rows in the bracketed expression must have the same number of columns.

Этим сообщением Matlab извещает, что ошибочно используется вертикальная конкатенация. Все строки в выражении, заключенном в скобки, должны иметь одинаковое число столбцов. По аналогии можно выполнять и конкатенацию матриц. Например, горизонтальная конкатенация матриц (по столбцам)

>> a1=[1 2 3; 4 5 6]

a1 =

1 2 3

4 5 6

>> a2=[11 12 13 14; 15 16 17 18]

a2 =

11 12 13 14

15 16 17 18

>> a=[a1 a2] % матрицы с одинаковым числом строк

a =

1 2 3 11 12 13 14

4 5 6 15 16 17 18

Вертикальная конкатенация матриц (по строкам)

>> b1=[1 2 3; 4 5 6; 7 8 9]

b1 =

1 2 3

4 5 6

7 8 9

>> b2=[11 12 13; 14 15 16]

b2 =

11 12 13

14 15 16

>> b=[b1; b2] % матрицы с одинаковым числом столбцов

b =

1 2 3

4 5 6

7 8 9

11 12 13

14 15 16

Текущий размер матрицы – число строк и столбцов – можно определить с помощью функции size (размер)

>> a=[1 2; 3 4; 5 6]

a =

1 2

3 4

5 6

>> size(a)

ans =

3 2

В ответе первым указывается число строк, вторым – число столбцов матрицы. Результат работы функции size (как и любой другой функции) можно сохранить в переменных и в дальнейшем использовать. По правилам языка слева от оператора присваивания может стоять имя только одной переменной. Например, можно записать

>> s=size(a)

s =

3 2

Из эхо-печати результата видно, что переменная s будет вектором-строкой, первый элемент которой равен числу строк матрицы а, второй – числу ее столбцов. И если требуется использовать в вычислениях, например, число строк матрицы, то в тексте программы необходимо указать s(1) – первый элемент вектора. Применять переменные с индексом не всегда комфортно. Удобнее было бы иметь две скалярные переменные – отдельные число строк и число столбцов. Ситуацию можно разрешить несколькими способами. Можно поэлементно разнести массив по скалярам

>> numrow=s(1)

numrow =

>> numcol=s(2)

numcol =

А можно "обмануть" Matab – разместить результат в два скаляра, конкатенированных вектор

>> [numrow numcol]=size(a)

numrow =

numcol =

Формально правила языка не нарушены, слева от знака = указан один объект – вектор, но только задан он не именем переменной, как обычно. Красиво! И, конечно же, никакого обмана здесь нет! Такая конструкция выражения присваивания официально используется в Matlab при работе с функциями, возвращающими несколько значений (и даже больше двух, и даже разных типов). Пример является поучительным, поскольку прием конкатенации отдельных переменных и/или констант в вектор часто используется в Matlab в случаях, когда необходимо разместить несколько объектов, а разрешен только один.

Сделать матрицу любого размера пустой можно одной операцией присваивания

>> b=[];

>> size(b)

ans =

0 0

Внимание: "пустая матрица" не значит "несуществующая"! Имя пустой матрицы b сохраняется в Workspace и в дальнейшем может использоваться для формирования матрицы любого размера, в том числе и 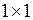, т.е. скаляра.

Дата добавления: 2014-11-08