Поэлементные и матричные операции

Ранее было отмечено, что Matlab представляет числа в виде массива 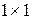. Отсюда следует, что для операций над векторами и матрицами можно использовать те же знаки операций, что и для скалярных данных. Так, например, сложить два вектора одной размерности можно при помощи обычного "+"

>> x=1:4

x =

1 2 3 4

>> y=10:10:40

y =

10 20 30 40

>> z=x+y

z =

11 22 33 44

Векторы складываются поэлементно 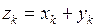, , 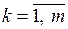где т – длина суммируемых векторов. В результате сумма является вектором того же размера, что и векторы-слагаемые. Аналогично и для матриц. Сумма (разность) двух матриц равна матрице, каждый элемент которой есть сумма (разность) соответствующих элементов матриц-слагаемых размером 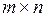: 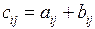, , 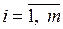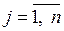. Поэлементно можно применять к массивам элементарные математические функции (см. табл. 1.4), операции отношения и логические операции (см. табл. 1.5). Например, вычислить значени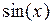я для 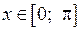с шагом 30° можно следующим образом:

>> x=0:pi/6:pi;

>> y=sin(x)

y =

0 0.5000 0.8660 1.0000 0.8660 0.5000 0.0000

Поскольку х – вектор-строка, то у будет вектором того же размера, что и х.

С операциями типа "умножение" (возведение в степень, умножение и деление) несколько сложнее. Дело в том, что в Matlab имеется два различных типа арифметических операций типа "умножение" – поэлементные и для массивов в целом (матричные). Матричные арифметические операции определяются правилами линейной алгебры. Например, поэлементное умножение матриц A и B размером 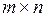выполняется в соответствии с равенством: 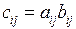, , 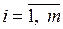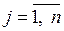. Матрицы-сомножители при таком умножении должны быть одно размера. Матричное же умножение двух матриц возможно только в том случае, когда число столбцов первой матрицы равно числу строк второй. Произведением матрицы А размером 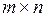на матрицу B размером 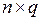является матрица с размером 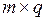, каждый элемент i -ой строки и k -го столбца которой равен сумме локальных произведений соответственных элементов i -ой строки матрицы А и k -го столбца матрицы B: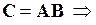 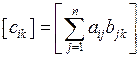, , 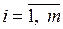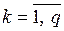. В общем случае умножение матриц не коммутативно, т.е. ab ≠ ba. Возведение матрицы в целую степень р возможно только для квадратных матриц. Если р – положительное целое, то А ^р эквивалентно умножению матрицы А саму на себя р раз. Операция вычисления матрицы а ^–1, называемая обращением матрицы а, возможна только для квадратной матрицы с определителем, не равным нулю. Если р – отрицательное целое, то А ^р эквивалентно умножению обратной матрицы саму на себя р раз.

Знак точки ". " отличает операции над элементами массивов от матричных операций. Сравните

A1=[2 3; 4 5]; A2=[1 4; 6 2]; %задаются матрицы 2×2

A3=a1*a2 % матричное умножение матриц

A3 =

20 14

29 28

A4=a1. *a2 % поэлементное умножение матриц

A4 =

2 12

30 8

Символ "%" отделяет комментарий (пояснительный текст) от команд.

>> a=[1 2 3; 0 4 5] % задается матрица 2×3

a =

1 2 3

0 4 5

>> a.^2 %поэлементное возведение в квадрат

ans =

1 4 9

0 16 25

>> a^2 %матричное возведение в квадрат

??? Error using ==> mpower

Matrix must be square.

Попытка возвести в квадрат прямоугольную матрицу 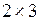вызвала ошибку использования матричного произведения с сообщением "Матрица должна быть квадратной".

Примеры наглядно демонстрируют, что для одних и тех же матриц результаты поэлементных и матричных операций типа "умножение" разные! Арифметические операции типа "сложение" над массивами всегда выполняются поэлементно, поэтому операции ". +" и ". -" не существуют.

В математике не определена операция деления матриц и векторов. Но в Matlab символы / и \ используются для решения матричных уравнений. Операция b/a эквивалентна операции b*inv(a), где функция inv осуществляет обращение матрицы. Эту операцию удобно использовать для решения матричного уравнения 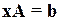. Операция а\b равносильна операции inv(a)*b, которая представляет собой решение матричного уравнения 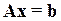. При помощи оператора / можно поделить вектор или матрицу на число. Например

>> v=4:2:10

v =

4 6 8 10

>> w=v/2

w =

2 3 4 5

Попытка поделить число на вектор или матрицу вызовет ошибку

>> q=2/v

??? Error using ==> mrdivide

Matrix dimensions must agree.

Matlab сообщает об ошибке использования матричного деления. Размеры матриц должны быть согласованы.

А вот операция поэлементного деления пройдет в обоих
случаях.

>> q=2./v

q =

0.5000 0.3333 0.2500 0.2000

Здесь значение 2 было поочередно поделено на каждый из элементов вектора v. И каждый из элементов вектора может быть поделен на 2

>> w=v./2

w =

2 3 4 5

Из примеров видно, что при делении или умножении вектора (матрицы) на скаляр поэлементные операции не отличаются от матричных

>> w=v/2

w =

2 3 4 5

т.е. точку перед знаком операции в этих случаях ставить не обязательно.

Дата добавления: 2014-11-08