Двумерная графика

Построение таблицы значений функции

Отображение результатов в виде таблицы удобно, если имеется сравнительно небольшое количество значений функции. Пусть требуется вывести в командное окно таблицу значений функции 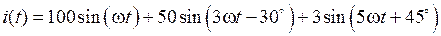, представляющей собой аналитическое описание полигармонического сигнала, состоящего из первой, третьей и пятой гармоник базовой частоты 50 Гц), для моментов времени 0; 0,003; 0,01; 0,015; 0,02; 0,027; 0,03; 0,034; 0,04. Технология табулирования функции в Matlab состоит в реализации следующих шагов:

1. Создадим вектор-строку, содержащую значения независимой переменной (данном примере это время). Соблюдая правила хорошего тона, дадим ей мнемоническое имя t – время;

2. Вычислим значения тока для каждого элемента вектора t и разместим их в векторе-строке с именем current – ток. При вычислениях для упрощения выражений рекомендуется использовать промежуточные переменные. Так, в нашем примере удобно ввести переменную w=100*pi, соответствующую частоте 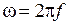. Следует помнить, что операции в выражении для вычисления значений функции должны выполняться поэлементно;

3. Придадим таблице более удобный для чтения вид. Как правило, данные в таблице располагают в столбцах. Таблица предваряется названием и шапкой. Для оформления шапки таблицы обычно используется функция disp, предназначенная для вывода значений в командное окно Matlab.

Реализуем шаги описанной выше технологической цепочки табулирования функции в программе на языке Matlab, оформленной в виде script-файла tabfun.m (рис. 4.1).

Рис. 4.1. Окно редактора с текстом script-файла

В титульной строке окна редактора видно, что данный файл сценария сохранен на диске D в каталоге MATLAB701 в папке work. В нижней части окна редактор отмечает, что данный m-файл является именно скриптом. По левой стороне окна даны номера строк программы. Matlab будет на них ссылаться при обнаружении ошибок в тексте программы (синтаксические ошибки) или при ее выполнении (ошибки шага выполнения). В целом окно редактора оформлено в привычном стиле Windows. На рис. 4.2 показано как выполнение этой программы отразилось на состоянии рабочего стола.

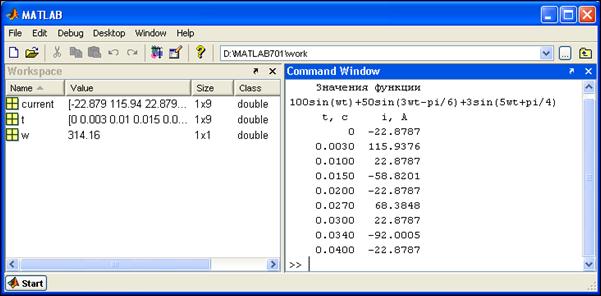
Рис. 4.2. Результат выполнения программы рис. 4.1

В рабочем пространстве Workspace созданы три переменные, содержащие по девять расчетных значений тока, времени и скаляр частоты. Эти данные могут быть использованы в дальнейшем, как обычные переменные Matlab (каковыми они и являются). В командном окне отображена таблица из двух колонок. Первая – время, вторая – значения тока для заданных моментов времени.

Двумерная графика предназначена для построения на плоскости графиков функций одной переменной (одного аргумента) 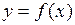. Список функций, используемых в двумерной графике, может быть выведен в Command Window по команде

help graph2d

3.1. Общие правила построения графиков

функции одной переменной

Общие правила задания графиков следующие:

1) размеры х и у должны быть согласованы;

2) если х и у – векторы, то будем иметь один график функции ;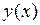

3) если х – матрица, а у – вектор, то будем иметь графики функции 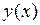, аргументы которой заданы столбцами матрицы х;

4) если х – вектор, а у – матрица, то будем иметь графики функций, заданных столбцами матрицы у, одного аргумента х;

5) если х и у – матрицы, то будем иметь графики функций, заданных столбцами матрицы у, аргументы которых заданы столбцами матрицы х.

Общие правила вывода графиков следующие:

1) текущий график, строится с помощью одной из специальных функций Matlab в текущем графическом окне Figure 1 (рис. 4.3). По умолчанию очередной график выводится в то же окно, при этом предыдущий график автоматически удаляется. Интерфейс графического окна соответствует стилю Windows: содержит титульную строку, стандартную строку меню, панель инструментов, которые легко осваиваются интуитивно;

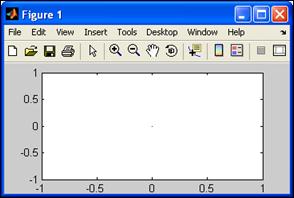
Рис. 4.3. Пустое графическое окно

2) открытие отдельного графического окна с номером n для вывода в него очередного графика выполняется по команде
figure(n), которая ставится перед обращением к очередной функции построения графика;

3) режим наложения графиков (вывод в текущее графическое окно нескольких графиков в одних осях), строящихся с помощью отдельных функций Matlab, обеспечивается командой hold on, которая ставится перед очередной функцией построения графика;

4) отмена режима наложения графиков выполняется командой hold off, которая ставится после последней функции построения графика в текущем окне;

5) разбиение текущего графического окна на подокна для вывода в них независимых графиков выполняется с помощью функции subplot(m,n,p). Здесь m и n – соответственно количество строк и столбцов в матрице подокон; р – порядковый номер текущего (активного) подокна, считая по строкам слева направо.

3.2. Оформление графиков

Основные функции оформления графиков функций приведены в табл. 4.1.

Таблица 4.1

Функция	Описание	Формат использования
axis	Управление масштабированием по осям	axis auto – автоматическое масштабирование осей (установлено по умолчанию); axis square – построение в квадратной области; axis equal – построение с равным шагом по обеим осям; axis off – удаление изображения осей координат и надписей на них; axis ij – перемещает начало отсчета в левый верхний угол; axis xy – возвращает декартову систему координат с началом отсчета в левом нижнем углу графика.
grid	Нанесение координатной сетки с автоматическим выбором шага	grid
gtext	Вывод текста на поле графика в произвольном месте	gtext(' текст ') Начало текста указывается на поле графика перекрестием и может перемещаться мышью
legend	Размещение легенды	legend(' текст 1',' текстN ',pos) где текст i – названия графиков, изображенных в одних осях; pos – параметр размещения легенды: -1 – вне поля графика, 0 – автоматическое расположение, 1 или 2 – в правом или левом верхнем углу, 3 или 4 – в правом или левом нижнем углу
title	Вывод заголовка графика	title(' текст_заголовка ')
xlabel ylabel	Обозначение осей абсцисс и ординат соответственно	xlabel(' текст ') ylabel(' текст ')
xlim ylim	Установка границ по оси абсцисс и ординат при выводе графика	xlim([xmin xmax]) ylim([ymin ymax]) Двухэлементные векторы задают границы по соответствующим осям

3.3. Построение графиков

Matlab позволяет строить графики функций в линейном, логарифмическом и полулогарифмическом масштабах. В одном графическом окне можно построить графики нескольких функций, с разным шагом и даже определенных на разных отрезках. В последнем случае при построении графиков Matlab выбирает максимальный отрезок, содержащий все остальные. Дополнительные параметры графических функций позволяют управлять основными свойствами линий на графиках. Для того чтобы построить график функции, нужно сформировать два вектора x (абсцисс) и y (ординат) одинакового размера и обратиться к соответствующей функции рисования. Таким образом, фактически строится график таблично заданной функции, т.е. зависимость одного вектора от другого. Поведение функции между узлами таблицы определяется линейной интерполяцией, т.е. соседние точки соединяются прямой линией. Наиболее часто используемые функции Matlab, предназначенные для построения двумерных графиков, приведены в табл. 4.2.

Таблица 4.2

Функция	Формат использования	Назначение
plot	plot(x,y)	График в линейном масштабе
plotyy	plotyy(x,y)	График в линейном масштабе с двумя осями ординат
loglog	loglog(x,y)	График в логарифмическом масштабе по обеим осям
semilogx	semilogx (x,y)	График в логарифмическом масштабе по оси абсцисс и линейном по оси ординат
semilogy	semilogx (x,y)	График в линейном масштабе по оси абсцисс и логарифмическом по оси ординат
fplot	fplot(' функция ',[d1 d2], tol, n)	График на заданном интервале с автоматическим выбором шага. Эта функция будет рассмотрена позднее в работе ИП5

Рассмотрим использование этих функций более подробно. Построение графиков функций одной переменной в линейном масштабе осуществляется при помощи функции plot. В зависимости от входных аргументов plot позволяет строить один или несколько графиков, менять цвет и стиль линий и добавлять маркеры на каждый график. В простейшем случае обращение к функции может быть выполнено с одним аргументом

plot(y)

Здесь y – вектор или матрица значений функции. В качестве значений аргумента в этом случае будут служить индексы элементов вектора или столбцов матрицы.

В классическом варианте функция вызывается с двумя

plot(x,y)

или тремя аргументами

plot(x,y,options)

Здесь x и y – векторы, элементами которых являются значения аргумента и функции соответственно; options – список опций управления свойствами линии графика, заключенный в апострофы. Список опций может содержать до трех специальных символов, определяющих тип линии, тип маркера и цвет линии графика (табл. 4.3).

Таблица 4.3

Тип линии	Тип маркера	Цвет линии (маркера)
- непрерывная	. точка	b синий
-- штриховая	+ плюс	g зеленый
: пунктир	* звездочка	r красный
-. штрих-пунктир	о кружок	с голубой
х крестик	m фиолетовый
s квадрат	у желтый
d ромб	k черный
	v треугольник вниз
	< треугольник влево
	> треугольник вправо
	p пентаграмма
	h шестиугольник

За одно обращение к plot можно нарисовать и несколько графиков в одних осях. Например, три графика можно нарисовать следующим образом:

plot(x1,y1,x2,y2,x3,y3)

или

plot(x1,y1,'--og',x2,y2,'k-.+',x3,y3,'*:k')

или

plot(x1,y1,x1,y2,'-r',x3,y3,'om')

Из примеров видно, что в одних осях можно рисовать графики, как для одинаковых, так и для разных значений аргументов; некоторым кривым можно задавать опции рисования, а некоторым – нет; можно задавать как полный список опций, так и частичный; перечислять опции можно в любом порядке. По умолчанию (список options не указан) график строится непрерывной линией, тип маркера – точка (пиксель), цвет – в зависимости от того, какая по порядку кривая отображается при обращении к данной функции. Порядок автоматического перебора цветов соответствует их перечислению в табл. 4.3. Если одним plot рисуется больше восьми графиков, то цвета начинают циклически повторяться.

Рекомендации: 1) если в графическом окне необходимо показать, что один график совпадает с другим, то первый из них следует рисовать сплошной линией одного цвета, а второй – прерывистой линией другого цвета. Иначе на экране будет виден только график, нарисованный последним!

2) Если расчетных точек много, то не стоит прорисовывать маркеры. Иначе на экране будет изображена "гусеница" – сплошной поток маркеров. Если маркеры все же необходимы, то следует нарисовать не все, а только некоторые из них. Например, каждый десятый или каждый сотый маркер. Для этого отдельно с более крупным шагом формируются векторы значений функции и аргумента

markx=x(1:100:end); marky=y(1:100:end);

которые затем используются для прорисовки маркеров поверх уже нарисованной кривой, изображающей функцию

plot(x,y,markx,marky,'o')

Выше говорилось о том, что при рисовании графиков plot автоматически выполняет линейную интерполяцию между соседними точками. Об этом необходимо помнить, задавая количество точек при изображении кривых. Иначе можно получить "фантастический" результат! Например, пусть требуется построить график функции 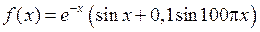на отрезке [0; 0,2]. Напишем программу, не забывая, что табулирование функции выполняется поэлементными операциями над векторами. Сохраним программу в m-файле (впрочем, эта программа хороша и для выполнения в режиме прямых вычислений).

x1=0:1e-2:0.2;

y1=exp(-x1).*(sin(x1)+0.1*sin(100*pi*x1));

x2=0:0.7e-2:0.2;

y2=exp(-x2).*(sin(x2)+0.1*sin(100*pi*x2));

x3=0:0.1e-2:0.2;

y3=exp(-x3).*(sin(x3)+0.1*sin(100*pi*x3));

plot(x1,y1,'r--',x2,y2,'b',x3,y3,'k-.'), grid

title('y=e^-^x(sin(x)+0,1sin(100pi*x)')

xlabel('x'), ylabel('f(x)')

legend('not correct curve1','not correct curve2','correct curve3')

Выполним программу. Откроем графическое окно (рис. 4.4). Видим, что графики y1(x1), построенный пунктиром с шагом 0,01, и y2(x2), построенный сплошной линией с шагом 0,07, просто неверные! А вот третий график y3(x3), нарисованный с шагом 0,001 штрих-пунктиром, соответствует действительности. В чем же дело? Почему одна и та же функция нарисована до неузнаваемости по-разному? Ответ прост – в первых двух случаях вычисления со слишком большим шагом привели к тому, что расчетные точки, верные сами по себе, легли на синусоидоподобной кривой функции неудачно и, соединенные между собой отрезками прямой, исказили ее изображение.

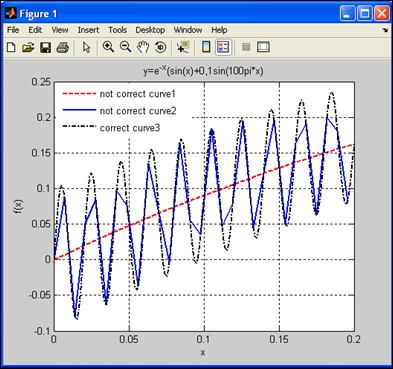
Рис. 4.4. Графики функции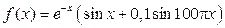

Иногда требуется сравнить поведение двух функций, значения которых сильно отличаются друг от друга. При рисовании автоматически будет выполнено масштабирование. В результате график функции с небольшими значениями практически сольется с осью абсцисс, и установить его вид будет затруднительно.

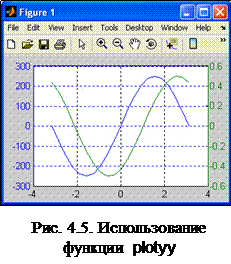Выход может быть найден в использовании функции plotyy, которая выводит графики в окно с двумя осями ОУ, имеющими подходящий масштаб. При этом цвета графика и соответствующей ему оси ординат будут совпадать. На рис. 4.5 приведен результат выполнения в режиме прямых вычислений следующей последовательности операторов:

>> x=-pi:pi/10:pi;

>> y1=250*sin(x);

>> y2=0.5*sin(x-pi/3);

>> plotyy(x,y1,x,y2), grid

Функцию plotyy можно использовать только для рисования двух кривых в одних осях. При построении большего числа разновеликих функций можно воспользоваться домножением вектора ординат на масштабный множитель. Например, задать растяжение первой и сжатие второй кривых по вертикали в сто раз

plot(x,100*y1,x2,0.01*y2,x,y3)

Факт принудительного масштабирования кривых обязательно следует отразить в легенде

legend('100у1(х)','0,01у2(х)','y3(x)')

Функции plot и plotyy используют при построениях линейный масштаб по обеим осям. Для построения графиков в логарифмическом и полулогарифмическом масштабах служат функции loglog, semilogx и semilogy (см. табл. 3.3). Аргументы и правила использования этих функций такие же, как и для функции plot.

При построении графиков бывает удобно задавать векторы значений аргументов x, используя следующие функции:

linspace(d1,d2,n) – задание диапазона по оси абсцисс в линейном масштабе. Здесь d1, d2 – начальное и конечное значения диапазона; n – количество равноотстоящих точек (по умолчанию 50);

logspace(d1,d2,n) – задание диапазона по оси абсцисс в логарифмическом масштабе. Здесь d1, d2 – начальное 10^d1 и конечное 10^d2 значения диапазона; n – количество точек в логарифмическом масштабе (по умолчанию 50).

3.4. Управление свойствами графиков

Свойствами графиков можно управлять с помощью дополнительных (необязательных) входных параметров функций построения графиков, которые разделены на две группы: LineSpec – свойства без стандартных имен и PropertyName – свойства со стандартными именами. Параметры группы LineSpec представлены тремя разновидностями: тип линии, цвет линии и тип маркеров. В функциях построения графиков они задаются в апострофах без разделительных символов и в произвольном порядке. Параметры этой группы были рассмотрены в табл. 4.3.

Параметры группы PropertyName представлены четырьмя разновидностями со следующими стандартными именами (задаются в апострофах):

LineWidth – толщина линии в пунктах (1 пункт = 1/75 дюйма ≈ 0,34 мм), задаваемая числом (по умолчанию равна 0,5);

MarkerEdgeColor – цвет маркера, задаваемый так же, как и цвет линии (см. табл. 4.3). По умолчанию цвет маркера совпадает с цветом линии;

MarkerFaceColor – цвет заливки маркера, задаваемый так же, как и цвет линии (см. табл. 4.3). По умолчанию маркер не закрашивается (прозрачный);

MarkerSize – размер маркера в пунктах, задаваемый числом (по умолчанию равен 7).

Параметры для маркера сработают, если соответствующий параметр LineSpec установил тип маркера. Если функция рисования используется с параметрами, задаваемыми стандартными именами, то она может отображать только одну кривую. Для прорисовки нескольких кривых в одних осях необходимо включить режим наложения. Например

>> x=linspace(-pi,pi,50);

>> y1=100*sin(3*x);

>> y2=100*sin(x)+50*cos(5*x);

>> hold on

>> plot(x,y1,'rs--','LineWidth',2,'MarkerSize',5)

>> plot(x,y2,'bo--','LineWidth',1.5,'MarkerFaceColor','y')

>> title('Графики функций в режиме наложения')

>> grid, legend('y1=100sin(3x)','y2=100sin(x)+50cos(5x)')

>> hold off

Результат работы программы приведен на рис. 4.6.

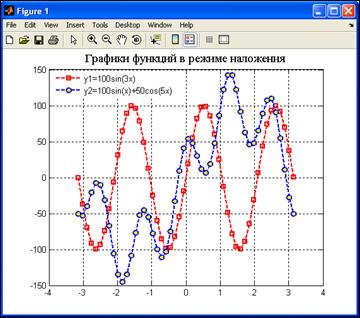
Рис. 4.6. Графики двух функций, построенные в режиме наложения

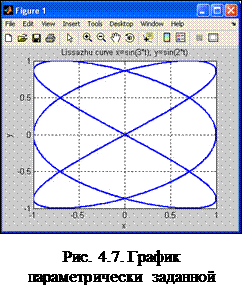С помощью plot можно строить и графики параметрически заданных функций. Для этого сначала генерируется вектор значений аргумента. Затем вычисляются значения функции и записываются в векторы, которые и используются в качестве аргументов plot. Например, на рис. 4.7 показана одна из фигур Лиссажу, построенная при выполнении следующей программы:

>> t=-2*pi:1e-2:2*pi;

>> x=sin(3*t);

>> y=sin(2*t);

>> plot(x,y), grid

>> xlabel('x'), ylabel('y')

>> title('Lissazhu curve x=sin(3*t); y=sin(2*t)')

Для построения специальных двумерных графиков в Matlab используются функции, приведенные в табл. 4.4. Основные правила использования этих функций такие же, как и для plot. Свойства графиков также могут быть заданы параметрами управления LineSpec и PropertyName. Палитра цветов построения диаграмм и гистограмм могут быть заданы с помощью функции colormap (см. разд. 4.3).

Таблица 4.4

Функция	Назначение	Формат
stem	Решетчатая функция	stem(y) stem(x,y)
stairs	Ступенчатая функция	stairs(y) stairs(x,y)
polar	График комплексной функции в показательной форме в полярных координатах	polar(phi,r)
compass	Векторы в алгебраической форме 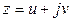на комплексной плоскости	compass(u,v) compass(z)
bar	Столбцовая диаграмма	bar(x,y) bar(x,y,w) Элементы в векторе x должны быть расположены в порядке возрастания или убывания; w – ширина столбцов диаграммы (по умолчанию 0.8); при w>1 столбцы перекрываются
pie	Круговая диаграмма	pie(x,explode) Диаграмма строится для данных, записанных в вектор x в процентном соотношении (если сумма элементов вектора больше 1, то они нормируются к своей сумме); explode – вектор из нулей и единиц, согласованный по длине с х, задающий "вытаскиваемые" сектора диаграммы
hist	Гистограмма	hist(y,x) N=hist(y,x) Гистограмма отображает число N попаданий значений элементов вектора у в интервалы, центры которых заданы элементами вектора х

Дата добавления: 2014-11-08