Функция Лапласа. Вероятность попадания в заданный интервал нормальной случайной величины. Вероятность отклонения от математического ожидания. Правило «трех сигм»

Выражение функции распределения (интегральной функции) НРСВ

F(x) =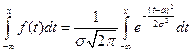

через элементарные функции невозможно. Однако для расчетов, связанных с НРСВ, необходимо знать её значения. Поэтому рассматривается функция Лапласа:

,

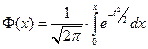для которой составлены таблицы (их можно найти в учебнике или задачнике по теории вероятностей).

При использовании таблицы следует учитывать, что функция Лапласа обладает следующими свойствами:

1) F(-х)=-F(х), т.е. является нечетной, поэтому в таблице приведены значения F(х) только при х>0.

2) при х= 4 значение функции Лапласа F(х)=0,4999, поэтому при х> 4 принято считать, что F(х)=0.5.

Функция распределения НРСВ с параметрами (а; s) выражается через функцию Лапласа следующим образом:

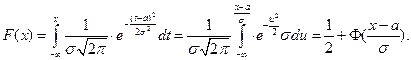
Через функцию распределения выражается вероятность попадания НРСВ Х в заданный интервал (a; b):

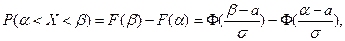
а также вероятность отклонения Х от математического ожидания а не более, чем на d:

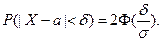
Следствием последней формулы является “правило трех сигм”,

,

которое можно сформулировать так:

НРСВ Х с параметрами (а, s) практически наверняка принимает значения только в интервале (а -3s; а +3s).

На практике “правило трех сигм” применяют также для формулировки гипотез о виде распределения:

если некоторая случайная величина удовлетворяет правилу трех сигм, то можно предположить, что она имеет распределение близкое к нормальному.

Задача. Нормально распределенная случайная величина Х задана своими параметрами – а =2 – математическое ожидание и s = 1 – среднее квадратическое отклонение. Требуется написать плотность вероятности и построить ее график, найти вероятность того, Х примет значение из интервала (1; 3), найти вероятность того, что Х отклонится (по модулю) от математического ожидания не более чем на 2.

Плотность нормального распределения имеет вид:

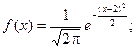
Построим график:

Найдем вероятность попадания случайной величины в интервал (1; 3).

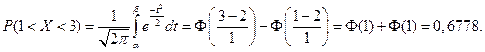
Найдем вероятность отклонение случайной величины от математического ожидания на величину, меньшую чем 2.

Дата добавления: 2014-11-16