Закон больших чисел. Неравенство Чебышева. Теорема Бернулли. Теорема Чебышева

Из повседневного опыта известно, что массовые случайные явления обладают свойствами устойчивости средних. Это означает, что при независимых испытаниях случайной величины Х среднее арифметическое (х₁+ х₂+ …+ х_n )/n полученных значений при больших n стабилизируется. Случайные колебания значений каждого испытания компенсируются и случайная величина

(х₁+ х₂+ …+ х_n,)/n,

где х_i – значение величины Х(i=1, 2,…,n) в i –м испытании при больших n теряет свой случайный характер. Теоремы описывающие такие ситуации называются законами больших чисел.

Лемма (неравенство Чебышева). Пусть Х- произвольная случайная величина, М(Х) и D(X) – её математическое ожидание и дисперсия, e >0 произвольное число. Тогда справедливо неравенство:

Р(|X-M(X)|< e)>1- D(X)/e²

где Р(|X-M(X)|< e) означает вероятность того, что отклонение случайной величины Х от её математического ожидания меньше e.

Теорема Чебышева. При достаточно большом числе независимых испытаний среднее арифметическое наблюдаемых значений случайной величины сходится по вероятности к ее –математическому ожиданию, т.е.

,

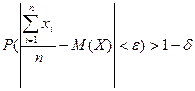где e,d - произвольные малые положительные числа.

Теорема Чебышева утверждает, что малое (меньше, чем e) отклонение среднего арифметического от математического ожидания весьма вероятно. Иными словами, почти всегда будет наблюдаться малое отклонение (при большем числе испытаний n).

Теорема Бернулли.

При неограниченном увеличении числа испытаний частота случайного события сходится по вероятности к вероятности события, т.е.

,

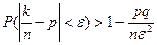если вероятность от испытания к испытанию не изменяется и равна р, то q=1-p.

Задача. Монета бросается 1000 раз. Оценить вероятность отклонения частоты появления орла от вероятности на величину меньше, чем 0,1.

Решение. Воспользуемся неравенством

,

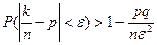Пусть n=1000 р=q=1/2, e=0,1, тогда

,

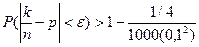Следовательно, искомая вероятность больше 39/40. Это подтверждает, что при n ® ¥ вероятность стремится к единице.

Теорему Бернулли можно рассматривать как частный случай теоремы Чебышева.

Дата добавления: 2014-11-16