
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Багатофакторний кореляційно-регресійний аналіз
|
|
|
|
У багатьох випадках на результативну ознаку впливає не один, а декілька факторів. Між ними існують складні взаємозв’язки, тому їх вплив на результативну ознаку комплексний і його не можна розглядати як просту суму ізольованих впливів.
Багатофакторний кореляційно-регресійний аналіз дозволяє оцінити ступінь впливу на досліджуваний результативний показник кожного із уведених в модель факторів при зафіксованому на середньому рівні інших факторів.
Форму зв’язку можна визначити шляхом перебору функцій різних типів, але це пов’язане зі значною кількістю зайвих розрахунків. Однак, беручи до уваги, що будь-яку функцію багатьох змінних шляхом логарифмування або заміни змінних можна звести до лінійного виду:
 .
.
Параметри рівняння знаходять за методом найменших квадратів.
Так, для розрахунку параметрів рівняння лінійної двофакторної регресії:
 ,
,
де  – розраховані значення результативної ознаки;
– розраховані значення результативної ознаки;
х 1, х 2 – факторні ознаки;
а 0, а 1, а 2 – параметри рівняння.
Система нормальних рівнянь:

Кожний коефіцієнт рівняння показує ступінь впливу відповідного фактора на результативний показник за фіксованого положення решти факторів, тобто, як зі зміною окремого фактора на одиницю змінюється результативний показник.
На основі коефіцієнтів регресії не можна робити висновок, яка із факторних ознак найбільше впливає на результативну ознаку, тому що коефіцієнти регресії між собою не порівняльні, оскільки вони володіють різними одиницями вимірювання.
З метою виявлення порівняльної сили впливу окремих факторів і резервів, які закладені в них, статистика вираховує часткові коефіцієнти еластичності  , а також бета-коефіцієнти
, а також бета-коефіцієнти  за формулами:
за формулами:
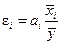 ;
;  ,
,
де аі – коефіцієнт регресії при і -му факторі;
 –середнє значення і -го фактора;
–середнє значення і -го фактора;
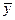 – середнє значення результативної ознаки;
– середнє значення результативної ознаки;
 – середнє квадратичне відхилення і -го фактора;
– середнє квадратичне відхилення і -го фактора;
 –середнє квадратичне відхилення результативної ознаки.
–середнє квадратичне відхилення результативної ознаки.
Часткові коефіцієнти еластичності показують, на скільки відсотків у середньому зміниться результативна ознака зі зміною на 1 % кожного фактора за фіксованого положення інших факторів.
Для визначення факторів, у розвитку яких закладені найбільші резерви покращення досліджуваної ознаки, з урахуванням ступеня варіації факторів рівняння множинної регресії, вираховують часткові 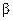 -коефіцієнти, які показують на яку частину середнього квадратичного відхилення змінюється результативна ознака зі зміною відповідної факторної ознаки на величину її середнього квадратичного відхилення.
-коефіцієнти, які показують на яку частину середнього квадратичного відхилення змінюється результативна ознака зі зміною відповідної факторної ознаки на величину її середнього квадратичного відхилення.
Для характеристики ступеня тісноти зв’язку в множинній прямолінійній кореляції використовують множинний коефіцієнт кореляції.
 ,
,
де  – множинний коефіцієнт кореляції;
– множинний коефіцієнт кореляції;
 –парні коефіцієнти лінійної регресії, які визначаються за формулами:
–парні коефіцієнти лінійної регресії, які визначаються за формулами:
 ;
; 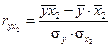 ;
;  .
.
Множинний коефіцієнт кореляції показує, яку частину загальної кореляції складають коливання, під впливом факторів х 1, х 2,..., хп,закладених у багатофакторну модель для дослідження.
Множинний коефіцієнт кореляції коливається в межах від 0 до ± 1. При R = 0 зв'язок між досліджуваними ознаками відсутній, при R = ±1 – функціональний.
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 752; Нарушение авторских прав?; Мы поможем в написании вашей работы!