Нелінійні залежності

На практиці економічного аналізу найбільш часто використовують наступні нелінійні функції залежності: гіперболічну, параболічну другого порядку, напівлогарифмічну та деякі інші.

Якщо результативна ознака зі збільшенням факторної ознаки зростає або спадає не безкінечно, а прямує до кінцевої мети, то для її аналізу застосовують рівняння гіперболи:

.

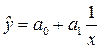Для знаходження параметрів цього рівняння методом найменших квадратів використовується система нормальних рівнянь:

.

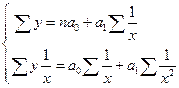За методом найменших квадратів параметри гіперболи визначають за формулами:

; .

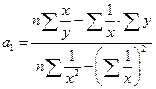Графік гіперболи має вид (рис. 8.3).

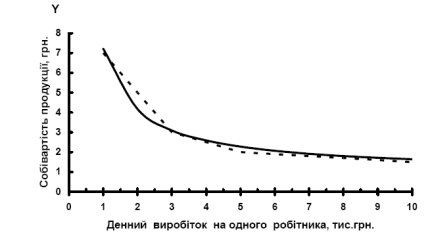
Рисунок 8.3 – Графік кореляційної залежності собівартості одиниці продукції від денного виробітку на одного робітника

Для визначення тісноти зв’язку між результативною і факторною ознаками обчислюємо кореляційне відношення за формулою:

.

Парабола другого порядку застосовується в тих випадках, коли зі зростанням факторної ознаки відбувається нерівномірне зростання або спадання результативної ознаки. Рівняння параболи другого порядку визначається за формулою:

.

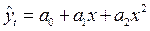Параметри цього рівняння знаходять методом найменших квадратів шляхом складання і розв’язання системи нормальних рівнянь:

.

З метою оцінки тісноти зв’язку визначають кореляційне відношення:

.

Графік параболи другого порядку має вид (рис. 8.4).

Рисунок 8.4 – Графік параболічної залежності

між факторною та результативною ознаками

Вирівнювання за напівлогарифмічною кривою проводять у тих випадках, коли зі зростанням факторної ознаки, середня результативна ознака спочатку до певних меж зростає досить швидко, але пізніше темпи її зростання поступово сповільнюються. Напівлогарифмічна функція має вид:

.

Для знаходження параметрів напівлогарифмічної функції методом найменших квадратів, розв’язують систему двох рівнянь:

Графік напівлогарифмічної кривої має вид:

Рисунок 8.5 – Графік напівлогарифмічної залежності

між факторною та результативною ознаками

Дата добавления: 2014-11-08