Виявлення тенденцій розвитку явищ

Виявлення основної тенденції (тренда) ряду, є одним із головних методів аналізу й узагальнення динамічних рядів. Зображена на графіку лінія тренда динамічного ряду покаже плавну зміну досліджуваного явища в часі, яке звільнене від короткочасних відхилень, викликаних різними причинами. В статистичній практиці виявлення основної тенденції розвитку явищ у часі проводиться методами укрупнення інтервалів, ковзної середньої та аналітичним вирівнюванням.

Одним із найпростіших способів оброблення ряду з метою виявлення закономірності зміни його рівнів є укрупнення інтервалів (періодів) часу. Сутність цього методу полягає в тому, що дані динамічного ряду об'єднуються в групи за періодами і розраховується середній показник на період – триріччя, п'ятиріччя і т.д.

Укрупнення інтервалів проілюструємо за даними наступного прикладу (табл. 10.3).

У наслідок проведених укрупнених інтервалів, отримали нові ряди динаміки, сумарного і середньорічного випуску продукції за три роки, які показують тенденцію його зростання.

Важливим способом виявлення загальної тенденції ряду динаміки є згладжування за допомогою ковзної середньої. Тут також вдаються до укрупнення періодів, але воно проводиться шляхом послідовних зміщень на одну дату при збереженні постійного інтервалу періоду.

Таблиця 10.3 – Метод укрупнення інтервалів

Роки	Випуск продукції, тис. грн.	Сумарний випуск продукції, тис. грн. (за триріччя)	Середній випуск продукції, тис. грн. (за триріччя)
	15,6
	16,0	50,5	16,8
	18,9
	15,7
	20,0	55,3	18,4
	19,6
	19,8
	21,5	61,3	20,4
	20,0
	27,3
	24,4	79,9	26,6
	28,2
	27,9
	33,1	93,7	31,2
	32,7

Порядок розрахунку ковзної середньої покажемо за даними попереднього прикладу (табл. 10.4).

Таблиця 10.4 – Розрахунок трирічної ковзної середньої

Роки	Випуск продукції, тис. грн.	Сумарний випуск продукції, тис. грн. (за триріччя)	Середній випуск продукції, тис. грн. (за триріччя)
	15,6	-	–
	16,0	50,5	16,8
	18,9	50,6	16,9
	15,7	54,6	18,2
	20,0	55,3	18,4
	19,6	59,4	19,8
	19,8	60,9	20,3
	21,5	61,3	20,4
	20,0	68,8	22,9
	27,3	71,7	23,9
	24,4	79,9	26,6
	28,2	80,5	26,8
	27,9	89,2	29,7
	33,1	93,7	31,2
	32,7	–	–

Як випливає із таблиці, вирівняний ряд, який складається з ковзних середніх показує більш плавне підвищення випуску продукції.

Найбільш ефективним способом виявлення основної тенденції є аналітичне вирівнювання.

На практиці найбільш поширеними формулами, які виражають тенденцію розвитку (тренд) явищ, є: пряма, гіпербола, парабола другого порядку, показникова функція, ряди Фур'є, логістична функція, експонента та ін.

Вирівнювання за прямою використовується в тих випадках, коли абсолютні прирости більш-менш постійні, тобто коли рівні динамічного ряду змінюються в арифметичній прогресії, або близькі до неї.

Рівняння прямої має вид:

,

де 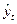– вирівняні значення динамічного ряду;

а ₀, а ₁ – параметри шуканої прямої (початковий рівень і щорічний

приріст);

t– умовне позначення часу.

Для знаходження параметрів а ₀і а ₁потрібно розв'язати за методом найменших квадратів систему нормальних рівнянь:

,

де у – фактичні рівні динамічного ряду;

п – число рівнів ряду динаміки.

При відліку часу від середини ряду, коли ∑ t = 0, тоді система рівнянь для знаходження параметрів a ₀ і a ₁ матиме вид:

звідки:

; .

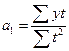Методику вирівнювання випуску продукції за рівнянням прямої покажемо на прикладі (табл. 10.5).

Таблиця 10.5 – Розрахункова таблиця для вирівнювання ряду динаміки

за прямою

Роки	Випуск продукції, тис.грн. (y)	Умовне позначення часу, (t)		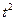	Вирівняний випуск продукції, тис. грн.. ()
	15,6	– 7		– 109,2	14,1
	16,0	– 6		– 96,0	15,3
	18,9	– 5		– 94,5	16,5
	15,7	– 4		– 62,8	17,8
	20,0	– 3		– 60,0	19,0
	19,6	– 2		– 39,2	20,2
	19,8	– 1		– 19,8	21,5
	21,5				22,7
	20,0			20,0	23,9

Таблиця 10.5 (закінчення)

	27,3			54,6	25,2
	24,4			73,2	26,4
	28,2			112,8	27,7
	27,9			139,5	28,9
	33,1			198,6	30,1
	32,7			228,9	31,4
п =15	340,7			346,1	340,7

Використовуючи розрахункові підсумки, отримуємо:

; .

Звідси рівняння прямої буде мати наступний вид: . Коефіцієнт регресії (a ₁ = 1,236) характеризує середній приріст випуску продукції за рік. Величина 22,713 буде показувати теоретичний випуск продукції 2003 р., для якого ми взяли 0 – номер року. Підставляючи у рівняння послідовно значення t (-7, -6, -5 і т.д.), отримаємо вирівняний (теоретичний) ряд динаміки випуску продукції.

Результати проведеного аналітичного вирівнювання ряду динаміки випуску продукції за 1996-2010 pp. і фактичні дані покажемо на графіку (рис. 10.2.).

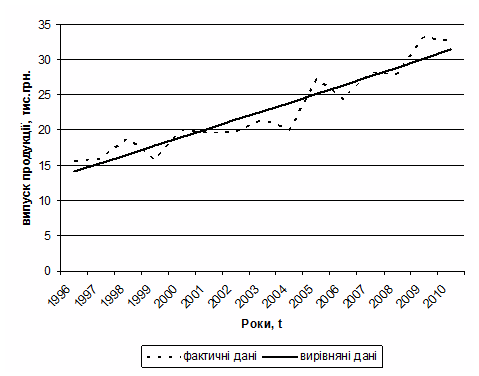
Рисунок 10.2 – Випуск продукції за 1996–2010 рр.

Вирівнювання за гіперболою проводиться тоді, коли з плином часу ряд динаміки зростає або спадає до певної межі.

Рівняння гіперболи визначається за формулою:

.

Для знаходження параметрів а₀ і а ₁у даному рівнянні методом найменших квадратів застосовують систему нормальних рівнянь:

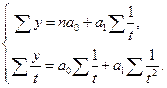
Якщо домогтися, щоб 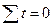, тоді параметри а₀ і а ₁знаходять за новою системою рівнянь:

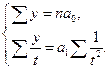
Перетворивши цю систему рівнянь у логарифмічну, будемо мати:

Звідси:

, .

При вирівнюванні за параболою другого порядку 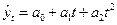параметри а ₀, а ₁, і а ₂ визначаються методом найменших квадратів, для чого складають і розв'язують систему нормальних рівнянь:

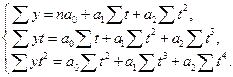
Якщо домогтися, щоб 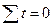, тоді і , а отже, система рівнянь спроститься:

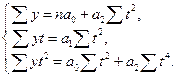
Із цієї системи 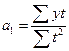, а параметри а ₀і а ₂визначаються розв'язанням системи двох рівнянь з двома невідомими.

Параметри рівняння параболи другого порядку потрібно інтерпретувати наступним чином: а ₀– це величина, яка виражає середні умови утворення рівнів ряду; а ₁– швидкість розвитку даних динамічного ряду; а ₂ – характеризує прискорення цього розвитку.

Вирівнювання за показниковою функцією проводиться в тих випадках, коли динамічний ряд розвивається в геометричній прогресії, тобто тоді, коли ланцюгові темпи зростання більш-менш постійні.

Показникова функція описується рівнянням:

.

Для визначення параметрів а₀ і а ₁цього рівняння методом найменших квадратів попередньо логарифмують рівні, тоді логарифми показникової функції описують лінійною функцією: 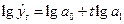. Система нормальних рівнянь має вид:

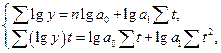
коли домогтися, що 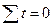, тоді

звідки ; .

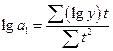Коефіцієнт а ₁, у показниковій функції характеризує середній темп зростання досліджуваної ознаки.

Вирівнювання радів динаміки використовують також для знаходження відсутніх членів ряду за допомогою інтерполяції і екстраполяції.

Інтерполяцією називається в статистиці знаходження відсутнього показника всередині ряду. Наприклад, на початок 2010 року в оператора мобільного зв’язку нараховувалось 10 тис. абонентів. Потрібно визначити ймовірну чисельність абонентів на 01.04.2010 р.

Визначимо річний абсолютний приріст абонентів:

∆_у=у_і – у ₁ = 12,4 – 10,0 = 2,4 тис. абонентів.

Знаходимо середньомісячний абсолютний приріст:

тис. абонентів.

Якщо припустити, що кожного місяця абсолютний приріст абонентів був приблизно однаковий, тоді на 01.04.2010 р. в оператора нараховувалось 10,6 тис. абонентів:

тис. абонентів.

Екстраполяцією в статистиці називається знаходження невідомих рівнів в кінці або на початку динамічного ряду. Звернемось до прикладу. Нехай в місті на 01.01.2010 р. проживало 200 тис. чол. Середньорічний темп приросту за попередні п'ять років склав 2 %. Потрібно визначити ймовірну чисельність населення міста на 01.01.2015 р.

Для знаходження перспективної чисельності населення станом на 01.01.2015 р. використовуємо формули:

, або ;

тис. чол.

або

тис. чол.

Як інтерполяція, так і екстраполяція ґрунтуються на припущенні, що наяв­ні величини цілком достатньо визначають темп розвитку досліджуваного явища і, отже, його можна розповсюджувати на відсутні рівні динамічного ряду.

Дата добавления: 2014-11-08