Студопедия

КАТЕГОРИИ:

Главная
Случайная страница
Познавательное
Новые статьи
Контакты
Заказать работу

Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)

Арифметические операции в двоичной и кратных ей системах счисления


123456789Следующая ⇒


Арифметические операции в позиционных системах счисления производится по единому алгоритму. Так, сложение двоичных чисел происходит по классическому алгоритму «столбиком» с переносом числа, кратного двум, единицей в следующий разряд.

Рассмотрим этот алгоритм на примере двух двоичных чисел 10101012 и 1101112:

Дописывание единицы                
Первое слагаемое                
Второе слагаемое                
Сумма                

Результат сложения выглядит как 100011002. Проверим результат сложения, для чего переведем все числа в десятичную систему счисления:

10101012=8510, 1101112=5510, 100011002=14010, 8510+5510=14010.

Двоичная система, являющаяся основой компьютерной арифметики, весьма громоздка и неудобна для использования человеком. Поэтому используют две кратные двоичной системы счисления: восьмеричную и шестнадцатеричную. В случае шестнадцатеричной системы арабских цифр не хватает, и в качестве цифр используются первые шесть заглавных букв латинского алфавита. Примеры записи натуральных чисел от 1 до 16 в четырех системах счисления помещены в Таблице 1.

 

Таблица 2. Примеры записи натуральных чисел от 1 до 16 в четырех системах счисления

10-чная 2-чная 8-чная 16-ичная
       
       
       
       
       
       
       
       
       
       
      А
      В
      С
      D
      E
      F
       

Из Таблицы 1 видно, что в двоичной системе запись чисел второй восьмерки (от 8 до 15) отличается от записи первой восьмерки (от 0 до 7) наличием единицы в четвертом (справа) разряде. На этом основан алгоритм перевода двоичных чисел в восьмеричные «по триадам». Для применения этого алгоритма надо разбить двоичное число на тройки цифр (считая справа) и записать вместо каждой из троек восьмеричную цифру:

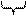
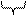
101011012 → 10 101 101 → 2558.

2 5 5

Крайняя левая тройка может быть неполной (как в примере), для получения полных троек можно приписать слева недостающие нули.

Убедимся в правильности алгоритма:

101011012 → 1*27+1*25+1*23+2*21+1*20=17310;

2558 →2*26+5*23+5*20=17310.

Для перевода чисел из восьмеричной системы в двоичную используется обратный алгоритм: восьмеричные цифры заменяются на тройки двоичных цифр (при необходимости слева дописываются недостающие нули):

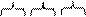3258 → 3 2 5 → 11 010 101 → 110101012.

011 010 101

Для перевода чисел из двоичной системы в шестнадцатеричную используется алгоритм «по тетрадам». Строка двоичных цифр разбивается на четверки и вместо них записываются шестнадцатеричные цифры:

101011012 → 1010 1101 → AD16.

А D

Аналогично работает и обратный алгоритм: вместо шестнадцатеричных цифр подставляются четверки двоичных цифр.

Из восьмеричной системы в шестнадцатеричную и обратно проще переводить через двоичную систему:

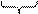D516→ D 5 →1101 0101 → 110101012 → 11 010 101 → 3258.

D 5 3 2 5

Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же правилам. Для проведения арифметических операций над числами, представленными в различных системах счисления, необходимо предварительно преобразовать их в одну систему счисления и учесть то, что перенос в следующий разряд при операции сложения и заем из старшего разряда при операции вычитания определяется величиной основания системы счисления. Лучше всего пользоваться той системой, в которой должен быть представлен результат.

Арифметические операции в двоичной системе счисления основаны на таблицах сложения, вычитания и умножения одноразрядных двоичных чисел.

При сложении двух единиц происходит переполнение разряда и производится перенос единицы в старший разряд, при вычитании 0–1 производится заем из старшего разряда, в таблице «Вычитание» этот заем обозначен 1 с чертой над цифрой.

Сложение   Вычитание   Умножение
0+0 =     0-0 =     0·0 =  
0+1 =     0-1 =     0·1 =  
1+0 =     1-0 =     1·0 =  
1+1 =     1-1 =     1·1 =  

Пример. Сложить числа:

а) 10000000100(2)+ 111000010(2)= 10111000110(2);

б) 223,2(8)+ 427,54(8) = 652,74(8);

в) 3В3,6(16)+38В,4(16)=73Е,А(16).

 

+   223,2 +   3В3,6 +
    457,54   38В,4
    652,74   73Е,А

 

Пример. Выполнить вычитание:

а) 1100000011,011(2) - 101010111,1(2) = 110101011,111(2);

б) 1510,2(8) - 1230,54(8) = 257,44(8);

в) 27D,D8(16) - 191,2(16) = ЕС,В8(16).

1100000011,011 -   1510,20 -   27D,D8 -
101010111,100   1230,54   191,20
110101011,111   257,44   ЕС,В8

 

Пример. Выполнить умножение:

а) 100111(2)·1000111(2) = 101011010001(2);

б) 1170,64(8)·46,3(8) = 57334,134(8);

в) 61,А(16)·40,D(16) = 18В7,52(16).

·   1170,64 ·   61,А ·
    46,30   40,D
    3.55234   4F52
    57334,134   18В7,52

 


Задания

Задание 1. Переведите числа в 2-ую систему счисления.

Вариант число1 число2 число3
  40010 5508 40A16
  68910 3178 6B916
  81510 5558 8A516
  71110 1748 C1116
  29010 4268 29D16
  66810 5458 6F816
  19010 7308 A9016
  20310 5778 2B316
  12010 4408 D2016
  16710 6778 16A16
  60510 5668 6C516
  25710 2568 E5716
  15710 3758 A5716
  41510 2468 4B516
  80610 4768 52816
  52810 2358 80616
  21910 1128 2D916
  92210 3148 92216
  17110 4438 DA116
  26010 3518 D6016
  11110 6238 1C116
  61410 7778 61416
  50710 2408 5B716
  16210 3338 C6216
  59110 2128 59D16
  64410 2378 6F416
  38010 1048 38E16
  11010 7438 C1A16
  32010 1028 32E16
  44910 1328 B4916

Задание 2. Переведите числа в 8-ую систему счисления.

Вариант число1 число2 число3
  11101111012 38910 A2816
  11010101102 58710 6B616
  10110110002 63610 16816
  10110000112 56010 46C16
  10011110112 44310 D6316
  10010110102 95010 1E416
  10001001112 78110 13F16
  01111110002 56810 93116
  01111011102 82210 1A416
  01110100012 26610 64616
  01110011102 18810 8B516
  01100001102 20310 23C16
  01011100102 98610 99016
  01010101002 51910 D3916
  01010000102 32710 2E916
  01001110112 23410 47F16
  00110101002 42110 A3816
  00110100102 10410 68B16
  00110011012 94810 C2916
  00101110102 37510 57D16
  00100111102 18610 33F16
  00100110012 15610 8E416
  00100011002 47210 AB716
  00100010012 55510 18C16
  00100010002 21810 5E716
  00100001002 44210 84A16
  00011110112 12910 F4716
  00011101112 13510 6D316
  00011101012 26210 85C16
  00011011102 95310 A2C16

Задание 3. Переведите числа в 10-ую систему счисления.

Вариант число1 число2 число3
  10110000112 1748 D6316
  10001001112 2468 8B516
  01110100012 5508 D3916
  01111011102 4768 68B16
  01100001102 5668 AB716
  10011110112 2378 6D316
  00011110112 4438 C2916
  01001110112 3518 47F16
  00100011002 7438 A2816
  00110011012 3148 A3816
  00011011102 5558 1E416
  01111110002 7778 85C16
  00110100102 3338 33F16
  00011101012 6778 F4716
  00100010002 5458 18C16
  00100111102 1048 16816
  01010101002 6238 A2C16
  01010000102 2568 6B616
  10010110102 3178 1A416
  01011100102 4268 84A16
  00101110102 1028 93116
  00100010012 1128 5E716
  10110110002 7308 64616
  00100001002 5778 46C16
  01110011102 1328 13F16
  00110101002 4408 23C16
  00100110012 3758 8E416
  11010101102 2358 99016
  11101111012 2128 2E916
  00011101112 2408 57D16

Задание 4. Переведите числа в 16-ую систему счисления.

Вариант число1 число2 число3
  00100000012 7778 43310
  00111100112 1358 16610
  00011111112 1408 12510
  01010111002 1148 28710
  11101011102 1178 14710
  00101011112 1658 11910
  00011110102 5368 18910
  01100100102 7178 33810
  00101011012 6568 32710
  00011101012 3148 17410
  00011010102 1068 18710
  00111101102 1208 72510
  00100111102 2768 58910
  00011101112 2218 28310
  10110011112 1508 13710
  01001111002 1468 11310
  01111100112 1618 10610
  00011001012 5748 45910
  10001001002 1568 59610
  01000001002 1028 83310
  00100100002 6368 29410
  10010001012 7238 33710
  00110110002 7228 71410
  01000000102 2028 16210
  00100011012 2178 69210
  00101010102 2748 85710
  01010001012 1058 25410
  00011011102 6218 15910
  10011011002 1758 14110
  00100001112 6678 57110

 

Задание 5. Записать результат сложения двух чисел в 2-ой системе счисления.

Вариант число1 число2
  981,1910 140,638
  688,4810 344,048
  339,4710 323,068
  909,2410 177,338
  412,8510 227,368
  506,1610 675,638
  169,7410 636,758
  480,9010 102,618
  181,0510 145,628
  112,5110 154,038
  135,6710 371,548
  937,4510 275,208
  635,0610 137,248
  125,9410 171,848
  213,5310 542,028
  198,9310 134,128
  307,4910 125,228
  572,3210 230,768
  977,6410 671,638
  446,8010 507,078
  182,0910 456,358
  372,6410 265,508
  229,2810 624,358
  266,6210 104,348
  701,6710 155,678
  487,5910 434,438
  182,4710 171,148
  116,8510 465,648
  227,5610 274,358
  669,8810 634,548

Задание 6. Записать результат сложения двух чисел в 10-ой системе счисления.

Вариант число1 число2
  0101011001002 140,9316
  0101001001112 3A8,0816
  0011100011102 39B,0616
  1001000000102 177,C316
  0110111111002 2D7,8616
  0001100001102 68E,6316
  0000000101002 F36,7916
  0001100101102 10C,6116
  0101111111112 185,D216
  0000110111012 15A,0316
  0101010111112 B71,5416
  0011010010002 279,C016
  0000110100012 1D7,2816
  0010111100112 179,E416
  0001011101112 54F,0216
  0101010000102 134,A916
  0101110010012 82B,2216
  0000001000002 230,7C16
  0111010011102 6D1,6316
  0100101110012 508,E816
  0011000011112 8F6,3516
  0011000000002 268,5D16
  0000011011002 624,9816
  0011110100102 1A4,3416
  0011110001002 155,B716
  1001010011002 4C4,4316
  0011010001112 191,1D16
  0001000000012 4E9,9416
  0000101110002 274,F516
  0000101010002 A38,5416

Задание 7. Записать разность двух чисел в 8-ой системе счисления.

Вариант число1 число2
  0011100011102 169,7410
  0011000011112 480,9010
  0101011001002 181,0510
  0000000101002 112,5110
  0111010011102 135,6710
  0100101110012 937,4510
  0101001001112 182,0910
  0000110100012 981,1910
  0010111100112 688,4810
  0001011101112 339,4710
  0101010000102 909,2410
  0101110010012 412,8510
  0000001000002 506,1610
  0011110001002 372,6410
  1001010011002 229,2810
  0001100101102 266,6210
  0101111111112 446,8010
  1001000000102 116,8510
  0011000000002 227,5610
  0000011011002 669,8810
  0011110100102 701,6710
  0000110111012 487,5910
  0101010111112 182,4710
  0011010010002 635,0610
  0110111111002 125,9410
  0001100001102 213,5310
  0000101110002 198,9310
  0000101010002 307,4910
  0011010001112 572,3210
  0001000000012 977,6410

Задание 8. Записать разность двух чисел в 16-ой системе счисления.

Вариант число1 число2
  0000011101012 434,438
  0000101010002 171,148
  0001111101102 140,638
  0010110000102 344,048
  0001111111002 323,068
  0001101001012 177,338
  0000111001012 227,368
  0011110000002 675,638
  0000100100112 636,758
  0010111010002 137,248
  0011011110112 171,848
  0000100010112 542,028
  0000111011012 134,128
  0000010011002 125,228
  0001011001112 634,548
  1000000111102 102,618
  0000100100002 145,628
  0101011100012 154,038
  0010100010112 371,548
  0001011110102 275,208
  0010100101102 230,768
  0000111110002 671,638
  0001100000002 507,078
  0010000100012 456,358
  0000001101112 265,508
  0100111001012 624,358
  1001110110012 104,348
  0010010010002 155,678
  0011111100012 465,648
  0011101100002 274,358

Задание 9. Записать результат умножения двух чисел в 2-ой системе счисления.

Вариант число1 число2
  242,9610 F36,7916
  223,8310 10C,6116
  581,0710 185,D216
  424,6110 15A,0316
  202,9210 140,9316
  113,0810 3A8,0816
  126,3510 39B,0616
  815,2510 82B,2216
  366,6110 230,7C16
  586,1110 6D1,6316
  153,4110 508,E816
  140,0710 8F6,3516
  186,7710 268,5D16
  454,1910 155,B716
  652,0710 4C4,4316
  103,3210 177,C316
  220,6310 2D7,8616
  279,0410 68E,6316
  733,6610 191,1D16
  364,5310 4E9,9416
  144,0010 274,F516
  612,3410 A38,5416
  323,5010 B71,5416
  661,5810 279,C016
  146,1110 1D7,2816
  248,0910 179,E416
  761,6310 624,9816
  178,1710 1A4,3416
  162,9710 54F,0216
  626,4410 134,A916

Задание 10. Записать результат умножения двух чисел в 10-ой системе счисления.

Вариант число1 число2
  103,328 14A,0716
  113,058 186,B716
  126,358 454,1916
  136,778 364,5316
  140,078 144,DD16
  144,558 6C2,3416
  146,118 242,9616
  153,418 223,E316
  162,778 581,0716
  173,178 761,6316
  202,728 178,F716
  220,638 652,0716
  223,338 163,3216
  242,768 4A4,6116
  243,048 202,9216
  277,048 113,B816
  315,418 323,5C16
  323,508 661,5816
  364,538 146,1116
  366,618 248,D916
  424,618 126,3516
  454,178 8E5,2516
  531,078 366,6116
  536,118 162,F716
  612,348 626,4416
  626,448 5F6,1116
  652,078 153,B116
  661,548 220,6316
  733,668 279,C416
  761,638 7A3,6616

 

Контрольные вопросы

1. Какие системы счисления называют позиционными, а какие — непозиционными? Приведите примеры.

2. Что называется основанием системы счисления?

3. Почему для вычислительной техники особенно важна система счисления по основанию 2?

4. Почему произошел переход от двоичных к шестнадцатеричным обозначениям в архитектуре ЭВМ?

5. Какие способы перевода целых десятичных чисел в двоичные и обратно Вы знаете?

6. Каковы правила выполнения арифметических операций над числами в двоичном представлении?

7. Как переводить целые числа из двоичного представления в восьмеричное и шестнадцатеричное представления и обратно?

8. Какое двоичное представление отрицательных целых чисел используется в вычислительной технике?

9. Дайте определение системы счисления. Назовите и охарактеризуйте свойства системы счисления.

10. Какие символы используются для записи чисел в двоичной системе счисления, восьмеричной, шестнадцатеричной?

123456789Следующая ⇒


Поделиться с друзьями:

Дата добавления: 2014-11-08; Просмотров: 1803; Нарушение авторских прав?; Мы поможем в написании вашей работы!

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
studopedia.su - Студопедия (2013 - 2025) год. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав! Последнее добавление




Генерация страницы за: 0.031 сек.