Законы логики и правила преобразования логических выражений

1. Закон двойного отрицания (двойное отрицание исключает отрицание):

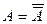
2. Переместительный (коммутативный) закон:

o для логического сложения: ;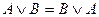

o для логического умножения: .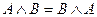

Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.

3. Сочетательный (ассоциативный) закон:

o для логического сложения: ;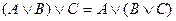

o для логического умножения: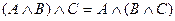

При одинаковых знаках скобки можно ставить произвольно или вообще опускать.

4. Распределительный (дистрибутивный) закон:

o для логического сложения: ;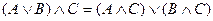

o для логического умножения: .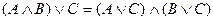

Закон определяет правило выноса общего высказывания за скобку.

5. Закон общей инверсии (законы де Моргана):

o для логического сложения: ;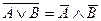

o для логического умножения: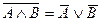

6. Закон идемпотентности (от латинских слов idem — тот же самый и potens — сильный; дословно — равносильный):

o для логического сложения: ;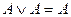

o для логического умножения: .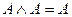

Закон означает отсутствие показателей степени.

7. Законы исключения констант:

o для логического сложения: ; ;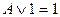

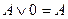o для логического умножения: ; .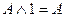

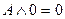8. Закон противоречия:

o .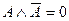

Невозможно, чтобы противоречащие высказывания были одновременно истинными.

9. Закон исключения третьего:

o .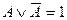

Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.

10. Закон поглощения:

o для логического сложения: ;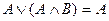

o для логического умножения: .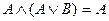

Знание законов логики позволяет проверять правильность рассуждений и доказательств. Основываясь на законах, можно выполнять упрощение сложных логических выражений. Такой процесс замены сложной логической функции более простой, но равносильной ей, называется минимизацией функции.

Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), другие - основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).

Нарушения законов логики приводят к логическим ошибкам и вытекающим из них противоречиям.

Задания

Задание 1. Составьте таблицу истинности для следующего выражения.

Вариант	Выражение	Вариант	Выражение

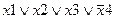
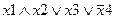
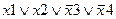
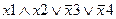
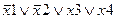
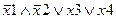
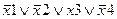
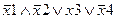
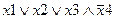
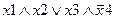
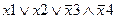
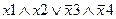
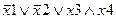
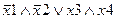
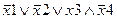
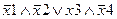
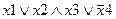
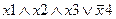
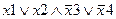
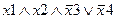
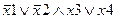
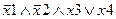
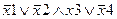
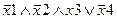
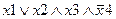
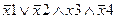
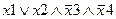
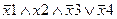
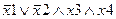
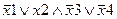
Задание 2. Раскрыть скобки и упростить выражение, составить для него таблицу истинности.

Вариант	Выражение

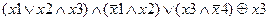
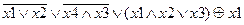
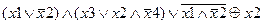
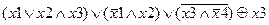
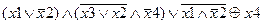
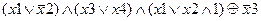
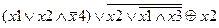
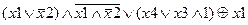
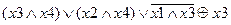
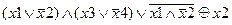
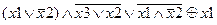
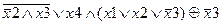
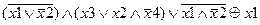
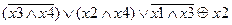
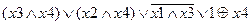
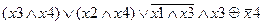
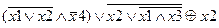
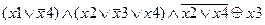
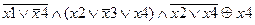
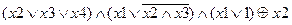
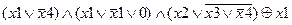
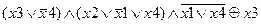
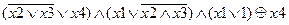
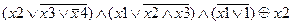
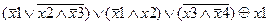
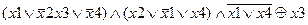
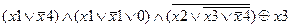
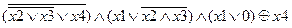
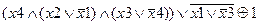
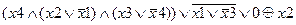
Задание 3. Минимизировать выражение с использованием карт Карно.

Вариант	Выражение

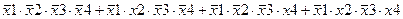
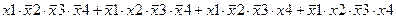
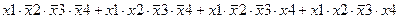
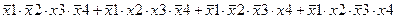
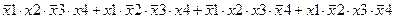
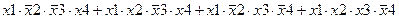
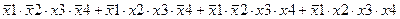
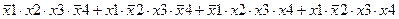
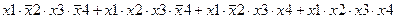
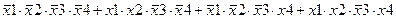
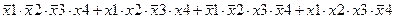
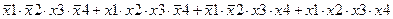
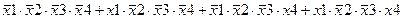
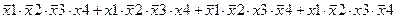
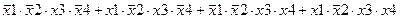
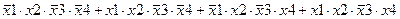
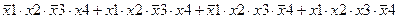
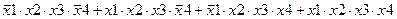
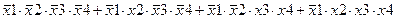
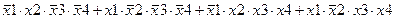
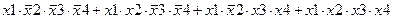
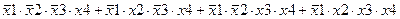
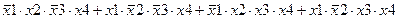
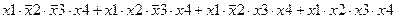
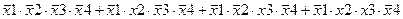
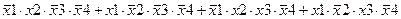
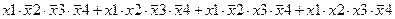
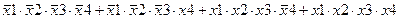
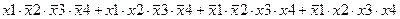
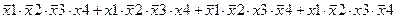
Задание 4. Минимизировать выражение и составить таблицы истинности для исходного и минимизированного выражений.

Вариант	Выражение

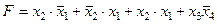
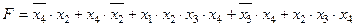
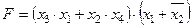
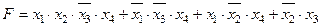
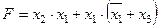
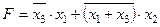
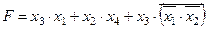
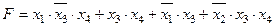
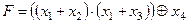
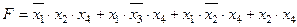
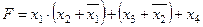
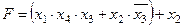
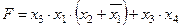
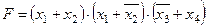
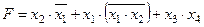
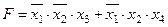
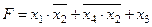
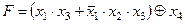
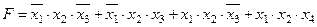
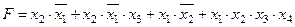
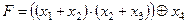
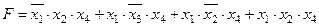
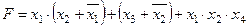
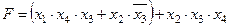
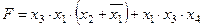
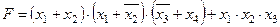
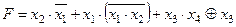
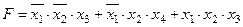
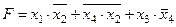
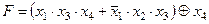
Контрольные вопросы

1. Назовите основные логические операции и приведите их таблицы истинности.

2. Что такое логическое выражение?

3. Каков порядок выполнения операций при вычислении значения логического выражения?

4. Приведите примеры логических выражений и вычисления их значений.

5. Назовите элементарные логические элементы и приведите их обозначения на схемах.

6. Изобразите электрические схемы, реализующие элементарные логические элементы.

7. Приведите примеры построения схем на логических элементах на основе логического выражения.

8. Приведите примеры построения логических выражений по заданным логическим схемам.

9. Что такое триггер? Перечислите виды триггеров и коротко их охарактеризуйте.

10. Чем отличается синхронный триггер от несинхронного?

11. Проиллюстрируйте на примерах хранение информации в триггере и запись нуля или единицы.

12. Какое состояние триггера называют недопустимым?

13. Расскажите об элементе «Исключающее ИЛИ», приведите таблицу истинности для соответствующей логической операции.

14. Расскажите о полусумматоре.

15. Расскажите о сумматоре и организации переноса «запасного» разряда.

Дата добавления: 2014-11-08