Минимизация полностью определенных булевых функций

Минимизация булевых функций

Существуют несколько способов минимизации булевых функций. Прежде всего, это аналитический символьный и аналитический кодовый методы, метод Квайна–Мак-Класки, метод Блека–Порецкого, метод обобщенных кодов и графическая минимизация с помощью карт Карно.

Пример для демонстрации аналитических методов:

.

z=01+10+11=(01+11)+(10+11)=-1+1-= x + y.

Первые четыре метода чрезвычайно громоздки и малоэффективны уже при количестве аргументов более четырёх. Метод обобщенных кодов ориентирован на использование ЭВМ, однако может использоваться и при ручном синтезе для функций от большого числа переменных.

Наиболее эффективна минимизация булевых функций с помощью карт Карно. До сих пор существует ошибочное мнение, что этим методом можно решать задачи для функций не более, чем 6 аргументов. На самом деле карты Карно могут применяться для функций даже от 8-12 переменных. На рисунке 2 представлены карты Карно для 2-6 переменных и примеры минимизации с их помощью логических функций.

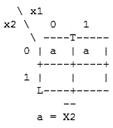
а) б) в)

г) д)

Рисунок 2 – Карты Карно для 2-6 переменных

Метод Карно основан на законе склеивания. Склеиваются наборы, отличающиеся друг от друга лишь значением одного разряда.

Такие наборы называются соседними, и они соответствуют соседним клеткам карты Карно. Формируются такие наборы (коды Грея) по принципу симметрии.

Введем определение прямоугольника Карно, под которым будем понимать некоторую, зачастую разрозненную, фигуру покрытия, удовлетворяющую принципу симметрии, т.е. сплошь состоящую из элементарных прямоугольников Карно, закодированных только соседними наборами.

Заполняются карты Карно следующим образом. Допустим, есть некая функция из четырех переменных. Карта Карно будет содержать 16 клеток (2⁴=16). Функция вот такая:

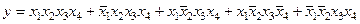
Не такая уж сложная функция. Путем преобразований можно ее немного упростить, но это потребует больших выкладок. Составим карту Карно:

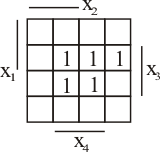
Как это все делается? Посмотрите, вторая сверху слева ячейка, в ней стоит 1 и этой единице соответствует первое слагаемое в формуле. Единица стоит именно там, поскольку в этой ячейке перекрываются все переменные. Стоит уйти на ячейку влево, вправо, вверх, вниз и одна из переменных уже перекрывать ее не будет. Если одна из переменных с инверсией, что характерно для второго слагаемого, единица ставится с учетом не перекрытия ячейки этой переменной, т. е. для второго слагаемого x₁ с инверсией и единица стоит в третьей (сверху) строке третьего столбца. Для четвертого слагаемого с инверсией переменные x₂ и x₄. Поэтому единица стоит в последней строке (второй столбец). Так проставляются все единицы. В пустых ячейках по идее стоят нули (не показаны для наглядности). Подытожим, если переменная без инверсии, ей соответствует 1, если с инверсией - 0.

После проставления всех единиц начинается объединение ячеек, в которых стоят эти самые единицы. Объединяются клетки по следующим правилам: число объединяемых клеток 2, 4, 8, 16, 32 и т. д., т. е. 2ⁿ, объединять надо как можно больше клеток, а самих объединений должно быть как можно меньше. На рисунке ниже показано, как это делается:

Если единицы стоят буквой "Т", "Г" и пр., то они также не объединяются. После объединения ячеек составляется уравнение функции. Объединенные клетки условно считаются за одну, т.е. говоря простым языком, начинается обратный процесс составления карты Карно. Судя по рисунку, четырем объединенным единицам соответствует выражение x₃x₄. То есть, область объединения попадает в зону видимости всех переменных. Во втором объединении не участвует x₂, поэтому эта переменная будет с инверсией. Таким образом, после преобразования с помощью карты Карно была получена вот такая функция:

Алгоритм "НИИРТА" графической минимизации логических функций

1.Заполнить карту Карно нулями и единицами в соответствии с таблицей истинности.

2.Покрыть все единичные наборы минимальным количеством прямоугольников Карно, каждый из которых имеет максимальную площадь.

3.Каждому прямоугольнику Карно соответствует одна импликанта, причем, если в границах прямоугольника Карно какая-либо переменная принимает значение как 0, так и 1, то она склеивается.

На рисунке 3 представлены фигуры покрытия, не являющиеся прямоугольника Карно

Рисунок 3 – Фигуры покрытия, не являющиеся прямоугольниками Карно

Дата добавления: 2014-11-08