Для отрицательных чисел

Теоретический материал

Лабораторная работа №4

Тема: «Машинные коды»

Цель работы: освоить принципы формирования машинных кодов в компьютере.

Задачи:

1) освоить принципы записи целых чисел в прямом, обратном и дополнительном кодах;

2) освоить принципы записи действительных чисел в виде кодов с плавающей точкой;

3) освоить принципы осуществления арифметических операций с действительными числами.

Для представления информации в памяти ЭВМ (как числовой, так и нечисловой) используется двоичный способ кодирования.

Элементарная ячейка памяти ЭВМ имеет длину 8 бит (байт). Каждый байт имеет свой номер (его называют адресом). Наибольшую последовательность бит, которую ЭВМ может обрабатывать как единое целое, называют машинным словом. Длина машинного слова зависит от разрядности процессора и может быть равной 16, 32 битам и т.д.

Представление числа в привычной форме «знак-величина», когда первый бит n-разрядного слова знаковый, а остальные n-1 битов представляют цифровые разряды числа в двоичной системе счисления, называется прямым кодом двоичного числа.

Прямой код целого числа полностью совпадает с записью самого числа в разрядной сетке компьютера. Прямой код отрицательного целого числа отличается от прямого кода соответствующего положительного числа содержимым знакового (старшего) разряда:

0 – для положительного числа;

Диапазон значений величин зависит от количества бит памяти, отведенных для их хранения (разрядности сетки).

Пример. Прямой код чисел Х=11011₂ и Y=-11011₂ в восьмиразрядной сетке имеет вид:

[X_пк]= 0 0011011

[Y_пк]= 1 0011011

В системе прямых кодов существует два различных представления ноля:

0 0000000 – положительный 0;

1 0000000 – отрицательный 0.

Оба представления совершенно равноправны.

Прямой код используется для хранения положительных и отрицательных чисел в запоминающих устройствах и для представления положительных чисел при выполнении операций в арифметических устройствах.

Для упрощения конструкций арифметических устройств вычислительных машин все арифметические операции, как правило, сводятся к сложению (операция вычитания) или к сериям сложений и сдвигов (операции умножения и деления).

Замена операции вычитания (алгебраического сложения) на арифметическое сложение в компьютере осуществляется с помощью обратного и дополнительного кодов.

Дополнительный код положительного числа совпадает с этим числом. Обратный код положительного числа также совпадает с этим числом.

Обратный код отрицательного числа представляет собой инверсный код прямого кода модуля этого числа. Дополнительный код целого отрицательного числа может быть получен по следующему алгоритму:

1) записать прямой код модуля числа;

2) инвертировать его (заменить единицы нулями, нули — единицами); данное представление называют обратным кодом;

3) прибавить к инверсному (обратному) коду единицу.

При получении числа по его дополнительному коду, прежде всего, необходимо определить его знак. Если число окажется положительным, то просто перевести его код в десятичную систему счисления. В случае отрицательного числа необходимо выполнить следующий алгоритм:

1) вычесть из кода числа 1;

2) инвертировать код;

3) перевести в десятичную систему счисления. Полученное число записать со знаком минус.

Пример: записать число -37₁₀ в прямом Mпк, обратном Мок и дополнительном кодах Мдк в восьмиразрядной сетке.

Мпк = 1 0100101₂;

Мок = 1 1011010₂;

Мдк = 1 1011011₂.

В некоторых случаях при представлении в памяти ЭВМ чисел используется смешанная двоично-десятичная «система счисления», где для хранения каждого десятичного знака нужен полубайт (4 бита) и десятичные цифры от 0 до 9 представляются соответствующими двоичными числами от 0000 до 1001. Например, упакованный десятичный формат, предназначенный для хранения целых чисел с 18 значащими цифрами и занимающий в памяти 10 байт (старший из которых знаковый), использует именно этот вариант.

Несколько иной способ применяется для представления в памяти персонального компьютера действительных чисел. Рассмотрим представление величин с плавающей точкой.

Любое действительное число можно записать в стандартном виде М· 10 ^р, где 1£ М< 10, р — целое. Например, 120100000 = 1,201·10⁸. Поскольку каждая позиция десятичного числа отличается от соседней на степень числа 10, умножение на 10 эквивалентно сдвигу десятичной запятой на одну позицию вправо. Аналогично деление на 10 сдвигает десятичную запятую на позицию влево. Поэтому приведенный выше пример можно продолжить: 120100000 = 1,201·10⁸= 0,1201·10⁹= 12,01·10⁷... Десятичная запятая «плавает» в числе и больше не помечает абсолютное место между целой и дробной частями.

В приведенной выше записи М называют мантиссой числа, а р – его порядком. Для того чтобы сохранить максимальную точность, вычислительные машины почти всегда хранят мантиссу в нормализованном виде. Основание системы счисления здесь, как уже отмечалось выше, – число 2. Способ хранения мантиссы с плавающей точкой подразумевает, что двоичная запятая находится на фиксированном месте. Фактически подразумевается, что двоичная запятая следует после первой двоичной цифры. Место, отводимое для числа с плавающей точкой, делится на два поля. Одно поле содержит знак и значение мантиссы, а другое содержит знак и значение порядка.

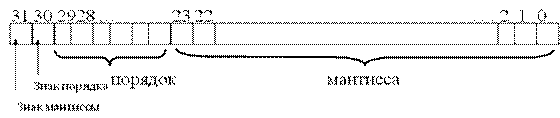
В современных компьютерах машинная форма числа хранит не сам порядок, а его смещенное значение – характеристику числа. Это сделано для того, чтобы не хранить знак порядка и, значит,

§ облегчить действия над порядками;

§ увеличить диапазон представляемых чисел.

Смещение выбирается так, чтобы минимальному значению порядка соответствовал нуль. Например, для типа Double порядок занимает 11 бит и имеет диапазон от 2^-1023 до 2¹⁰²³, поэтому смещение равно 1023₍₁₀₎=1111111111₍₂₎

Таким образом, алгоритм для получения представления действительного числа в памяти ЭВМ следующий:

1) перевести модуль данного числа в двоичную систему счисления;

2) нормализовать двоичное число, т.е. записать в виде М· 2 ^Р, где М – мантисса (ее целая часть равна 1₍₂₎) и р – порядок, записанный в десятичной системе счисления;

3) прибавить к порядку смещение и перевести смещенный порядок в двоичную систему счисления;

4) учитывая знак заданного числа (0 – положительное; 1 – отрицательное), выписать его представление в памяти ЭВМ.

Пример. Запишем код числа –312,3125.

1) Двоичная запись модуля этого числа имеет вид 100111000,0101.

2) Имеем 100111000,0101 = 1,001110000101·2⁸.

3) Получаем смещенный порядок 8+1023=1031. Далее имеем 1031₍₁₀₎=10000000111₍₂₎.

4) Окончательно

Очевидно, что более компактно полученный код стоит записать следующим образом: С073850000000000₍₁₆₎.

Другой пример иллюстрирует обратный переход от кода действительного числа к самому числу.

Пример. Пусть дан код 3FEC600000000000₍₁₆₎ или

1) Прежде всего, замечаем, что это код положительного числа, поскольку в разряде с номером 63 записан нуль. Получим порядок этого числа: 01111111110₍₂₎ = 1022₍₁₀₎; 1022 – 1023 = – 1.

2) Число имеет вид 1,1100011·2^–1 или 0,11100011.

3) Переводом в десятичную систему счисления получаем 0,88671875.

Дата добавления: 2014-11-08