Основные формулы. Кинематическое уравнение движения материальной точки (центра масс твёрдого тела) вдоль оси х

МЕХАНИКА

Кинематическое уравнение движения материальной точки (центра масс твёрдого тела) вдоль оси х

х = f(t),

где f(t) – некоторая функция времени.

Проекция средней скорости на ось х

<v_x > = ∆x ∕ ∆t.

Средняя путевая скорость

<v> = ∆s ∕ ∆t,

где ∆ s – путь, пройденный точкой за интервал времени ∆ t. Путь ∆ s в отличие от разности координат ∆х = х₂ - х₁ не может убывать и принимать отрицательные значения, т. е. ∆ѕ≥0.

Проекция мгновенной скорости на ось х

v_x = dx ∕ dt.

Проекция среднего ускорения на ось х

< a _x > = Δv_x ∕ ∆t.

Проекция мгновенного ускорения на ось х

а _x = dv_x ∕ dt.

Кинематическое уравнение движения материальной точки по окружности

φ ═ ƒ(t)¸ r = R = const.

Модуль угловой скорости

ω = dφ ∕ d t.

Модуль углового ускорения

ε = dω ∕ d t.

Связь между модулями линейных и угловых величин, характеризующих движение точки по окружности:

v = ωR, а _t = εR, а _n = ω²R,

где v – модуль линейной скорости; а _t и а _n– модули тангенциального и нормального ускорений; ω – модуль угловой скорости; ε – модуль углового ускорения; R – радиус окружности.

Модуль полного ускорения

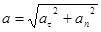, или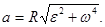

Угол между полным а инормальным а _nускорениями α =arc cos(a_n / a).

Кинематическое уравнение гармонических колебаний материальной точки

х = А cos(ω t + φ),

где х – смещение; А – амплитуда колебаний; ω – угловая или циклическая частота; φ – начальная фаза.

Скорость и ускорение материальной точки, совершающей гармонические колебания:

v = - А ω sin(ω t + φ); a = - A ω² cos(ω t + φ).

Сложение гармонических колебаний одного направления и одинаковой частоты:

а) амплитуда результирующего колебания

;

б) начальная фаза результирующего колебания

.

Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях,

x= A₁ cos ω t; y = A₂ cos(ω t + φ):

а) у = х ×А₂ / А₁, если разность фаз φ = 0;

б) у = - х ×А₂/А₁, если разность фаз φ = ±π;

в) у = х²∕ A₁ ² + y ²∕ Α₂ ² =1, если разность фаз φ = ±π/2;

Импульс p материальной точки массой m, движущейся со скоростью v,

p = m v.

Второй закон Ньютона

d p = F d t,

где F – результирующая сила, действующая на материальную точку.

Силы, рассматриваемые в механике:

а) сила упругости

F = − kx,

где k – коэффициент упругости (в случае пружины – жесткость); х – абсолютная деформация;

б) сила тяжести

P = m g;

в) сила гравитационного взаимодействия

F = G m₁ m₂ ∕ r²,

где G – гравитационная постоянная; m ₁и m ₂ – массы взаимодействующих тел; r – расстояние между телами (тела рассматриваются как материальные точки). В случае гравитационного взаимодействия силу можно выразить также через напряжённость G гравитационного поля:

F = m G;

г) сила трения (скольжения)

F = fN,

где f – коэффициент трения; N – сила нормального давления.

Закон сохранения импульса

или для двух тел (i=2)

m ₁ v ₁+ m ₂ v ₂ = m ₁ u ₁ + m ₂ u ₂,

где v ₁ и v ₂ – скорости тел в момент времени, принятый за начальный; u ₁ и u ₂ – скорости тех же тел в момент времени, принятый за конечный.

Кинетическая энергия тела, движущегося поступательно,

T = mυ² ∕ 2, или T = p² ∕ (2 m).

Потенциальная энергия:

а) упругодеформированной пружины

П = ½kx²,

где k – жёсткость пружины; x – абсолютная деформация;

б) гравитационного взаимодействия

П = - Gm₁ m₂ ∕ r,

где G – гравитационная постоянная; m₁ и m₂ – массы взаимодействующих тел; r – расстояние между ними (тела рассматриваются как материальные точки);

в) тела, находящегося в однородном поле силы тяжести,

П = mgh,

где g – ускорение свободного падения; h – высота тела над уровнем, принятым за нулевой (формула справедлива при условии h << R, где R – радиус Земли).

Закон сохранения механической энергии

E = T + П = const.

Работа A, совершаемая результирующей силой, определяется как мера изменения кинетической энергии материальной точки:

А = ∆ Т = Т₂ – Т₁.

Основное уравнение динамики вращательного движения относительно неподвижной оси z

М_z = J_z ε,

где М_z – результирующий момент внешних сил относительно оси z, действующих на тело; ε – угловое ускорение; J_z – момент инерции относительно оси вращения.

Моменты инерции некоторых тел массой m относительно оси z, проходящей через центр масс:

а) стержня длиной l относительно оси, перпендикулярной стержню,

J_z = 1/12 ml² ;

б) обруча (тонкого цилиндра) относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра),

J_z = mR ²,

где R – радиус обруча (цилиндра);

в) диска радиусом R относительно оси, перпендикулярной плоскости диска,

J_z = ½ mR ².

Проекция на ось z момента импульса тела, вращающегося относительно неподвижной оси z,

L_z = J_z ω,

где ω – угловая скорость тела.

Закон сохранения момента импульса системы тел, вращающихся вокруг неподвижной оси z,

J_z ω = const,

где J_z – момент инерции системы тел относительно оси z; ω – угловая скорость вращения тел системы вокруг оси z.

Кинетическая энергия тела, вращающегося вокруг неподвижной оси z,

Т = ½ J_z ω², или Т = L_z² ∕ (2 J_z).

Дата добавления: 2014-11-16