Основные формулы

МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА.

Количество вещества тела (системы) ,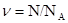

где N – число структурных элементов (молекул, атомов, ионов и т. п.), составляющих тело (систему); 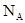- постоянная Авогадро ().

Молярная масса вещества ,

где m – масса однородного тела (системы); - количество вещества этого тела.

Относительная молекулярная масса вещества

,

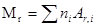где 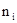- число атомов i -го химического элемента, входящих в состав молекулы данного вещества; 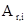- относительная атомная масса этого элемента. Относительные атомные массы приводятся в таблице Д. И. Менделеева. См. также табл. 9 Приложения.

Связь молярной массы М с относительной молекулярной массой вещества

,

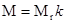где кг/моль. Количество вещества смеси газов

,

или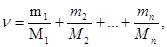

где - соответственно количество вещества, число молекул, масса, молярная масса i -го компонента смеси.

Уравнение Менделеева – Клапейрона (уравнение состояния идеального газа)

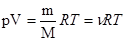
где m – масса газа, М – молярная масса газа, R – молярная газовая постоянная,

- количество вещества, Т – термодинамическая температура.

Опытные газовые законы, являющиеся частными случаями Менделеева – Клапейрона для изопроцессов:

а) закон Бойля – Мариотта (изотермический процесс: Т = const, m=c onst) = const,

или для двух состояний газа ;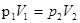

б) закон Гей – Люссака (изобарный процесс: p = const, m = const)

= const,

или для двух состояний ;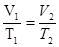

в) закон Шарля (изохорный процесс: V = const, m = const)

= const,

или для двух состояний ;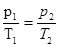

г) объединенный газовый закон (m = const)

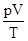=const, или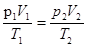

где - давление, объем, и температура газа в начальном состоянии; 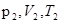- те же величины в конечном состоянии.

Закон Дальтона, определяющий давление смеси газов,

,

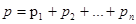где - парциальные давления компонентов смеси; n – число компонентов смеси.

Парциальным давлением называется давление газа, которое производил бы этот газ, если бы только он один находился в сосуде, занятом смесью.

Молярная масса смеси газов ,

где 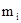- масса i -го компонента смеси; 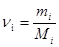- количество вещества i -го компонента смеси; n – число компонентов смеси.

Массовая доля i -го компонента смеси газа (в долях единицы или процентах)

где m – масса смеси.

Концентрация молекул

где N – число молекул, содержащихся в данной системе; - плотность вещества; V – объем системы. Формула справедлива не только для газов, но и для любого агрегатного состояния вещества.

Основное уравнение кинетической теории газов ,

где - средняя кинетическая энергия поступательного движения молекулы.

Средняя кинетическая энергия поступательного движения молекулы

,

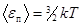где - постоянная Больцмана.

Средняя полная кинетическая энергия молекулы ,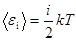

где i – число степеней свободы молекулы.

Зависимость давления газа от концентрации молекул и температуры

.

Скорости молекул:

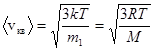- средняя квадратичная;

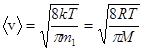- средняя арифметическая;

- наиболее вероятная,

где 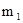- масса одной молекулы.

Относительная скорость молекулы ,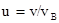

где v - скорость данной молекулы.

Средняя длина свободного пробега молекулы ,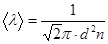

где d -эффективный диаметр молекулы.

Среднее число столкновений молекулы в единицу времени

.

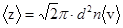Уравнение диффузии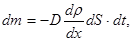

где D - коэффициент диффузии, r - плотность, dr/dx - градиент плотности,

dS - элементарная площадка, перпендикулярная оси Оx, dt - время.

Уравнение теплопроводности

где k - коэффициент теплопроводности, dT/dx - градиент температуры, dt - время.

Сила внутреннего трения ,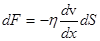

где h - коэффициент динамической вязкости, dv/dx - градиент скорости, dS - элемент площади.

Коэффициент диффузии .

Коэффициент динамической вязкости .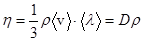

Коэффициент теплопроводности ,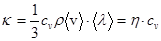

где c_V - удельная теплоемкость при постоянном объеме.

Удельные теплоемкости газа при постоянном объеме и постоянном давлении , .

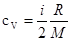Связь между удельной с и молярной С теплоемкостями

.

Дата добавления: 2014-11-16