Контрольная работа 3

Вариант	Номера задач

301. Расстояние l между свободными зарядами Q₁=180 нКл и О₂=720 нКл равно 60 см. Определить точку на прямой, проходящей через заряды, в которой нужно поместить третий заряд Q₃, так, чтобы система зарядов находилась в равновесии. Определить величину и знак заряда. Устойчивое или неустойчивое будет равновесие?

302. Два положительных точечных заряда Q и 4Q закреплены на расстоянии l =60 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд Q₁ так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещения заряда возможны только вдоль прямой, проходящей через закрепленные заряды.

303. Три одинаковых заряда Q = 1 нКл каждый расположены по вершинам равностороннего треугольника. Какой отрицательный заряд Q₁ нужно поместить в центре треугольника, чтобы его притяжение уравновесило силы взаимного отталкивания зарядов? Будет ли это равновесие устойчивым?

304. В вершинах квадрата находятся одинаковые заряды Q = -0,3 нКл каждый. Какой отрицательный заряд Q₁ нужно поместить в центре квадрата, чтобы сила взаимного отталкивания положительных зарядов была уравновешена силой притяжения отрицательного заряда?

305. Расстояние между двумя точечными зарядами Q₁=l мкКл и Q ₂=- Q₁ равно 10 см. Определить силу F, действующую на точечный заряд Q=0,1 мкКл, удаленный на r₁=6 см от первого и на r₁=8 см от второго зарядов.

306. В вершинах правильного шестиугольника со стороной а =10 см расположены точечные заряды Q, 2Q, 3Q, 4Q, 5Q, 6Q (Q = -0,1 мкКл). Найти силу F, действующую на точечный заряд Q, лежащий в плоскости шестиугольника и равноудаленный от его вершин.

307. Два одинаковых проводящих заряженных шара находятся на расстоянии r=60 см. Сила отталкивания F₁ шаров равна 70 мкН. После того как шары привели в соприкосновение и удалили друг от друга на прежнее расстояние, сила отталкивания возросла и стала равной F₂ =160 мкН. Вычислить заряды Q₁ и Q₂, которые были на шарах до их соприкосновения. Диаметр шаров считать много меньшим расстояния между ними.

308. Точечные заряды Q₁=20 мкКл, Q₂ = -10 мкКл находятся на расстоянии d =5 см друг от друга. Определить напряженность поля в точке, удаленной на r ₁=3 см от первого и на r ₂=4 см от второго заряда. Определить также силу 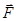, действующую в этой точке на точечный заряд Q=l мкКл.

309. Три одинаковых точечных заряда Q₁=Q₂ = Q₃=2 нКл находятся в вершинах равностороннего треугольника со сторонами a =10 см. Определить модуль и направление силы 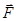, действующей на один из зарядов со стороны двух других.

310. Два положительных точечных заряда Q и 4Q закреплены на расстоянии d =10 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещения зарядов возможны только вдоль прямой, проходящей через закрепленные заряды.

311. Тонкий стержень длиной l =20 см несет равномерно распределенный заряд t=0,1 мкКл. Определить напряженность 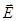электрического поля, создаваемого распределенным зарядом в точке A, лежащей на оси стержня на расстоянии а =20 см от его конца.

312. По тонкому полукольцу радиуса R =10 см равномерно распределен заряд с линейной плотностью t=1 мкКл/м. Определить напряженность 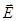электрическо­го поля, создаваемого распределенным зарядом в точке O, совпадающей с центром кольца.

313. Бесконечный тонкий стержень, ограниченный с одной стороны, несет равномерно распределенный заряд с линейной плотностью

t=0,5 мкКл/м. Определить напряженность 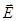электрического поля, создаваемого рас­пределенным зарядом в точке A, лежащей на оси стержня на расстоянии а =20 см от его начала.

314. По тонкому кольцу радиусом R =20 см равно­мерно распределен с линейной плотностью t=0,2 мкКл/м заряд. Определить напряженность 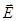электрического поля, создаваемого распределенным зарядом в точке A, находящейся на оси кольца на расстоянии h=2R от его центра.

315. Две трети тонкого кольца радиусом R =10 см несут равномерно распределенный с линейной плотностью t=0,2 мкКл/м заряд. Определить напряженность 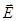элек­трического поля, создаваемого распределенным зарядом в точке O, совпадающей с центром кольца.

316. Тонкое кольцо несет распределенный заряд Q=0,2 мкКл. Определить напряженность 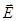электрического поля, создаваемого распределенным зарядом в точке A, равноудаленной от всех точек кольца на расстояние r = 20см. Радиус кольца R =10 см.

317. Четверть тонкого кольца радиусом R= 10 см несет равномерно распределенный заряд Q=0,05 мкКл. Определить напряженность 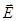электрического поля, создаваемого распределенным зарядом в точке O, совпадающей с центром кольца.

318. По тонкому кольцу равномерно распределен заряд Q=10 нКл с линейной плотностью t=0,01 мкКл/м. Определить напряженность 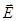электрического поля, создаваемого распределенным зарядом в точке A, лежащей на оси кольца и удаленной от его центра на расстояние, равное радиусу кольца.

319. Треть тонкого кольца радиуса R =10 см несет распределенный заряд Q=50 нКл. Определить напряженность 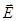электрического поля, создаваемого распределенным зарядом в точке O, совпадающей с центром кольца.

320. По тонкому полукольцу равномерно распределен заряд Q=20 мкКл с линейной плотностью t=0,1 мкКл/м. Определить напряженность 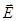электрического поля, создаваемого распределенным зарядом в точке O, совпа­дающей с центром кольца.

321. 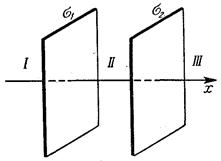На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями s₁ и s₂. Требуется: 1) используя теорему Остроградского-Гаусса и принцип суперпози­ции электрических полей, найти выражение Е(х) напря­женности электрического поля в областях: I, II и III. Принять s₁=2s, s₂=s; 2) вычислить напряженность Е поля в точке, расположенной слева от плоскостей, и ука­зать направление вектора 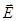; 3) построить график Е(х).

322. Условие задачи 321. В п. 1 принять s₁=-4s, s₂=2s. В п. 2 принять s=40 нКл/м² и точку расположить между плоскостями.

323. Условие задачи 321. В п. 1 принять s₁=s, s₂=-2s. В п. 2 принять s=20 нКл/м² и точку располо­жить справа от плоскостей.

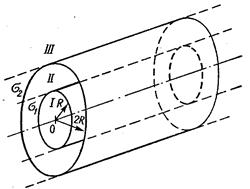324. На двух коак­сиальных бесконечныхцилиндрах радиусами R и 2 R равномерно распре­делены заряды с поверх­ностными плотностями s₁ и s_2. Требуется: 1) используя теорему Остроградского-Гаусса: найти зависимость Е (r)напряженности электри­ческого поля от расстоя­ния для трех областей: I, II и III. Принять s₁=-2s, s₂=s; 2) вычислить напря­женность Е в точке, удаленной от оси цилиндров на рас­стояние r, и указать направление вектора 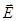. Принять s = 50 нКл/м², r =1,5 R; 3) построить график E(r).

325. См. условие задачи 324. В п. 1 принять s₁=s, s₂=-s. В п. 2 принять s=60 нКл/м², r =3 R.

326. См. условие задачи 324. В п. 1 принять s₁=-s, s₂=4s. В п. 2 принять s=30 нКл/м², r =4 R.

327. На двух концентрических сферах радиусом R и 2 R равномерно распределены заряды с поверхностными плотностями s₁ и s₂. Требуется:

1) используя теорему Остроградского-Гаусса, найти зависимость E (r)напряженности электрического поля от расстояния для трех областей: I, II и III. Принять s₁=4s, s₂ = s; 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора 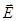. Принять s = 30 нКл/м², r =1,5 R; 3) построить график E _{( r )}.

328. Условие задачи 327. В п. 1 принять s₁=s, s₂=-s. В п. 2 принять s=0,1 мкКл/м², r =3 R.

329. Условие задачи 327. В п. 1 принять s₁=-4s, s₂=s. В п. 2 принять s=50 нКл/м², r =1,5 R.

330. Условие задачи 327. В п. 1 принять s₁=-2s, s₂=s. В п. 2 принять s = 0,1 мкКл/м², r =3 R.

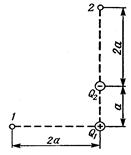
331. Электрическое поле создано зарядами Q₁=2 мкКл и Q₂=-2 мкКл, находящимися на расстоянии а= 10 см друг от друга. Определить работу сил поля, совершаемую при перемещении заряда Q=0,5 мкКл из точки 1 в точку 2.

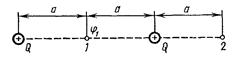
332. Электрическое поле создано двумя одинаковыми положительными точечными зарядами Q. Найти работу А _1,2 сил поля по перемещению заряда Q₁=10 нКл из точки 1 с потенциалом φ₁=300 В в точ­ку 2.

333. Тонкий стержень согнут в кольцо радиусом R= 1 0 см. Он заряжен с линейной плотностью τ=300 нКл/м. Какую работу A надо совершить, чтобы перенести за­ряд Q=5 нКл из центра кольца в точку, расположенную на оси кольца на расстоянии равном радиусу от центра его?

334. Тонкий стержень согнут в кольцо радиусом R =10 см. Он равномерно заряжен с линейной плотностью заряда t=800 нКл/м. Определить потенциал j в точке, расположенной на оси кольца на расстоянии h =10 см от его центра.

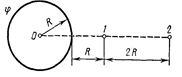
335. Электрическое поле создано заряженным прово­дящим шаром, потенциал j которого 300 В. Определить работу сил поля по перемещению заряда Q =0,2 мкКл из точки 1 в точку 2.

336. Две параллельные заряженные плоскости, по­верхностные плотности заряда которых s₁=2 мкКл/м² и s₂=-0,8 мкКл/м², находятся на расстоянии d =0,6 см друг от друга. Определить разность потенциа­лов U между плоскостями.

337. Электрическое поле образовано бесконечно длин­ной заряженной нитью, линейная плотность заряда кото­рой t= 20 пКл/м. Определить разность потенциалов U двух точек поля, отстоящих от нити на расстоянии r ₁=8 см и r ₂=12 см.

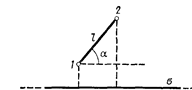338. Электрическое поле создано бесконечной равномерно за­ряженной плоскостью с поверхностной плотностью заряда σ=2 мкКл/м². В этом поле вдоль прямой, составляющей угол α = 60° с плоскостью, из точки 1 в точку 2, расстояние l между которыми равно 20 см, перемещается точечный электрический заряд Q=10 нКл. Определить работу A сил поля по перемещению заряда.

339. Тонкая квадратная рамка равномерно заряжена с линейной плотностью заряда t = 200 пКл/м. Опреде­лить потенциал j поля в точке пересечения диагоналей.

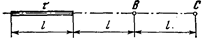340. На отрезке прямого провода равномерно распределен заряд с линейной плотностью τ=1 мкКл/м. Определить работу A сил поля по перемещению заряда Q=1 нКл из точки B в точку С.

341. Конденсатор емкостью C ₁=10 мкФ заряжен до напряжения U =10 В. Определить заряд на обкладках этого конденсатора после того, как параллельно ему был подключен другой, незаряженный, конденсатор ем­костью C ₂=20 мкФ.

342. Конденсаторы емкостью C ₁=5 мкФ и C ₂=10 мкФ заряжены до напряжений U ₁=60В и U ₂ = 100В соответственно. Определить напряжение на об­кладках конденсаторов после их соединения обкладками, имеющими одноименные заряды.

343. Два конденсатора емкостями C ₁ = 2 мкФ и C ₂=5 мкФ заряжены до напряжений U ₁ = 100 В и U ₂=150 В соответственно. Определить напряжение на об­кладках конденсаторов после их соединения обкладками, имеющими разноименные заряды.

344. Конденсаторы емкостями C ₁ = 2 мкФ, С ₂ = 5 мкФ и С ₃=10 мкФ соединены последовательно и находятся под напряжением U= 850 В. Определить на­пряжение и заряд на каждом из конденсаторов.

345. Два одинаковых плоских воздушных конденсато­ра емкостью C=100 пФ каждый соединены в батарею последовательно. Определить, на сколько изменится емкость C батареи, если пространство между пластинами одного из конденсаторов заполнить парафином.

346. Два конденсатора емкостями C ₁=5 мкФ и C ₂=8 мкФ соединены последовательно и присоединены к батарее с ЭДС e=80 В. Определить заряды Q₁ и Q₂ конденсаторов и разности потенциалов U ₁ и U ₂ между их обкладками.

347. Два металлических шарика радиусами R ₁ = 5 см и R ₂ = 10 см имеют заряды

Q₁ = 40 нКл и Q₂=-20 нКл соответственно. Найти энергию W, которая выделится при разряде, если шары соединить проводни­ком.

348. Плоский конденсатор состоит из двух круглых пластин радиусом R= 10 см каждая. Расстояние между пластинами d =2 мм. Конденсатор присоединен к источнику напряжения U =80 В. Определить заряд Q и напряженность Е поля конденсатора в двух случаях: а) диэлектрик — воздух; б) диэлектрик — стекло.

349. Пространство между пластинами плоского кон­денсатора заполнено двумя слоями диэлектрика: стекла толщиной d ₁ = 0,2 см и слоем парафина толщиной d ₂=0,3 см. Разность потенциалов между обкладками U =300 В. Определить напряженность Е поля и падение потенциала в каждом из слоев.

350. Плоский конденсатор с площадью пластин S =200 см² каждая заряжен до разности потенциалов U =2 кВ. Расстояние между пластинами d =2 см. Диэлект­рик - стекло. Определить энергию W поля конденсатора и плотность энергии w поля.

351. Уединенная металлическая сфера электроемкостью C=10 пф заряжена до потенциала φ=3 кВ. Определить энергию W поля, заключенного в сферическом слое, ограниченном сферой и концентрической с ней сферической поверхностью, радиус которой в три раза больше радиуса сферы.

352. Электрическое поле создано заряженной (Q=0,1 мкКл) сферой радиусом R=10cм. Какова энергия W поля, заключенная в объеме, ограниченном сферой и концентрической с ней сферической поверхностью, радиус которой в два раза больше радиуса сферы?

353. Уединенный металлический шар радиусом R ₁ =6 см несет заряд Q. Концентрическая этому шару поверхность делит простран­ство на две части (внутренняя конечная и внешняя бесконечная), так что энергии электрического поля обеих частей одинаковы. Опре­делить радиус R ₂ этой сферической поверхности.

354. Сплошной парафиновый шар радиусом R= 10 см заряжен равномерно по объему с объемной плотностью ρ=10 нКл/м³. Определить энергию W₁ электрического поля, сосредоточенную в самом шаре, и энергию W₂ вне его.

355. Эбонитовый шар равномерно заряжен по объему. Во сколько раз энергия электрического поля вне шара превосходит энергию поля, сосредоточенную в шаре?

356. Уединенная металлическая сфера электроемкостью C=4пФ заряжена до потенциала j =1 кВ. Определите энергию поля, заключенную в сферическом слое между сферой и концентрической с ней сферической поверхностью, радиус которой в 4 раза больше радиуса уединенной сферы.

357. Две концентрические проводящие сферы радиусами 20 см и 50 см заряжены соответственно одинаковыми зарядами по 100нКл. Определите энергию электростатического поля, заключенную внутри шара.

358. Сплошной шар из диэлектрика радиусом 5 см заряжен равномерно с объемной плотностью 10 нКл/м³. Определите энергию электростатического поля, заключенную в окружающем шар пространстве.

359. Металлический шар радиусом R=3 см несет заряд Q=20 нКл. Шар окружен слоем парафина толщиной d=9 см. Опре­делить энергию W электрического поля, заключенного в слое ди­электрика.

360. Металлический шар радиусом R=3 см несет заряд Q=20 нКл. Шар окружен слоем парафина толщиной d=2 см и слюды d=4 см. Определить энергию W электрического поля, заключенного в системе шар - диэлектрик.

361. Сила тока в проводнике сопротивлением R= 10 Oм за время t= 50 с равномерно нарастает от I ₁=5 А до I ₂=10 А. Определить количество теплоты Q, выделившееся за это время в проводнике.

362. За время t =20 с при равномерно возраставшей силе тока от нуля до некоторого максимума в проводнике сопротивлением R =5 Oм выделилось количество теплоты Q=4 кДж. Определить скорость нарастания силы тока, если сопротивление проводника R =5Oм.

363. Сила тока в проводнике сопротивлением R=10 Ом изменяется со временем по закону 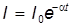, где I ₀=20 A, a=10² c^-1. Определить количество теплоты, выделившееся в проводнике за время t= 10^-2 с.

364. Сила тока в проводнике изменяется со временем по закону 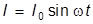. Найти заряд Q, проходящий через поперечное сечение проводника за время t, равное половине периода T, если начальная сила тока I ₀ = 10 A, цик­лическая частота w=50pс^-1.

365. В проводнике за время t =10 с при равномерном возрастании силы тока от I ₁ = 1 A до I ₂ = 2 A выдели­лось количество теплоты Q = 5 кДж. Найти сопротивление R проводника.

366. За время t= 8 с при равномерно возраставшей силе тока в проводнике сопротивлением R= 8 Oм выделилось количество теплоты Q = 500 Дж. Определить заряд q, проходящий в проводнике, если сила тока в начальный момент времени равна нулю.

367. За время t= 10 с при равномерно возрастающей силе тока от нуля до некоторого максимума в проводнике выделилось количество теплоты Q = 40 кДж. Определить среднюю силу тока < I > в проводнике, если его сопротивление R= 25 Oм.

368. Сила тока в цепи изменяется по закону 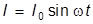. Определить количество теплоты, которое вы­делится в проводнике сопротивлением R= 10 Oм за вре­мя, равное четверти периода (от t =0 до t ₂=T/4, где Т = 10 с, I ₀=2 A).

369. Определить количество теплоты Q, выделившееся за время t =10 с в проводнике сопротивлением R =10 Oм, если сила тока в нем, равномерно уменьшаясь, изменилась от I ₁ = 10 A до I ₂=0.

370. Сила тока в цепи изменяется со временем по закону 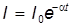. Определить количество теплоты, которое выделится в проводнике сопротивлением R =20 Oм за время, в течение которого ток уменьшится в е раз. Коэффициент a принять равным 2×10^-2 с^-1, I₀ =5 A.

371. Имеется N одинаковых гальванических элементов с ЭДС e₁ и внутренним сопротивлением r₁ каждый. Из этих элементов требуется собрать батарею, состоящую из нескольких параллель­но соединенных групп, содержащих по n последовательно соединен­ных элементов. При каком значении n сила тока I во внешней цепи, имеющей сопротивление R, будет максимальной? Чему будет равно внутреннее сопротивление r, батареи при этом значении n?

372. К источнику тока с ЭДС e = 1,5 В присоединили катуш­ку с сопротивлением R=0,1 Ом. Амперметр показал силу тока, рав­ную I₁=0,5A. Когда к источнику тока присоединили последовательно еще один источник тока с такой же ЭДС, то сила тока I₂ в той же катушке оказалась равной 0,4 А. Определить внутренние сопротивления r₁ и r₂ первого и второго источников тока.

373. Два одинаковых источника то­ка с ЭДС e = 1,2 В и внутренним сопротивлением r=0,4 Ом соединены, как показано на рис. а, б. Определить силу тока I в цепи и разность потенциа­лов U между точками А и В в первом и втором случаях.

374. Два элемента (e₁=l,2 В, r₁=0,l Ом; e₂=0,9 В, r₂=0,3 Ом) соединены одноименными полюсами. Сопротивление R соединительных проводов равно 0,2 Ом. Определить силу тока I в цепи.

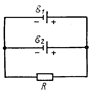
375. Две батареи аккумуляторов (e₁=10 В, r₁=l Ом; e₂=8 В, r₂=2 Ом) и реостат (R=6 Ом) соединены, как показано на рисунке. Найти силу тока в батареях и реостате.

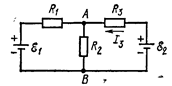376. Определить силу тока I₃ в резисторе сопротивлением R₃и напряжение U₃ на концах резистора, если e₁=4 В, e₂=3 В, R₁=2 Oм, R₂=6 Ом, R₃=1 Ом. Внутренними сопротивле­ниями источников тока пренебречь.

377. Два источника тока (e₁= 8B, r₁=2 Ом; e₂ =6 В, r₂=1,5 Ом) и реостат (R ==10 Ом) соединены, как показано на рисунке. Вычислить силу тока I, текущего через реостат.

378. Три батареи с ЭДС e₁=12 В, e₂=5 В и e₃=10В и одина­ковыми внутренними сопротивлениями r, равными 1 Ом, соединены между собой одноименными полюсами. Сопротивление соединитель­ных проводов ничтожно мало. Определить силы токов I, идущих че­рез каждую батарею.

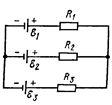379. Три источника тока с ЭДС e₁=11 В, e₂=4 В и e₃=6 В и три реостата с сопротивлениями R₁=5 Ом, R₂=10 Ом и R₃=2 Ом соединены, как показано на рисунке. Определить силы токов I в реостатах. Внутреннее сопротивление источника тока пренебрежи­мо мало.

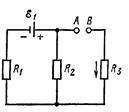380. Три сопротивления R₁=50м, R₂=1 Ом и R₃=3 Ом, а так­же источник тока с ЭДС e₁=1,4 В соединены, как показано на рисунке. Определить ЭДС e источника тока, который надо подключить в цепь между точками A и В, чтобы в сопротивлении R₃ шел ток силой I= 1 А в направлении, указанном стрелкой. Сопротив­лением источника тока пренебречь.

ПРИЛОЖЕНИЯ

Дата добавления: 2014-11-16