Контрольная работа 2

.

.

.

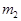Пример 5. Баллон содержит =80 г кислорода и = 320 г аргона. Давление смеси = 1 МПа, температу­ра =З00 К. Принимая данные газы за идеальные, определить объем V баллона.

Решение. По закону Дальтона, давление смеси равно сумме парциальных давлений газов, входящих в состав смеси. По уравнению Менделеева - Клапейрона, парциальные давления кислорода и 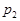аргона выра­жаются формулами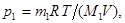

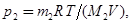
Следовательно, по закону Дальтона, давление смеси газов

,

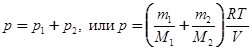откуда объем баллона

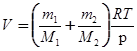. (1)

Произведем вычисления, учитывая, что кг/моль, кг/моль (см. табл. 9 При­ложения для O₂ и Ar):

.

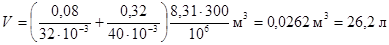Пример 6. Найти среднюю кинетическую энергию áe_вр ñ вращательного движения одной молекулы кислоро­да при температуре =350К, а также кинетическую энергию вращательного движения всех молекул кислорода массой m=4 г.

Решение. На каждую степень свободы молекулы газа приходится одинаковая средняя энергия

где k - постоянная Больцмана, T - термодинамическая температура газа. Так как вращательному движению двухатомной молекулы (молекула кислорода - двухатомная) соответствуют две степени свободы, то средняя энергия вращательного движения молекулы кислорода

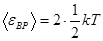. (1)

Кинетическая энергия вращательного движения всех молекул газа

. (2)

Число всех молекул газа N = N_An, (3)

где N_A - постоянная Авогадро; n- количество веще­ства.

Если учесть, что количество вещества n = m/M, где m- масса газа, M - молярная масса газа, то формула (3) примет вид

,

Подставив выражение N в формулу (2), получаем

. (4)

Произведем вычисления, учитывая, что для кислорода (O₂) 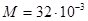кг/моль (см. табл. 9 Приложения):

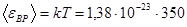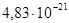Дж = Дж;

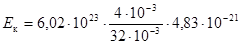Дж = 364 Дж.

Пример 7. Вычислить удельные теплоемкости при постоянном объеме 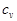и при постоянном давлении 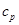неона и водорода, принимая эти газы за идеальные.

Решение. Удельные теплоемкости идеальных газов выражаются формулами

, (1)

, (2)

где - число степеней свободы молекулы газа, М - мо­лярная масса. Для неона (одноатомный газ) =3 и 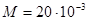кг/моль (см. табл. 9 Приложения). Произведем вычисления:

;

.

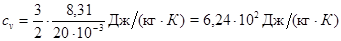Для водорода (двухатомный газ) =5 и М= кг/моль. Тогда

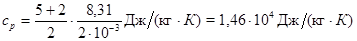
Пример 8. Вычислить удельные теплоемкости и смеси неона и водорода, если массовые доли неона и водорода составляют = 80 % и = 20 %. Значения удельных теплоемкостей газов взять из предыдущего примера.

Решение. Удельную теплоемкость смеси при постоянном объеме найдем следующим образом. Теплоту, необходимую для нагревания смеси на , выразим двумя способами:

, (1)

, (2)

где 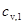- удельная теплоемкость неона; - удельная теплоемкость водорода.

Приравнявправые части (1) и (2) и разделив обе части полученного равенства на , получим . Отсюда

,

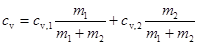или

где ,

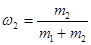
Рассуждая так же, получим формулу для вычисления удельной теплоемкости смеси при постоянном давлении:

Произведем вычисления:

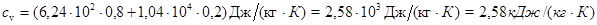
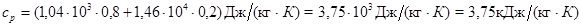
Пример 9. Определить среднюю длину свободного пробега молекул и число соударений за 1 с, происходящих между всеми молекула­ми кислорода, находящегося в сосуде емкостью 2 л при тем­пературе 27 °С и давлении 100 кПа.

Решение. Средняя длина свободного пробега молекул кисло­рода вычисляется по формуле 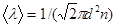(1)

где d — эффективный диаметр молекулы кислорода; п — число молекул в единице объема, которое можно определить из ура­внения

п = p/(kT), (2)

где k — постоянная Больцмана. Подставляя (2) в (1), имеем

(3)

Число соударенийZ, происходящих между всеми молекулами за 1 с, равно

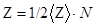(4)

где N — число молекул кислорода в сосуде объемом 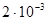м³,

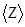- среднее число соударений одной молекулы за 1с. Число молекул в сосуде

N = nV (5)

Среднее число соударений молекулы за 1с равно

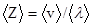(6)

где - средняя арифметическая скорость молекулы

(7)

Подставляя в (4) выражения (5),(6) и (7), находим

.

Подставляя числовые значения, получим

Ответ: Z =9×10²⁸ c^-1, álñ =3,56×10^-8 м.

Пример 10. Определить коэффициенты диффузии и внутреннего тре­ния азота, находящегося при температуре T=300 К и давлении 10⁵ Па.

Решение. Коэффициент диффузии определяется по формуле

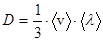
(1)

где ávñ - средняя арифметическая скорость молекул, равная

; (2)

álñ - средняя длина свободного пробега молекул. Для нахожде­ния álñ воспользуемся формулой(3)из решения примера 9:

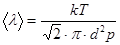(3)

Подставляя (2) и (3) в выражение (1),имеем

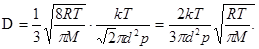(4)

Коэффициент внутреннего трения

(5)

где r — плотность газа при температуре 300 К и давлении 10⁵ Па. Для нахождения r воспользуемся уравнением состояния идеального газа. Запишем его для двух состояний азота — при нормальных условиях 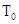=273 К, p₀ = 1,01×10⁵ Па и в условиях задачи:

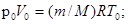
(6)

Учитывая, что 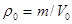, r = m /V, имеем

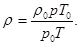(7)

Коэффициент внутреннего трения газа может быть выражен через коэффициент диффузии:

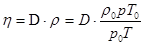(8)

Подставляя числовые значения в (4) и (8), получим

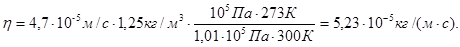
Ответ:

Пример 11. Кислород массой m = 2 кг занимает объем и находится под давлением 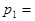0,2 МПа. Газ был нагрет сначала при постоянном давлении до объема 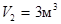, а затем при постоянном объеме до давления = 0,5 МПа. Найти изменение 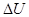внутренней энергии газа, совершенную им работу А и теплоту Q, передан­ную газу. Построить график процесса.

Решение. Изменение внутренней энергии газа

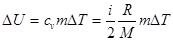; (1)

где i - число степеней свободы молекул газа (для двух­атомных молекул кислорода i =5); , - раз­ность температур газа в конечном (третьем) и начальном состояниях. Начальную и конечную температуру газа найдем из уравнения Менделеева - Клапейрона , откуда

Работа расширения газа при постоянном давлении выражается формулой

.

Работа газа, нагреваемого при постоянном объеме, равна нулю: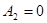

Следовательно, полная работа, совершаемая газом,

.

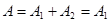Согласно первому началу термодинамики, теплота Q, переданная газу, равна сумме изменения внутренней энергии 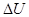и работы A

Q = DU + A.

Произведем вычисления, учтя, что для кислорода 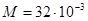кг/моль

(см. табл. 9 Приложения):

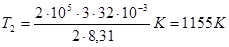
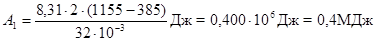
График процесса приведен на рисунке.

Пример 12. В цилиндре под поршнем находится водо­род массой 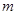=0,02кг при температуре З00 К. Водород сначала расширился адиабатно, увеличив свой объем в 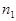=5 раз, а затем был сжат изотермически, причем объем газа уменьшился в 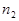= 5 раз. Найти температуру в конце адиабатного расширения и работу, совершаемую газом при этих процессах. Изобразить процесс графически.

Решение. Температуры и объемы газа, совершающего адиабатный процесс, связаны между собой соотношением

где 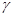- отношение теплоемкостей газа при постоянном давлении и постоянном объеме, .

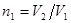Отсюда получаем следующее выражение для конечной температуры:

.

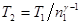Работа газа при адиабатном расширении может быть определена по формуле

,

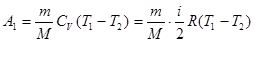где - молярная теплоемкость газа при постоянном объеме. Работа 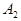газа при изотермическом процессе может быть выражена в ви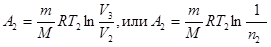де

,

где .

Произведем вычисления, учитывая, что для водорода как двухатомного газа 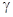=1,4, =5 и 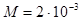кг/моль:

Так как =1,91 (находится логарифмированием), то ;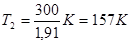

, .

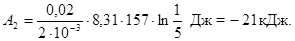Знак минус показывает, что при сжатии работа газа совершается над газом внешними силами. График процесса приведен на рисунке.

Пример 13. Объем аргона, находящегося при давлении 80 кПа, увеличился от 1 до 2л. На сколько изменится внутренняя энергия газа, если расширение производилось:

а) изобарно; б) адиабатно?

Решение. Применим первый закон термодинамики. Согласно этому закону, количество теплоты Q, переданное системе, рас­ходуется на увеличение внутренней энергии и на внешнюю механическую работу А:

Q = DU + A (1)

Величину можно определить, зная массу газа m, удельную теплоемкость при постоянном объеме и изменение температу­ры :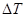

DU = m×c_V ×DT. (2)

Однако удобнее изменение внутренней энергии определять через молярную теплоемкость 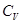, которая может быть выражена через число степеней свободы:

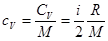(3)

Подставляя величину из формулы (3) в (2), получаем

. (4)

Изменение внутренней энергии зависит от характера процесса, при котором идет расширение газа. При изобарном расширении газа, согласно первому закону термодинамики, часть количества теплоты идет на изменение внутренней энергии , которая выражается формулой (4) Найти для аргона по формуле (4) нельзя, так как масса газа и температура в условии задачи не даны. Поэтому необходимо провести преобразование форму­лы (4).

Запишем уравнение Клапейрона — Менделеева для началь­ного и конечного состояний газа:

; ,

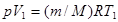или 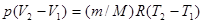. (5)

Подставив (5) в формулу (4), получим

. (6)

Это уравнение является расчетным для определения при изобарном расширении.

При адиабатном расширении газа теплообмена с внешней средой не происходит, поэтому Q = 0. Уравнение (1) запишется в виде

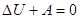. (7)

Это соотношение устанавливает, что работа расширения газа может быть произведена только за счет уменьшения внутренней энергии газа (знак минус перед ):

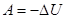. (8)

Формула работы для адиабатного процесса имеет вид

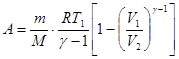, (9)

где 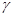— показатель степени адиабаты, равный отношению теплоемкостей: 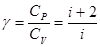. Для аргона — одноатомного газа (i =3) имеем .

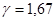Находим изменение внутренней энергии при адиабатном про­цессе для аргона, учитывая формулы (8) и (9):

. (10)

Для определения работы расширения аргона формулу (10) следует преобразовать, учитывая при этом параметры, данные в условии задачи. Применив уравнение Клапейрона — Менделе­ева для данного случая , получим выражение для подсчета изменения внутренней энергии:

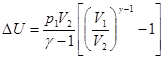. (11)

Подставляя числовые значения в (6) и (11), имеем:

а) при изобарном расширении ;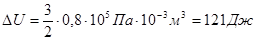

б) при адиабатном расширении

.

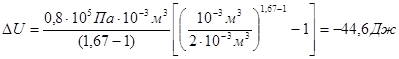Ответ: а) =121 Дж; б) = - 44,6Дж.

Пример 14. Тепловая машинаработает по обратимому циклу Карно. Температура теплоотдатчика К Определить термический КПД 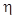цикла и температуру теплоприемника тепловой машины, если за счет каждого кило­джоуля теплоты, полученной от теплоотдатчика, машина совершает работу A=350 Дж.

Решение. Термический КПД тепловой машины показывает, какая доля теплоты, полученной от теплоотдатчика, превращается в механическую работу. Терми­ческий КПД выражается формулой h =A/Q₁,

где Q₁ - теплота, полученная от теплоотдатчика; А - работа, совершенная рабочим телом тепловой машины.

Зная КПД цикла, можно по формуле определить температуру охладителя : .

Произведем вычисления:

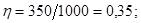
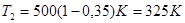
Пример 15. Определитьизменение энтропии 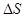при изотермическом расширении азота массой m =10 г, если давление газа уменьшилось от МПа до кПа.

Решение. Изменение энтропии, учитывая, что процесс изотермический,

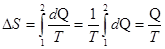. (1)

Согласно первому началу термодинамики, количество теплоты, полученное газом,

Q = A + DU. Для изотермического процесса DU = 0, поэтому Q = A. Работа газа в изотермическом процессе

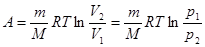. (2)

Подставив (2) в (1), найдем искомое изменение энтропии:

.

Вычисляя, получаем 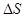= 2,06 Дж/К.

Пример 16. В сосуд с ртутью опущен открытый капилляр. Разность уровней ртути в сосуде и капилляре h = 37 мм. Принимая плотность ртути 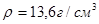, а ее поверхностное натяжение = 0,5 Н/м, определить радиус кривизны ртутного мениска в капилляре.

Решение. Избыточное давление, вызванное кривизной мениска,

,

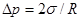где - поверхностное натяжение; R – радиус кривизны ртутного мениска. Так как ртуть – несмачивающая жидкость, то она в капилляре опускается на такую высоту, при которой давление столба жидкости (гидростатическое давление) уравновешивается избыточным давлением 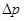, т. е.

,

где - плотность ртути; g – ускорение свободного падения. Отсюда искомый радиус кривизны ртутного мениска

.

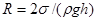Вычисляя, получим R = 2,03 мм.

Таблица вариантов

Вариант	Номера задач

201. Определить число N атомов в 1 кг водорода и массу одного атома водорода.

202. Определить количество вещества 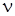водорода, заполняющего сосуд объемом

V=3 л, если концентрация молекул газа в сосуде .

203. Найти молярную массу M и массу m _M одной молекулы поваренной соли.

204. В сосуде вместимостью 1 л находится кислород массой 1г. Определить концентрацию молекул кислорода в сосуде.

205. За время t = 10 суток из стакана полностью испарилось m = 100 г воды. Сколько в среднем молекул вылетало с поверхности воды за 1 с?

206. Вычислить массу одной молекулы кислорода.

207. В сосуде вместимостью 5 л при нормальных условиях находится азот. Определить: 1) количество вещества 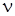; 2) массу азота; 3) концентрацию n его молекул в сосуде.

208. В сосуде вместимостью V = 0,3 л при температуре T = 290 K находится некоторый газ. На сколько понизится давление p газа в сосуде, если из него из-за утечки выйдет N = 10 ¹⁹ молекул?

209. В колбе вместимостью 240 см³ находится газ при температуре 290 К и давлении 50 кПа. Определите количество вещества газа (число молей) и число его молекул.

210. Во сколько раз плотность воздуха, заполняющего помещение зимой ( °С), больше его плотности летом ( °С)? Давление газа считать постоянным.

211. Два сосуда одинакового объема содержат кислород. В одном сосуде давление

p₁ = 2 MПа, и температура T₁ = 800 K, в другом p₂ = 2,5 MПа, T₂ =200 K. Сосуды соединили трубкой и охладили находящийся в них кислород до температуры T=200K. Определить установившееся в сосудах давление p.

212. В баллоне находится газ при температуре T₁ = 400 K. До какой температуры T₂ надо нагреть газ, чтобы его давление увеличилось в 1,5 раза?

213. В закрытом сосуде находится 10 кг при давлении 10⁷ Н/м². Найти, какое количество газа взяли из сосуда, если окончательное давление стало равным

2,5 10 ⁶ Н/м ²?

214. Азот массой 7 г находится под давлением p₁ = 0,1 МПа и температуре Т₁=290 К. Вследствие изобарного нагревания азот занял объем V₂ = 10 л. Определить: 1) объем V₁ газа до расширения; 2) температуру Т₂ газа после расширения; 3) плотности газа до и после расширения.

215. Баллон объемом V = 30 л содержит смесь водорода и гелия при температуре Т=300 К и давлении p = 828 кПа. Масса m смеси равна 24 г. Определить массу m₁ водорода и массу m₂ гелия.

216. По газопроводной трубе идет углекислый газ СО₂ при давлении p=3,9×10⁵Н/м² и температуре t=7⁰C. Какова скорость движения газа в трубе, если за t = 10 мин протекает m = 2 кг газа и площадь сечения канала трубы S=5см²? M_r co₂ =44.

217. Сосуд емкостью разделен пополам полупроницаемой перегородкой. В одну половину сосуда введен водород массой m₁ = 2 г и азот массой m₂ = 28 г, в другой половине вакуум. Через перегородку может диффундировать только водород. Во время процесса поддерживается температура Т = 373 К. Какие давления установятся в обеих частях сосуда?

218. Сколько гелия потребуется для наполнения воздушного шара диаметром

d = 10 м, чтобы шар смог поднять груз весом Q = 980 Н при нормальном атмосферном давлении и температуре Т = 290 K? Объемом груза пренебречь.

219. Какой объем V занимает смесь газов - азота массой m₁ = 1 кг и гелия массой

m₂= 1 кг – при нормальных условиях?

220. В сосуде объемом V = 0,01 м³ содержится смесь газов – азота массой m₁=7г и водорода массой m₂ = 1 г – при температуре Т = 280 K. Определить давление p смеси газов.

221. Найдите полную кинетическую энергию 10²⁴ молекул кислорода и давление, которое они оказывают на стенки сосуда, если они занимают объем 10 л при температуре 300 К.

222. Найдите температуру углекислого газа, если средняя энергия вращательного движения одной молекулы равна 1,6×10^-20 Дж.

223. Азот массой m = 10 г находится при температуре Т= 290 К. Определить:

1) среднюю кинетическую энергию одной молекулы азота; 2) среднюю кинетическую энергию вращательного движения всех молекул азота. Газ считать идеальным.

224. Кислород массой m = 1кг находится при температуре Т = 320 К. Определить:

1) внутреннюю энергию молекул кислорода; 2) среднюю кинетическую энергию вращательного движения молекул кислорода. Газ считать идеальным.

225. Определить внутреннюю энергию U водорода, а также среднюю кинетическую энергию молекулы 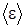этого газа при температуре Т=300К, если количество вещества ν этого газа равно 0,5 моль.

226. В закрытом сосуде находится смесь азота массой m ₁ = 56 г и кислорода массой m ₂ = 64 г. Определить изменение внутренней энергии этой смеси, если ее охладили на 20°.

227. Определить среднюю арифметическую скорость < v > молекул газа, если их средняя квадратичная скорость < v _КВ > = 1км /c.

228. Определить среднюю квадратичную скорость < v _КВ > молекулы газа, заключенного в сосуд вместимостью V = 2 л под давлением p = 200 кПа. Масса газа m = 3г.

229. Найдите концентрацию молекул кислорода, если их средняя квадратичная скорость равна 400 м/с, а давление 5×10⁴ Па.

230. Взвешенные в воздухе мельчайшие пылинки движутся так, как если бы они были очень крупными молекулами. Определите среднюю квадратичную скорость пылинки массой 10^-2 г, если температура воздуха 300 К.

231. Считая азот идеальным газом, определить его удельную теплоемкость:

1) для изобарного процесса; 2) для изохорного процесса.

232. Определить удельные теплоемкости c_v и c_p, если известно, что некоторый газ при нормальных условиях имеет удельный объем V =5,67м³_./кг. Какой это газ?

233. Определить удельные теплоемкости c_V и c_P смеси углекислого газа массой

m ₁ = 3 г и азота массой m ₂ = 4 г.

234. Вычислить удельные теплоемкости газа, зная, что его молярная масса

М = 4 10 ^-3 кг/ моль и отношение теплоемкостей Cp / Cv = 1,67.

235. Трехатомный газ под давлением p = 240 кПа и температуре t = 20°C занимает объем V = 10 л. Определить теплоемкость Cp этого газа при постоянном давлении.

236. Разность удельных теплоемкостей 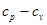некоторого двухатомного газа равна 260 Дж/(кг×К). Найти молярную массу М газа и его удельные теплоемкости c_P и c_V.

237. Определить удельную теплоемкость смеси газов, содержащей

V₁=5 л водорода и V₂=3 л гелия. Газы находятся при одинаковых условиях.

238. Определить удельную теплоемкость смеси кислорода и азота, если количество вещества 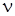₁ первого компонента равно 2 моль, а количество вещества 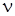₂ второго равно 4 моль.

239. В баллоне находятся аргон и азот. Определить удельную теплоемкость смеси этих газов, если массовые доли аргона w₁ и азота w₂ одинаковы и равны 0,5.

240. Смесь газов состоит из хлора и криптона, взятых при одинаковых условиях и в равных объемах. Определить удельную теплоемкость смеси.

241. В сосуде емкостью 1 л содержится кислород массой m = 32 г. Определить среднее число соударений молекул в секунду при температуре T = 100 K.

242. Определить среднюю длину и среднюю продолжительность свободного пробега молекул водорода при температуре T = 400 K и давлении p =1,38 Па.

243. Определить коэффициент диффузии гелия при давлении p= 10⁶ Па и температуре 27°C.

244. Определить коэффициент внутреннего трения кислорода при температуре

T = 400 K.

245. В сосуде емкостью 5 л содержится 40 г гелия. Определить среднее число соударений молекул в секунду при температуре T = 400 K.

246. Средняя длина свободного пробега молекул кислорода при температуре 300 К и давлении 0,1 МПа равна 200 нм. Найдите эффективный диаметр молекулы кислорода.

247. Средняя длина свободного пробега атомов гелия при нормальных условиях равна 180 нм. Найдите коэффициент диффузии гелия.

248. Определите среднее число столкновений одной молекулы азота за 1 с при нормальных условиях, если коэффициент вязкости азота при этих условиях

h = 1,8×10^-5 Па×с.

249. Найдите коэффициент теплопроводности гелия при нормальных условиях. Эффективный диаметр молекулы гелия 0,20 нм.

250. Идеальный газ совершил процесс, в результате которого его давление возросло в n раз. Как и во сколько раз изменились средняя длина свободного пробега и среднее число столкновений каждой молекулы в единицу времени, если процесс изохорный?

251. Кислород массой m = 32 г находится в закрытом сосуде под давлением

p = 0,1 MПа при температуре T = 290 K. После нагревания давление в сосуде повысилось в 4 раза. Определить: 1) объем сосуда; 2) температуру, до которой газ нагрели; 3) количество теплоты, сообщенное газу.

252. Некоторый газ массой 1кг находится при температуре T = 300 K и под давлением p₁ = 0,5 МПа. В результате изотермического сжатия давление газа увеличилось в 2 раза. Работа, затраченная на сжатие А = - 432 кДж. Определить:

1) какой это газ; 2) первоначальный удельный объем газа.

253. Азот массой 50 г находится при температуре T₁ = 280 K.В результате изохорного охлаждения его давление уменьшилось в n = 2 раза, а затем в результате изобарного расширения температура газа в конечном состоянии стала равной первоначальной. Определить: 1) работу, совершенную газом; 2) изменение внутренней энергии газа.

254. Работа расширения некоторого идеального двухатомного газа составляет

А = 2 кДж. Определить количество подведенной к газу теплоты, если процесс протекал: 1) изотермически; 2) изобарно.

255. Азот массой m = 1кг занимает при температуре T ₁ = 300K объем V₁ = 0,5м³. В результате адиабатического сжатия давление газа увеличилось в 3 раза. Определить: 1) конечный объем газа; 2) его конечную температуру; 3) изменение внутренней энергии газа.

256. Азот массой 500 г находящийся под давлением p₁= 1MПа при температуре t₁=127 °C, подвергли изотермическому расширению, в результате которого давление газа уменьшилось в n = 3 раза. После этого газ подвергли адиабатическому сжатию до начального давления, а затем он был изобарно сжат до начального объема. Построить график цикла и определить работу, совершенную газом за цикл.

257. Азот массой m = 14 г сжимают изотермически при температуре T = 300 K от давления p₁ = 100 кПа до p₂ = 500 кПа. Определить: 1) изменение внутренней энергии газа; 2) работу сжатия; 3) количество выделившейся теплоты.

258. При адиабатическом расширении кислорода (v = 2 моль), находящегося при нормальных условиях, его объем увеличился в n=3 раза. Определить: 1) изменение внутренней энергии газа; 2) работу расширения газа.

259. Кислород массой 10 г, находящийся при температуре 370 К, подвергли адиабатическому расширению, в результате которого его давление уменьшилось в n=4 раза. В результате последующего изотермического процесса газ сжимается до первоначального давления. Определить: 1) температуру газа в конце процесса;

2) количество теплоты, отданное газом; 3) приращение внутренней энергии газа;

4) работу, совершенную газом.

260. Какая доля w₁ количества теплоты Q, подводимого к идеальному двухатомному газу при изобарном процессе, расходуется на увеличение DU внутренней энергии газа и какая доля w₂ - на работу A расширения? Рассмотреть три случая, если газ:

1) одноатомный; 2) двухатомный; 3) трехатомный.

261. Идеальный газ, совершающий цикл Карно, 70 % количества теплоты, полученной от нагревателя, отдает холодильнику. Количество теплоты, получаемое от нагревателя, равно 5 кДж. Определить: 1) термический к.п.д. цикла; 2) работу, совершенную при полном цикле.

262. Идеальный газ совершает цикл Карно. Газ получил от нагревателя количество теплоты 5,5 к Дж и совершил работу 1,1кДж. Определить: 1) термический к.п.д. цикла; 2) отношение температур нагревателя и холодильника.

263. Идеальный газ совершает цикл Карно, термический к.п.д. которого равен 0,4. Определить работу изотермического сжатия газа, если работа изотермического расширения составляет 400 Дж.

264. Идеальный газ совершает цикл Карно. Температура нагревателя T₁=500К, холодильника Т₂=300 К. Работа изотермического расширения газа составляет 2кДж. Определить: 1) термический к.п.д. цикла; 2) количество теплоты, отданное газом при изотермическом сжатии холодильнику.

265. Многоатомный идеальный газ совершает цикл Карно, при этом в процессе адиабатического расширения объем газа увеличивается в n = 4 раза. Определить термический к.п..д. цикла.

266. При нагревании двухатомного идеального газа (v = 3 моль) его термодинамическая температура увеличилась в n=2 раза. Определить изменение энтропии, если нагревание происходит: 1) изохорно; 2) изобарно.

267. Идеальный газ (v = 2 моль) сначала изобарно нагрели, так что объем увеличился в n₁ = 2 раза, а затем изохорно охладили, так что давление его уменьшилось в n₂ = 2 раза. Определить приращение энтропии в ходе указанных процессов.

268. Азот массой 28 г адиабатически расширили в n = 2 раза, а затем изобарно сжали до первоначального объема. Определить изменение энтропии газа в ходе указанных процессов.

269. Кислород массой 2 кг увеличил свой объем в 5 раз, один раз изотермически, другой раз адиабатически. Каково изменение энтропии в этих двух случаях?

270. Водород массой 100 г был изобарически нагрет так, что его объем увеличился в n раз, затем он был изохорически охлажден так, что его давление уменьшилось в n раз. Найти изменение энтропии для n = 3.

271. При определении силы поверхностного натяжения капельным методом число капель глицерина, вытекающего из капилляра, составляет n = 50. Общая масса глицерина m = 1 г, а диаметр шейки капли в момент отрыва d = 1мм. Определить поверхностное натяжение s глицерина.

272. Определить радиус R капли спирта, вытекающей из узкой вертикальной трубки радиусом r = 1мм. Считать, что в момент отрыва капля сферическая. Поверхностное натяжение спирта s = 22 мН /м, а его плотность r = 0,8 г /см ³.

273. Считая процесс образования мыльного пузыря изотермическим, определить работу А, которую надо совершить, чтобы увеличить его диаметр от d ₁ = 6 мм до

d ₂ = 60 мм. Поверхностное натяжение мыльного пузыря раствора принять равным 40 мН /м.

274. Две капли воды радиусом r = 1 мм каждая слились в одну большую каплю. Считая процесс изотермическим, определить изменение поверхностной энергии при этом слиянии, если поверхностное натяжение воды s = 73 мН /м.

275. Давление воздуха внутри мыльного пузыря на Dp = 200 Па больше атмосферного. Определить диаметр d пузыря. Поверхностное натяжение мыльного раствора s = 40 мН / м.

276. Воздушный пузырек диаметром d = 0,02 мм находится на глубине h = 25 см под поверхностью воды. Определить давление воздуха в этом пузырьке. Атмосферное давление принять нормальным. Поверхностное натяжение воды s = 73 мН / м, а ее плотность r = 1 г /см ³.

277. Ртуть массой 3 г помещена между двумя параллельными стеклянными пластинками. Определить силу, которую необходимо приложить, чтобы расплющить каплю до толщины d = 0,1 мм. Ртуть стекло не смачивает. Плотность ртути

r=13,6 г/см ³, а ее поверхностное натяжение s = 0,5 Н/м.

278. Капилляр вертикально погружен в воду. Определить радиус кривизны мениска, если высота столба воды в трубке h = 20 мм. Плотность воды r=1г/см³, поверхностное натяжение s = 73 мН / м.

279. Капилляр внутренним радиусом 0,5 мм опущен в жидкость. Определить массу жидкости, поднявшейся в капилляр, если ее поверхностное натяжение равно

60 мН/м.

280. Широкое колено U – образного манометра имеет диаметр d₁ = 2 мм,

узкое – d₂ = 1 мм. Определить разность Dh уровней ртути в обоих коленах, если поверхностное натяжение ртути s = 0,5 Н/м, плотность ртути r = 13,6 г/см³, а краевой угол q равен 138 °. [А1]

Дата добавления: 2014-11-16