Основные физические величины и законы

Задачи

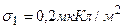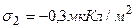3.01. Две параллельные плоскости, заряженные с поверхностными плотностями и , находятся на расстоянии 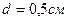друг от друга. Определить разность потенциалов между плоскостями.

3.02. Расстояние d между двумя точечными зарядам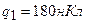и и

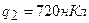равно 60 см. Определить точку, в которую нужно поместить третий заряд 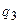так, чтобы система зарядов находилась в равновесии. Определить величину и знак заряда. Устойчивое или неустойчивое будет равновесие?

3.03. На бесконечном тонкостенном цилиндре диаметром 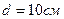равномерно распределен заряд с поверхностной плотностью 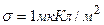. Определить напряженность поля в точке, отстоящей от поверхности цилиндра на .

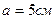3.04. Два одинаковых металлических заряженных шара находятся на расстоянии 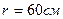. Сила отталкивания шаров 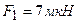. После того как шары привели в соприкосновение и удалили друг от друга на прежнее расстояние, сила отталкивания возросла и стала равной 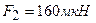. Вычислить заряды 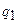и , которые были на шарах до их соприкосновения. Диаметр шаров считать много меньшим расстояния между ними.

3.05. Электрон, обладающий кинетической энергией 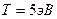, влетел в однородное электрическое поле в направлении силовых линий поля. Какой скоростью будет обладать электрон, пройдя в этом поле разность потенциалов ?

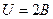3.06. Определить потенциальную энергию системы двух точечных зарядов 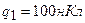и 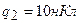, находящихся на расстоянии 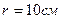друг от друга.

3.07. Поле образовано бесконечной равномерно заряженной плоскостью с поверхностной плотностью заряда 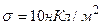. Определить разность потенциалов U двух точек поля, отстоящих от плоскости на 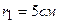и .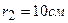

3.08. Пылинка массой 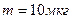, несущая на себе заряд 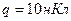, влетела в электрическое поле в направлении силовых линий. После прохождения разности потенциалов 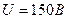пылинка имела скорость 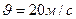. Определить скорость пылинки до того, как она влетела в поле.

3.09. Три одинаковых капли ртути, заряженных до потенциала 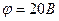, сливаются в одну. Каков потенциал образовавшейся капли?

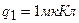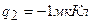3.10. Точечные заряды и находятся на расстоянии 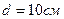друг от друга. Определить напряженность поля в точке, удаленной на 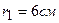от первого и, 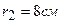от второго заряда. Определить также силу, действующую в этой точке на точечный заряд .

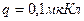3.11. Между пластинами плоского конденсатора вложена тонкая слюдяная пластинка. Какое давление испытывает эта пластинка при напряженности электрического поля ?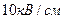

3.12. Плоский конденсатор с площадью пластин 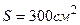каждая заряжен до разности потенциалов 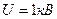. Расстояние между пластинами

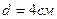. Диэлектрик – стекло. Определить энергию W поля конденсатора и плотность ω энергии поля.

3.13. Расстояние между пластинами плоского конденсатора 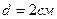, разность потенциалов 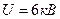. Заряд каждой пластины 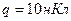. Определить энергию W поля конденсатора и силу F взаимного притяжения пластин.

3.14. Емкость плоского конденсатора 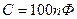. Диэлектрик – фарфор. Конденсатор зарядили до разности потенциалов 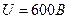и отключили от источника напряжения. Какую работу нужно совершить, чтобы вынуть диэлектрик из конденсатора?

3.15. Плоский конденсатор состоит из двух круглых пластин радиусом

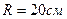каждая. Расстояние между пластинами 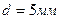. Конденсатор присоединен к источнику напряжения 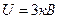. Определить заряд и напряженность поля конденсатора, если диэлектриком будут: а) воздух; б) стекло.

3.16. Пластины плоского конденсатора площадью 100 см² каждая притягиваются друг к другу с силой 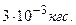Пространство между пластинами заполнено слюдой. Найти: 1). заряды, находящиеся на пластинах, 2). напряженность поля между пластинами, 3). энергию в единице объема поля.

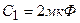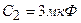3.17. Два конденсатора емкостью и соединены последовательно и присоединены к батарее э. д. с. 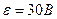. Определить заряд каждого конденсатора и разность потенциалов между его обкладками.

3.18. Пространство между пластинами плоского конденсатора заполнено двумя слоями диэлектриков: слоем стекла толщиной 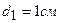и слоем парафина толщиной 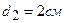. Разность потенциалов между обкладками 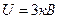. Определить напряженность поля и падение потенциала в каждом из слоев.

3.19. Разность потенциалов между пластинами плоского конденсатора площадью 100 см² каждая равна 280 В. Поверхностная плотность заряда на пластинах 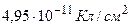. Найти: 1). напряженность поля внутри конденсатора, 2). расстояние между пластинами, 3). скорость, которую получит электрон, пройдя в конденсаторе путь от одной пластины до другой, 4). энергию конденсатора.

3.20. Плоский воздушный конденсатор с площадью пластин 100 см² и расстоянием между ними 1 мм заряжен до 100 В. Затем пластины раздвигаются до расстояния 25 мм. Найти энергию конденсатора до и после раздвижения пластин, если источник напряжения перед раздвижением отключается.

3.21. Имеется 120-вольтовая лампочка мощностью 40 Вт. Какое добавочное сопротивление надо включить последовательно с лампочкой, чтобы она давала нормальный накал при напряжении в сети 220 В? Сколько метров нихромовой проволоки диаметром 0,3 мм надо взять, чтобы получить такое сопротивление?

3.22. В сеть с напряжением 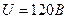включили катушку с сопротивлением 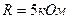и вольтметр, соединенные последовательно. Показание вольтметра 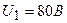. Когда катушку заменили другой, вольтметр показал 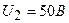. Определить сопротивление другой катушки.

3.23. Определить число электронов, проходящих в секунду через единицу площади поперечного сечения железной проволоки длиной 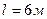при напряжении на ее концах .

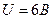3.24. Сила тока в проводнике равномерно увеличивается от нуля до некоторого максимального значения в течение времени 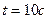. За это время в проводнике выделилась теплота 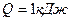. Определить скорость нарастания тока в проводнике, если сопротивление его .

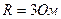3.25. От батареи, э. д. с. которой 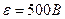, требуется передать энергию на расстояние 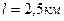. Потребляемая мощность 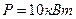: Найти минимальные потери мощности в сети, если диаметр медных подводящих проводов .

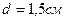3.26. Э. д. с. батареи 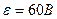, внутреннее сопротивление 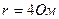. Внешняя цепь потребляет мощность 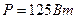. Определить силу тока I в цепи, напряжение U, под которым находится внешняя цепь, и ее сопротивление .

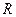3.27. Э. д. с. батареи 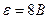. При силе тока 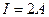к. п. д. батареи 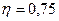. Определить внутреннее сопротивление 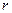батареи.

3.28. При внешнем сопротивлении 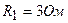сила тока в цепи 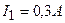, при сопротивлении 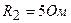сила тока 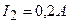. Определить силу тока короткого замыкания источника э. д. с.

3.29. По проводнику сопротивлением 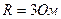течет равномерно возрастающий ток. За время 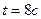в проводнике выделилась теплота 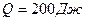. Определить заряд q, протекший за это время по проводнику. В момент времени, принятый за начальный, ток в проводнике был равен нулю.

3.30. Элемент замыкают сначала на внешнее сопротивление 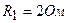, а затем на внешнее сопротивление 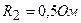. Найти э.д.с. элемента и его внутреннее сопротивление, если известно, что в каждом из этих случаев мощность, выделяемая во внешней цепи, одинакова и равна 2,54 Вт.

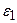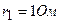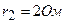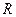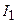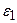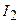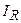3.31. В схеме рисунок 12 и – два элемента с равными э.д.с. 2 В. Внутренние сопротивления этих элементов равны соответственно и . Чему равно внешнее сопротивление если сила тока , текущего через , равна 1 А? Найти силу тока , идущего через . Найти силу тока , идущего через сопротивление .

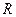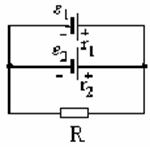
Рисунок 12.

3.32. Определить силу тока в каждом элементе и напряжение на зажимах сопротивления 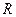(см.рисунок 3 31), есл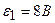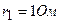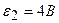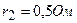и , , , и .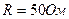

3.33. Какая разность потенциалов получается на зажимах двух элементов, включенных параллельно, если их э.д.с. равны соответственно 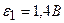и 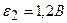и внутренние сопротивления 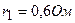и ?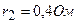

3.34. Определить силы токов на всех участках электрической цепи (см. рисунок 13), если 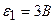, , 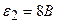, , 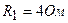, 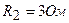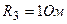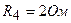. Внутренними сопротивлениями источников тока пренебречь.

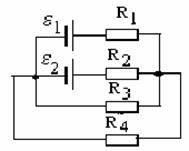
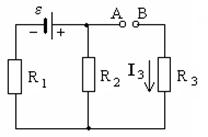
Рисунок 13. Рисунок 14.

3.35. Три сопротивления 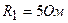, 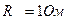и 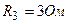, а также источник тока 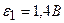соединены, как показано на рисунке 14. Определить э. д. с. источника, который надо подключить в цепь между точками A и В, чтобы в сопротивлении R₃ шел ток силой 1А в направлении, указанном стрелкой. Сопротивлением источников тока пренебречь.

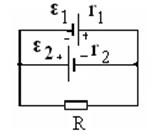3.36. Определить разность потенциалов между точками А и В (рисунок 15), если 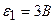, , 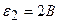, , 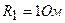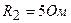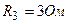. Внутренними сопротивлениями источников тока пренебречь.

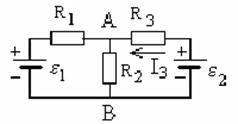
Рисунок 15. Рисунок 16.

3.37. Определить силу тока в сопротивлении R₃(рисунок 15) и напряжение на концах этого сопротивления, если , , 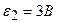, , 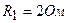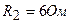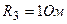. Внутренними сопротивлениями источников тока пренебречь.

3.38. Два источника тока 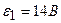с внутренним сопротивлением 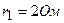и 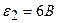с внутренним сопротивлением 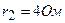, а также реостат 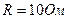соединены, как показано на рисунке 16. Определить силы тока в реостате и в источниках тока.

3.39. В схеме рисунка 17 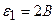, , 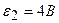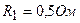и падение потенциала на сопротивление 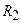(ток через 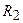направлен сверху вниз) равно 1 В. Найти показание амперметра. Внутренним сопротивлением элементов и амперметра пренебречь.

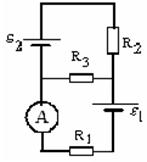
Рисунок 17.

3.40. В схеме рисунка 17 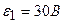, , 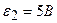, 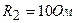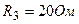. Через амперметр идет ток 1 А, направленный от 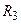к 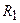. Найти сопротивление 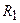. Сопротивлением батареи и амперметра пренебречь.

ЭЛЕКТРОМАГНЕТИЗМ

Закон Ампера

,

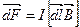где 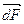– сила, с которой магнитное поле действует на элемент длины проводника 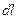с током 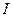, вектор 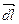совпадает с направлением тока, 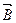– вектор магнитной индукции.

В скалярном виде

,

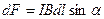где 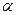– угол между векторам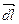и и .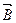

Сила Лоренца

,

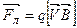где 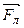– сила, действующая на заряд , движущийся в магнитном поле со скоростью 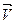(сила Лоренца).

В скалярном виде

,

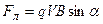где 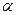– угол между 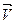и .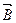

Связь магнитной индукции 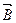и напряженности 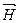магнитного поля

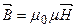
где 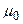– магнитная постоянная, – магнитная проницаемость среды.

Закон Био-Савара-Лапласа

,

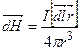где 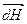– напряженность магнитного поля, создаваемого элементом длины 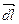проводника с током 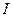; 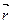– радиус-вектор, приведенный от 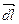к точке, в которой определяется напряженность поля.

В скалярном виде

,

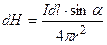где 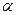– угол между векторам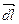и и .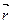

Из закона Био-Савара-Лапласа следуют формулы, определяющие:

1). напряженность магнитного поля в центре кругового проводника радиуса 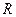с током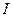

;

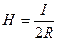2). Напряженность магнитного поля, создаваемого отрезком прямолинейного проводника с током, в точке, отстоящей от проводника на расстоянии 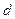, и определяемой углам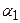и и 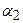между направлением тока и радиус-векторами из начала и конца отрезка в эту точку

;

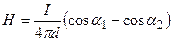3). Напряженность магнитного поля, создаваемого «бесконечно длинным» (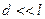) проводником с током 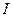на расстоянии 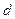от него

;

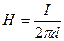4). Напряженность магнитного поля внутри соленоида, имеющего 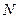витков, длину 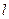, много большую диаметра соленоида D

.

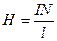Поток вектора магнитной индукции (магнитный поток) через произвольную поверхность

,

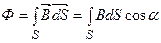где 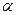– угол между векторам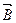и и 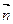, 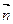– вектор нормали к площадке .

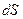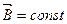Поток вектора магнитной индукции через площадку в однородном () магнитном поле соответственно

.

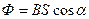Закон электромагнитной индукции

,

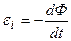где 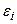– э.д.с. индукции.

Э.д.с. самоиндукции

,

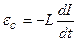где 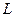– индуктивность контура

,

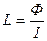где – магнитный поток, создаваемый в контуре током .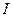

Индуктивность соленоида (тороида)

,

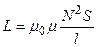где 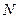– число витков соленоида, 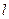– его длина, – площадь сечения.

Работа по перемещению проводника с током в магнитном поле

,

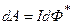где 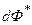– магнитный поток, пересеченный движущимся проводником.

Работа по перемещению замкнутого контура с током в магнитном поле

,

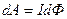где 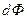– изменение магнитного потока, сцепленного с контуром.

Работа перемещения контура при неизменном токе в нем

,

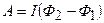где 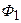и 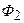– начальный и конечный магнитный потоки через контур.

Энергия магнитного поля, создаваемого током в замкнутом контуре, по которому течет ток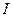

.

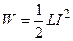Объемная плотность энергии

.

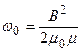Пример 1. В однородном магнитном поле с индукцией 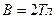движется протон. Траектория его движения представляет собой винтовую линию с радиусом 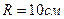и шагом 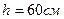. Определить кинетическую энергию протона.

Дано: ; ; ;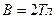

; .

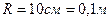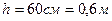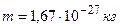Найти: .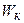

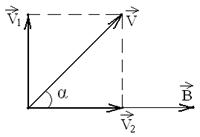
Рисунок 18.

Решение. Кинетическая энергия протона (при )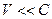

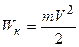. (1.1)

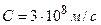– скорость света.

Заряженная частица движется в магнитном поле по винтовой линии в случае, когда ее скорость 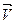составляет с направлением вектора индукции 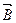угол 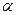, не равный 90⁰. В таком случае частица движется по окружности в плоскости, перпендикулярной линиям индукции 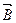со значением составляющей скорости 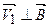и одновременно поступательно вдоль силовых линий 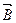со значением составляющей скорости .

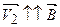Как видно из рисунка 4.1 ; .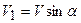

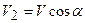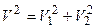. (1.2)

Согласно второму закону Ньютона

.

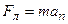Сила Лоренца перпендикулярна вектору скорости 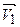и сообщает протону нормальное ускорение .

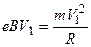Отсюда

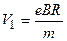, (1.3)

где 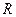– радиус окружности.

Шаг винтовой линии – это расстояние, пройденное протоном со скоростью 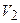вдоль силовой линии 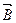за время, равное периоду его вращения 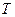по окружности

.

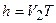Так как 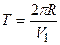, то .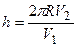

Отсюда

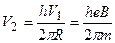. (1.4)

Подставляя формулы (1.3) и (1.4) в уравнение (1.2), находим

.

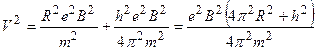Отсюда .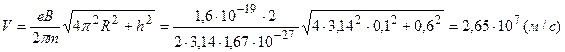

Как видно, .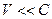

Таким образом, для кинетической энергии протона по формуле (1.1) получаем значение

.

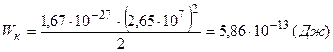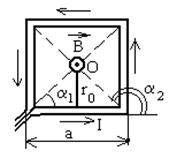Пример 2. По проводу, согнутому в виде квадрата со стороной 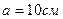, течет ток силой 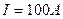. Найти магнитную индукцию 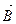в точке пересечения диагоналей квадрата.

Дано: ;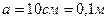

.

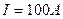Найти: .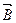

Рисунок 19.

Решение. Расположим квадратный виток в плоскости чертежа (рисунок 19). Согласно принципу суперпозиции магнитных полей магнитная индукция 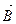поля квадратного витка будет равна геометрической сумме магнитных индукций полей, создаваемых каждой стороной квадрата в отдельности:

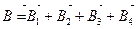. (2.1)

В точке О пересечения диагоналей квадрата все векторы индукции будут направлены перпендикулярно плоскости витка «к нам». Кроме того, из соображений симметрии следует, что абсолютные значения этих векторов одинаковы: В₁ = В₂ = Вз = В₄. Это позволяет векторное равенство (2.1) заменить скалярным равенством

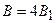(2.2)

Магнитная индукция В₁ поля, создаваемого отрезком прямолинейного провода с током, выражается формулой

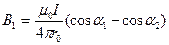. (2.3)

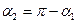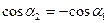Учитывая, что и (рисунок 4.2), формулу (2.3) можно переписать в виде

.

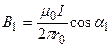Подставив это выражение В₁ в формулу (2.2), найдем

.

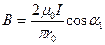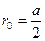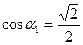Заметим, что и (так как 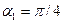), получим

.

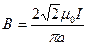Подставим в эту формулу числовые значения физических величин и произведем вычисления:

.

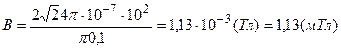Пример 3. В однородном магнитном поле с индукцией 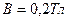равномерно вращается катушка, содержащая 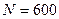витков, с частотой 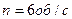. Площадь поперечного сечения катушки 100 см². Ось вращения перпендикулярна оси катушки и направлению магнитного поля. Определить максимальную э.д.с. индукции вращающейся катушки.

Дано: ; ; ; .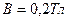

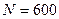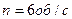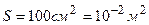Найти: .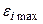

Решение. Согласно закону электромагнитной индукции

.

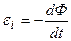суммарный магнитный поток через все витки катушки (потокосцепление катушки)

,

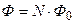где 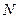– число витков, 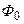– магнитный поток, пронизывающий каждый отдельный виток.

При произвольном расположении катушки относительно магнитного поля

.

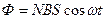Учитывая, что круговая частота 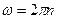, получим

.

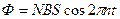Тогда

.

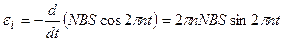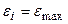при .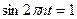

Поэтому .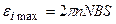

Подставляя численные значения величин получим

.

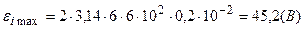Пример 4. Виток, в котором поддерживается постоянная сила тока

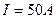, установился в однородном магнитном поле (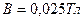). Диаметр витка 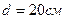. Какую работу А нужно совершить, чтобы повернуть виток относительно оси, совпадающей с диаметром, на угол ?

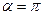Дано: ; ; ; ; .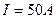

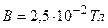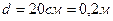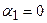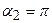Найти: .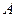

Решение. Работу поворота витка с постоянным током определим по формуле

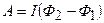. (4.1)

магнитный поток через виток в произвольном положении

,

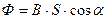где 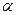– угол между нормалью 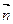к плоскости витка и направлением вектора магнитной индукции .

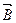В начальном (равновесном) положении нормаль 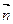совпадает с направлением вектора 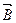, то есть .

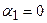После поворота, по условию задачи, .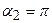

Таким образом

;

.

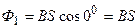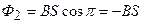Подставляя эти выражении в уравнение (4.1), получим

.

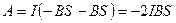И так как площадь витка равна 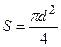, то окончательно имеем

.

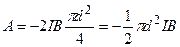Подставляя численные значения величин, получим

.

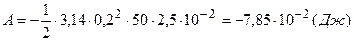Работа внешних сил против сил магнитного поля.

Пример 5. Соленоид имеет длину 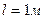и сечение 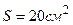. При некоторой силе тока, протекающего по обмотке, в соленоиде создается магнитный поток 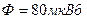. Чему равна энергия W магнитного поля соленоида? Сердечник выполнен из немагнитного материала, и магнитное поле во всем объеме однородно.

Дано: ; ; ;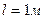

; .

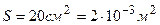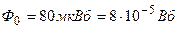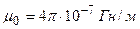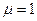Найти: .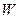

Решение. Энергию однородного магнитного поля определим по формуле

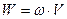, (5.1)

где – объем соленоида:

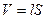(5.2)

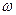– объемная плотность энергии магнитного поля

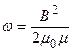. (5.3)

Магнитный поток через каждый виток соленоида

,

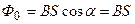так как нормаль 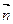к плоскости витков совпадает по направлению с вектором 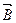и, соответственно, 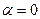и .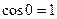

Отсюда

.

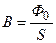Подставляя это выражение в уравнение (5.3), получим

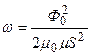. (5.3)

С учетом формул (5.2) и (5.3) уравнение (5.1) принимает вид

.

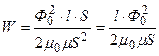Подставляя численные значения величин, получаем

.

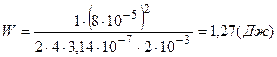Дата добавления: 2014-11-16