Основные физические величины и законы. Первый постулат Бора (постулат стационарных состояний)

Первый постулат Бора (постулат стационарных состояний)

, ,

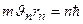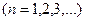где – масса электрона; – скорость электрона на n-й орбите радиусом ; .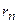

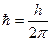Второй постулат Бора

,

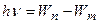где – энергия фотона, излученного (поглощенного) при переходе электрона из стационарного состояния с энергией 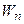в стационарное состояние с энергией .

Энергия электрона на n-й стационарной орбите для ионизованного атома (лишь один электрон на оболочке)

,

где 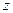– порядковый номер элемента в таблице Менделеева.

Соответственно, для атома водорода

.

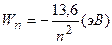Длины волн , излучаемых атомом водорода при переходе электрона с n-й орбиты на m-ю, определяются (как это и следует из второго постулата Бора) обобщенный сериальной формулой

,

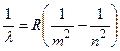где 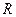– постоянная Ридберга; – определяет спектральную серию (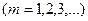; 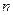– определяет отдельные линии соответствующей серии ;

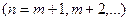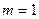– серия Лаймана (ультрафиолетовая область),

– серия Бальмера (видимый свет),

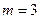– серия Пашена (инфракрасная область),

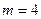– серия Брэкета (инфракрасная область),

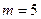– серия Пфунда (инфракрасная область),

– серия Хэмфри (инфракрасная область).

Длина волны 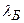(длина волны де Бройля), связанная с движением частицы, обладающей импульсом , выражается формулой

.

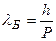В классическом приближении ()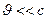

,

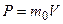где 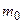– масса покоя частицы.

В релятивистском случае ()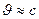

.

Импульс частицы удобно выражать через ее кинетическую энергию :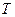

- в классическом случае ;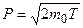

- в релятивистском случае ,

где 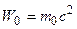– энергия покоя частицы.

Нейтральный атом и его ядро обозначаются одним и тем же символом

,

где – обозначение элемента, 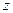– порядковый номер (число протонов в ядре, равное числу электронов в электронной оболочке нейтрального атома), 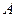– массовое число (число нуклонов-протонов и нейтронов – в ядре, равное округленной до ближайшего целого числа массе атома, выраженной в а.е.м.).

Дефект массы атомного ядра есть разность между суммой масс свободных протонов и нейтронов и массой образовавшегося ядра

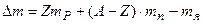
или

,

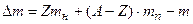где 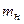– масса атома водорода, – масса рассматриваемого атома.

Энергия связи ядра определяется по общей формуле

.

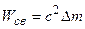Удельная энергия связи .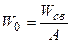

Энергия ядерной реакции

,

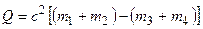где и 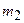– массы покоя ядра мишени и бомбардирующей частицы; 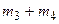– сумма масс покоя ядер продуктов реакции.

Если , то энергия освобождается, реакция экзотермическая. Если 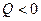, то энергия поглощается, реакция эндотермическая.

Правила смещения:

- для 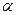– распада ;

- для 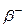– распада ;

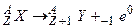- для – распада .

Закон радиоактивного распада

,

где 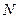– число нераспавшихся ядер в момент времени ; – начальное число нераспавшихся ядер (при 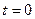); – постоянная радиоактивного распада.

Период полураспада 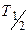– время, за которое число нераспавшихся ядер уменьшается в два раза, связан с постоянной распада

.

Среднее время жизни радиоактивного изотопа – время, за которое число нераспавшихся атомов уменьшается в 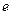раз

.

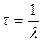Активность изотопа измеряется числом ядер, распавшихся в единицу времени

.

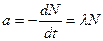Число атомов 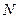, содержащихся в образце изотопа

,

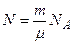где – масса образца; – молярная масса изотопа; 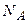– число Авокадро.

Активность образца в начальный момент ()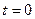

.

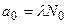Активность образца изменяется со временем по закону

.

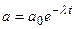Пример 1. Найти радиус, скорость, кинетическую, потенциальную и полную энергию электрона на пятой стационарной орбите в атоме водорода.

Дано: ; ; ; ;

.

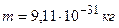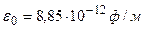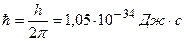Найти: .

Решение. Второй закон Ньютона 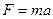для электрона, движущихся по n-й орбите радиуса 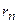под действием кулоновской силы 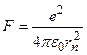со скоростью 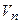и нормальным ускорением принимает вид

или

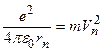. (1.1)

Согласно постулату Бора, момент импульса электрона, движущегося по n-й орбите

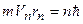
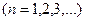. (1.2)

Из системы двух уравнений (1.1) и (1.2) находим

,

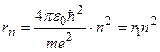где .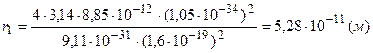

Соответственно, радиус пятой орбиты электрона

.

,

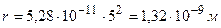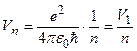где .

Соответственно, скорость электрона на пятой орбите

.

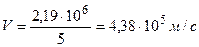Кинетическая энергия электрона на n – й орбите

,

где .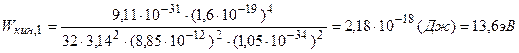

.

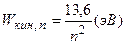Кинетическая энергия электрона на пятой орбите

.

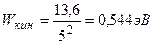Потенциальная энергия взаимодействия электрона (заряд ) и ядра атома водорода – протоном (заряд 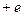) на n-й орбите

.

Потенциальная энергия электрона на пятой орбите

.

Полная энергия электрона на n-й орбите

.

.

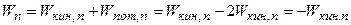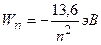Полная энергия электрона на пятой орбите

.

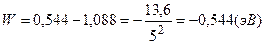Пример 2. Определить длину волны де Бройля 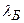электрона, прошедшего ускоряющую разность потенциалов 700 кВ.

Дано: ; ; ; ;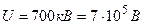

.

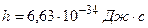Найти: .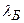

Решение. Связь длины волны де Бройля частицы с ее импульсом

.

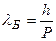В классическом приближении ()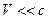

.

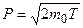В релятивистском случае

,

где 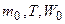– соответственно масса покоя, кинетическая энергия, энергия покоя частицы.

Кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов , определяется работой электрического поля и равна

,

,

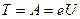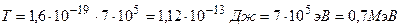а энергия покоя электрона

.

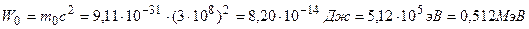Итак, в данном случае (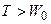) имеем дело с релятивистской частицей.

Тогда искомая длина волны де Бройля

,

.

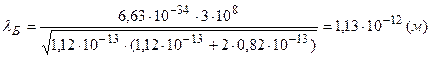Пример 3. В результате соударения дейтрона с ядром бериллия 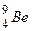образовались новое ядро и нейтрон. Определить порядковый номер и массовое число образовавшегося ядра, записать ядерную реакцию и определить ее энергетический эффект.

Дано: .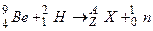

Найти: .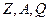

Решение. Из законов сохранения электрического заряда и массовых чисел следует, что 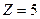, а 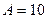, то есть образовавшееся в результате ядерной реакции ядро – изотоп бора . Поэтому ядерную реакцию можно записать в виде

.

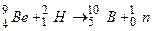Энергетический эффект ядерной реакции

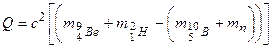, (1.1)

где в первых круглых скобках указаны массы исходных ядер, во вторых – массы ядер продуктов реакции. При расчетах вместо масс ядер используют массы нейтральных атомов, так как, согласно закону сохранения зарядовых чисел, в ядерной реакции (а зарядное число 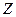нейтрального атома равно числу электронов в его оболочке) получаются одинаковые результаты.

Массы нейтральных атомов в выражении (1.1)

, , ,

.

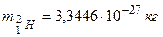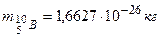Вычисляя, получим

.

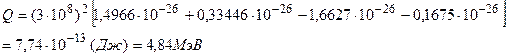Энергетический эффект положителен, реакция экзотермическая.

Пример 4. Первоначальная масса радиоактивного изотопа радона 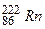(период полураспада (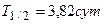) равна . Определить: 1) начальную активность изотопа; 2) его активность через 5 сут.

Дано: , , ,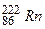

.

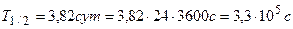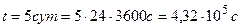Найти: .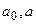

Решение. Начальная активность изотопа

,

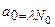где – постоянная радиоактивного распада; – число ядер изотопа в начальный момент времени: 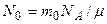, где – молярная масса радона (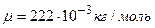); 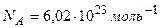– постоянная Авогадро. Учитывая эти выражения, найдем искомую начальную активность изотопа

.

Активность изотопа 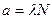, где, согласно закону радиоактивного распада, – число нераспавшихся ядер в момент времени . Учитывая, что 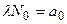найдем, что активность нуклида уменьшается со временем по закону

.

Вычисляя, получим

.

.

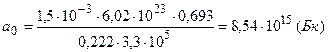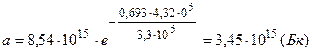Дата добавления: 2014-11-16