Основные физические величины и законы 2 страница

По определению же этой величины имеем

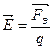или .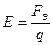

Значит

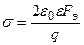, (1.1)

где 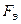– сила, действующая на заряд со стороны электрического поля заряженной плоскости.

Запишем условие равновесия заряженного шарика

.

Введем силу .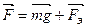

Очевидно, что силы и должны быть направлены вдоль одной прямой, чтобы выполнялось

.

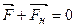В скалярном виде

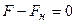. (1.2)

Как видно из рисунка

.

Тогда уравнение (1.2) приобретает вид

.

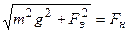Отсюда

. (1.3)

Учитывая, что 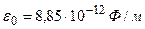, (воздух) и 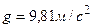, вычисляем :

.

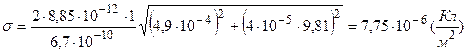Пример 2. Электрон, пройдя в плоском конденсаторе путь от одной пластины до другой, приобрел скорость 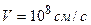. Расстояние между пластинами 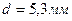. Найти: 1) разность потенциалов между пластинами;

2) поверхностную плотность заряда на пластинах.

Дано: ; .

Найти: , .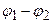

Решение.

1). По определению

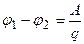, (2.1)

где 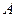– работа электрического поля по перемещению заряда между точками поля с потенциалам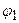и и 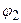. В нашем случае 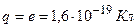– численное значение заряда электрона.

Работа 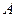электрического поля идет на изменение кинетической энергии электрона

,

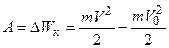где 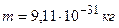– масса электрона, 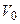и – начальная и конечная скорости электрона.

Как видно из условия, и получаем

.

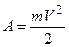Таким образом уравнение (2.1) приобретает вид

.

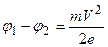Подставим численные значения величин

.

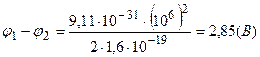2). Поверхностная плотность заряда на пластинах конденсатора определяет напряженность возникающего однородного электрического поля

.

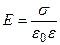Отсюда 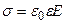. (2.2)

С другой стороны, напряженность однородного поля связана с разностью потенциалов 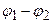точек поля, отстоящих на расстоянии 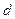одна от другой

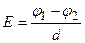. (2.3)

В нашем случае 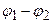разность потенциалов между пластинами конденсатора, 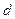– расстояние между пластинами.

Таким образом, уравнение (2.2) с учетом формулы (2.3) принимает вид

.

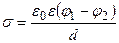Подставим численные значения

.

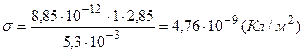Пример 3. К воздушному конденсатору, заряженному до разности потенциалов 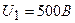и отключенному от источника напряжения, присоединен параллельно второй конденсатор таких же размеров и формы, но с другим диэлектриком (стекло). Определить диэлектрическую проницаемость εстекла, если после присоединения второго конденсатора разность потенциалов уменьшилась до .

Дано: ; ; .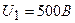

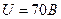Найти: .

Решение. Емкость плоского конденсатора определяется формулой

.

В нашем случае ; .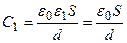

Отсюда следует

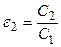. (3.1)

С другой стороны, из определения емкости конденсатора следует:

· для начального состояния первого конденсатора

· для конечных состояний первого и второго конденсаторов

; ,

где – начальный заряд первого конденсатора, 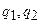– заряды конденсаторов после их параллельного соединения.

Из этих уравнений следует

; ; .

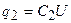По закону сохранения зарядов имеем 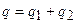, так как конденсаторы отключены от источника напряжения.

То есть .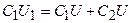

Отсюда

. (3.2)

Подставляя формулу (3.2) в уравнение (3.1), окончательно получаем

; .

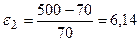Пример 4. Э. д. с. батареи 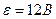. Наибольшая сила тока, которую может дать батарея, 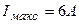. Определить максимальную мощность 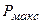, которая может выделяться во внешней цепи.

Дано: ; .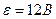

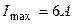Найти: .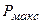

Решение. Мощность, выделяемую во внешней цепи, определяем по формуле

,

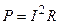где 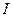– сила тока в цепи, 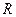– внешнее сопротивление.

По закону Ома для замкнутой цепи

, (4.1)

где 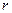– внутреннее сопротивление источника тока.

Учитывая формулу (4.1), получаем

. (4.2)

Для нахождения 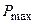вычислим производную 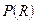и приравняем ее нулю

; .

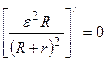Отсюда получаем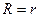

Значит, 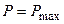, если внешнее сопротивление цепи равно внутреннему.

Тогда формула (4.2) примет вид

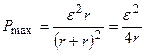. (4.3)

Как видно из формулы (4.1) 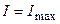при равенстве нулю внешнего сопротивления (ток короткого замыкания)

.

Отсюда находим 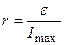. (4.4)

Подставляя формулу (4.4) в уравнение (4.3), окончательно находим

.

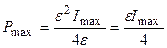С учетом заданных величин получаем

.

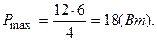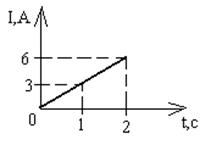Пример 5. Сила тока в проводнике сопротивлением 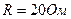нарастает в течение времени 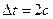по линейному закону от до (рисунок 10). Определить теплоту Q ₁, выделившуюся в этом проводнике за первую и Q ₂ —за вторую секунды, а также найти отношение .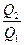

Дано: ;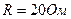

;

;

.

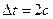Найти: 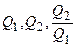. Рисунок 10.

Решение. Закон Джоуля—Ленца в виде справедлив для случая постоянного тока . Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде

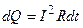. (5.1)

Здесь сила тока I является некоторой функцией времени. В нашем случае 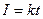, (5.2)

где k — коэффициент пропорциональности, численно равный приращению силы тока в единицу времени, т. е.

.

С учетом (5.2) формула (5.1) примет вид

. (5.3)

Для определения теплоты, выделившейся за конечный промежуток времени Δt, выражение (5.3) надо проинтегрировать в пределах от t₁ до t₂:

.

При определении теплоты, выделившейся за первую секунду, пределы интегрирования 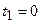, 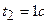и, следовательно,

.

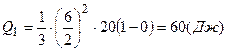При определении теплоты Q ₂ пределы интегрирования 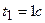, 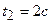и

.

Следовательно, ,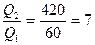

т. е. за вторую секунду выделится теплоты в 7 раз больше, чем за первую.

Пример 6. Три источника тока с ; ; 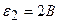и внутренними сопротивлениями, соответственно, 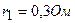; ; 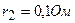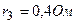, а также сопротивления 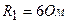; ; 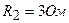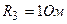соединены как показано на рисунке 11.

Найти токи в каждой ветви цепи и разность потенциалов между точками В и А.

Дано: , , ;

, , ;

, , ;

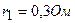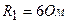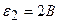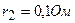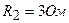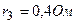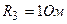Найти: .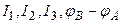

Рисунок 11.

Решение. Воспользуемся правилами Кирхгофа.

Выберем направления токов и укажем на схеме.

В соответствии с первым правилом для узла А имеем

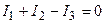. (6.1)

В соответствии со вторым правилом

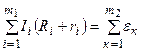
для контура 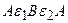(обход по часовой стрелке)

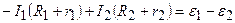; (6.2)

для контура 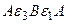(обход против часовой стрелки)

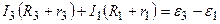. (6.3)

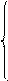Уравнения (6.1), (6.2) и (6.3) после подстановки заданных численных значений величин образуют систему трех уравнений для отыскания токов

.

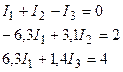Решая эту систему, находим

; ; .

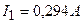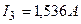Для нахождения разности потенциалов 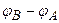воспользуемся законом Ома для неоднородного участка цепи

,

применив его для любой из ветвей данной цепи. Выберем, например, первую ветвь цепи .

Получим .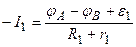

Отсюда .

После подстановки численных значений величин находим

.

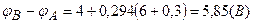Дата добавления: 2014-11-16