
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Физические величины и законы
|
|
|
|
ОСНОВЫ МЕХАНИКИ
представим в виде таблицы
Таблица 1
| Поступательное движение | Вращательное движение | |
| КИНЕМАТИКА Равномерное движение | ||
Путь  , м
Скорость , м
Скорость  , м/с
Ускорение , м/с
Ускорение 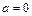 , м/с2 , м/с2
| Угловой путь  , рад
Угловая скорость , рад
Угловая скорость 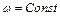 , рад/с
Угловое ускорение , рад/с
Угловое ускорение 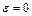 , рад/с2 , рад/с2
| |
| Равнопеременное движение | ||



| 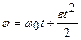
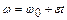
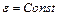
| |
| Произвольное движение | ||
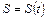
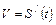 Тангенциальное ускорение
Тангенциальное ускорение  Нормальное ускорение
Нормальное ускорение 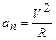
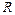 – радиус кривизны траектории
Полное ускорение – радиус кривизны траектории
Полное ускорение 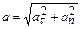
| 


| 


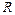 – радиус окружности – радиус окружности
|
| ДИНАМИКА Основные величины | ||
Масса тела  , кг
Сила , кг
Сила  , н
Сила тяжести , н
Сила тяжести  Ускорение свободного
падения
Ускорение свободного
падения  , м/с2
Сила упругости , м/с2
Сила упругости  , ,
 – коэффициент жесткости – коэффициент жесткости
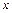 – величина деформации
Сила трения – величина деформации
Сила трения  , ,
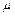 – коэффициент трения – коэффициент трения
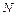 – сила реакции опоры – сила реакции опоры
| Момент инерции  , кг·м2
Для некоторых тел относительно оси симметрии
Тонкий стержень длины , кг·м2
Для некоторых тел относительно оси симметрии
Тонкий стержень длины 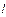  Сплошной диск (цилиндр)
Сплошной диск (цилиндр)  Шар
Шар  Момент силы
Момент силы  , н·м , н·м
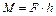 , ,
 – плечо силы – расстояние от оси до линии действия силы – плечо силы – расстояние от оси до линии действия силы 
|
Продолжение таблицы 1
Импульс тела 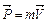 , ,  Работа силы
Работа силы 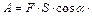 , Дж
Работа переменной силы , Дж
Работа переменной силы 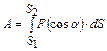 Кинетическая энергия тела
Кинетическая энергия тела 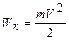 Потенциальная энергия тела:
1). в поле тяжести:
а).
Потенциальная энергия тела:
1). в поле тяжести:
а).   б).
б).  – любое – любое 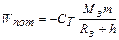 , ,
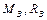 – масса и радиус Земли – масса и радиус Земли
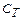 – гравитационная постоянная
2). в поле упругих сил – гравитационная постоянная
2). в поле упругих сил 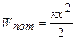
| Момент импульса 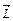 Для вращающегося тела
Для вращающегося тела  , ,  Работа момента силы
Работа момента силы 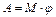 , Дж , Дж
 Кинетическая энергия вращающегося тела
Кинетическая энергия вращающегося тела

|
| Законы | |
Второй закон Ньютона 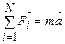 Закон сохранения импульса
Закон сохранения импульса 
| Основной закон динамики вращательного движения 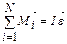 Закон сохранения момента импульса
Закон сохранения момента импульса 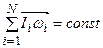
|
Закон сохранения энергии в механике
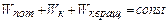
| |
| ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ | |
Уравнение гармонических колебаний 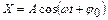 Вид силы, вызывающий гармонические колебания
Вид силы, вызывающий гармонические колебания
 ; ; 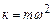 Полная энергия колеблющейся материальной точки массы
Полная энергия колеблющейся материальной точки массы 
 ; ;  ,
где ,
где 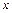 – смещение; – смещение; 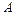 – амплитуда колебания ( – амплитуда колебания (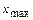 ); );
 – фаза колебания; – фаза колебания;  – начальная фаза; – начальная фаза;
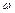 – циклическая частота; – циклическая частота; 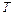 – период колебаний; – период колебаний;  – частота.
Период колебаний физического маятника – частота.
Период колебаний физического маятника
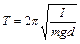 ,
где ,
где  – момент инерции маятника относительно оси колебаний; – момент инерции маятника относительно оси колебаний;
 – расстояние от оси колебаний до центра тяжести; – расстояние от оси колебаний до центра тяжести;
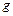 – ускорение свободного падения; – ускорение свободного падения;  – масса маятника. – масса маятника.
|
Пример1. Колесо вращается с постоянным угловым ускорением
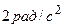
 . Через
. Через  после начала движения полное ускорение точек обода колеса
после начала движения полное ускорение точек обода колеса  . Найти радиус колеса.
. Найти радиус колеса.
Дано:  ;
;  ;
;
 ;
;
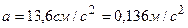 .
.
Найти: 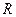 .
.
Рисунок 1.
Решение. Полное ускорение точек обода  .
.
Отсюда 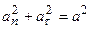 . (1.1)
. (1.1)
Нормальное ускорение 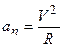 .
.
Так как движение равнопеременное ( ,
, 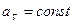 ),
),
то  .
.
В нашем случае  и
и  .
.
Таким образом  .
.
Тангенциальное ускорение связано с угловым
 . (1.2)
. (1.2)
Тогда  . (1.3)
. (1.3)
Подставим формулы (1.2) и (1.3) в формулу (1.1):
 .
.
Отсюда  .
.
Подставляя заданные численные значения величин, получим
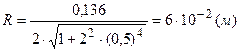 .
.
Пример 2. Молот массой  ударяет по небольшому куску мягкого железа, лежащему на наковальне. Масса наковальни
ударяет по небольшому куску мягкого железа, лежащему на наковальне. Масса наковальни  . Определить
. Определить
к. п. д. удара молота при данных условиях. Удар считать неупругим. Полезной в данном случае является энергия, пошедшая на деформацию куска железа.
Дано:  ;
; 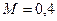 т
т  .
.
Найти:  .
.
Решение. По определению
 (2.1)
(2.1)
В нашем случае затраченная работа равна кинетической энергии молота перед ударом
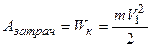 , (2.2)
, (2.2)
где 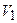 – скорость молота непосредственно перед ударом по железу.
– скорость молота непосредственно перед ударом по железу.
Полезная же работа по закону сохранения энергии равна разности между кинетической энергией молота до удара и кинетической энергией системы – молот + наковальня – после удара.
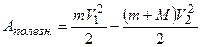 . (2.3)
. (2.3)
Массой небольшого куска железа пренебрегаем. Для определения скорости 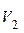 молота и наковальни после удара воспользуемся законом сохранения импульса.
молота и наковальни после удара воспользуемся законом сохранения импульса.
В нашем случае имеем
 .
.
В скалярном виде
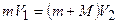 .
.
Отсюда 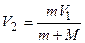 .
.
Подставляя это выражение в формулу (2.3), получим
 . (2.4)
. (2.4)
Подставим формулы (2.4) и (2.2) в исходную формулу (2.1)
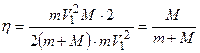 .
.
Подставим численное значение величин
 ;
; 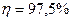 .
.
Пример 3. Через неподвижный блок массой 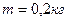 перекинут шнур, к концам которого подвешены грузы массами
перекинут шнур, к концам которого подвешены грузы массами  и
и  .
.
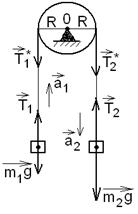 Определить силы натяжения шнура
Определить силы натяжения шнура 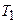 и
и 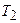 по обе стороны блока во время движения грузов, если массу блока можно считать равномерно распределенной по ободу.
по обе стороны блока во время движения грузов, если массу блока можно считать равномерно распределенной по ободу.
Дано: 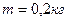 ;
;  ;
;  .
.
Найти: 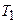 ,
, 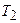 .
.
Решение. Два тела  и
и 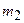 движутся поступательно. Воспользуемся вторым законом Ньютона
движутся поступательно. Воспользуемся вторым законом Ньютона
 .
.
Для первого тела имеем
 . Рисунок 2.
. Рисунок 2.
В скалярном виде (выбираем положительным направление движения вверх)
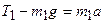 . (3.1)
. (3.1)
Для второго тела
 .
.
Выбираем положительным направление движения вниз
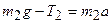 . (3.2)
. (3.2)
Мы учли, что  .
.
Третье тело – блок – вращается.
Воспользуемся основным законом динамики вращательного движения
 .
.
В нашем случае
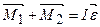 .
.
Считая положительным направление вращения по часовой стрелке, получаем
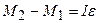 .
.
Учитывая, что
 ;
;  ;
;  ;
; 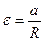 ,
,
получаем  ,
,
то есть 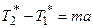 .
.
Согласно третьему закону Ньютона с учетом невесомости шнура
 и
и 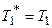 .
.
Таким образом
 (3.3)
(3.3)
 Итак, получили систему трех уравнений с тремя неизвестными:
Итак, получили систему трех уравнений с тремя неизвестными: 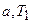 и
и 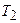 .
.
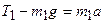 ,
,
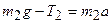 ,
,
 .
.
Сложив, соответственно, левые и правые стороны уравнений, находим
 .
.
Отсюда
 . (3.4)
. (3.4)
Подставляя формулу (3.4) в первое уравнение системы, находим
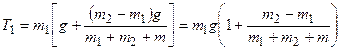 .
.
После подстановки численных значений
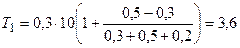 (н).
(н).
Соответственно, второе уравнение системы с учетом формулы (3.4) примет вид
 .
.
 (н).
(н).
Пример 4. На краю горизонтальной платформы, имеющей форму диска радиусом  , стоит человек. Масса платформы
, стоит человек. Масса платформы  , масса человека
, масса человека  . Платформа может вращаться вокруг вертикальной оси, проходящей через ее центр. Пренебрегая трением, найти, с какой угловой скоростью будет вращаться платформа, если человек будет идти вдоль ее края со скоростью
. Платформа может вращаться вокруг вертикальной оси, проходящей через ее центр. Пренебрегая трением, найти, с какой угловой скоростью будет вращаться платформа, если человек будет идти вдоль ее края со скоростью
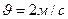
 относительно платформы.
относительно платформы.
Дано:  ;
;
 ;
;
 ;
;
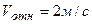 .
.
Найти: 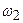 .
.
Рисунок 3.
Решение. Воспользуемся законом сохранения момента импульса
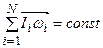 .
.
В нашем случае  ,
,
так как в начале ни человек, ни платформа не двигались.
В скалярном виде, считая положительным направление движения человека, получим
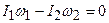 . (4.1)
. (4.1)
Моменты инерции человека 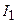 и платформы
и платформы 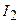 относительно оси вращения, соответственно, равны
относительно оси вращения, соответственно, равны
 ;
;  . (4.2)
. (4.2)
Угловая скорость  человека относительно Земли есть
человека относительно Земли есть
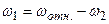
и так как  ,
,
то  . (4.3)
. (4.3)
Подставим формулы (4.3) и (4.2) в формулу (4.1)
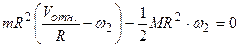 .
.
Отсюда  .
.
Подставляем численные значения
 .
.
Пример 5. Вагон массой  движется на упор со скоростью
движется на упор со скоростью
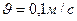 . При полном торможении вагона буферные пружины сжимаются на
. При полном торможении вагона буферные пружины сжимаются на  . Определить максимальную силу
. Определить максимальную силу 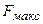 сжатия буферных пружин и продолжительность
сжатия буферных пружин и продолжительность  торможения.
торможения.
Дано:  т
т  ;
;
 ;
; 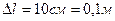 .
.
Найти:  и
и  .
.
Решение. При сжатии пружин сила сжатия определяется их силой упругости 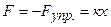 ,
,
где 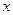 – величина сжатия;
– величина сжатия; 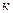 – коэффициент жесткости пружин.
– коэффициент жесткости пружин.
Соответственно, искомая сила максимального сжатия
 . (5.1)
. (5.1)
По закону сохранения энергии кинетическая энергия вагона при остановке перейдет в потенциальную энергию сжатия пружин
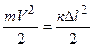 .
.
Отсюда  .
.
Подставляя выражение для «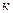 » в формулу (5.1), получим
» в формулу (5.1), получим
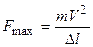 .
.
Вычисляем 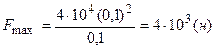 .
.
Для нахождения времени сжатия пружин используем то, что под действием сил упругости смещение 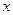 вагона определяется гармоническим законом
вагона определяется гармоническим законом
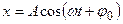 ,
,
а скорость вагона соответственно
 .
.
 В начальный момент сжатия
В начальный момент сжатия  было
было
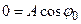 ,
,
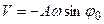 .
.
Отсюда
 ;
; 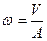 . (5.3)
. (5.3)
При остановке через  имеем
имеем
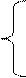
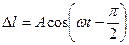 ,
,
 .
.
Отсюда
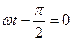 . (5.4)
. (5.4)
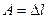 . (5.5)
. (5.5)
Подставляя в формулу (5.4) выражение (5.3) с учетом формулы (5.5) получим 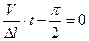 .
.
Окончательно  .
.
 .
.
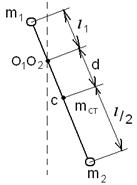
Пример 6. На концах стержня массой 1 кг и длиной 40 см укреплены одинаковые грузы массами 400 г по одному на каждом конце. Стержень с грузами колеблется около оси, проходящей через точку, удаленную на 10 см от одного из концов стержня. Определить период колебаний стержня.
 Дано:
Дано:  ;
;
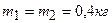 ;
;
 ;
;
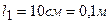 .
.
Найти: 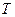 .
.
Рисунок 4.
Решение. Период колебаний физического маятника (а это – любое тело, колеблющееся около оси, не проходящей через центр тяжести) определяется формулой
 , (6.1)
, (6.1)
где 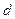 – расстояние от оси колебаний до центра тяжести маятника. В нашем случае
– расстояние от оси колебаний до центра тяжести маятника. В нашем случае
 . (6.2)
. (6.2)
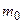 – общая масса маятника.
– общая масса маятника.
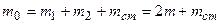 . (6.3)
. (6.3)
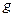 – ускорение свободного падения.
– ускорение свободного падения.
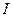 – момент инерции маятника относительно оси колебаний
– момент инерции маятника относительно оси колебаний
 . (6.4)
. (6.4)
Моменты инерции грузиков, как материальных точек, равны
 ;
;  . (6.5)
. (6.5)
Моменты инерции стержня находим, используя теорему Штейнера-Гюйгенса  .
.
Момент инерции  стержня относительно оси, проходящей через центр тяжести, равен
стержня относительно оси, проходящей через центр тяжести, равен 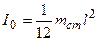 и, значит,
и, значит,
 . (6.6)
. (6.6)
Подставляя формулы (6.5) и (6.6) в выражение (6.4) находим
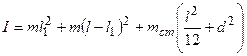 .
.
И, подставляя это выражение вместе с формулой (6.3) в выражение (6.1), окончательно получаем
 .
.
Вычисляем 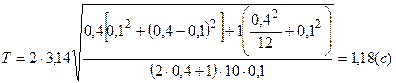 .
.
 .
.
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 595; Нарушение авторских прав?; Мы поможем в написании вашей работы!