Основные физические величины и законы. Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона) ,

Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона) ,

где – давление газа (); – объем занимаемый газом ();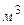

– количество молей газа; 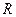– универсальная постоянная, ;

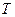– абсолютная температура газа, .

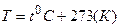Для однородного газа

,

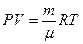где – масса газа (кг); – масса моля (молярная масса)газа ().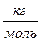

Для смеси газов

.

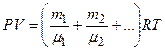Парциальное давление 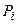«i» компоненты смеси газов находят из

.

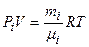Основное уравнение молекулярно-кинетической теории идеальных газов

,

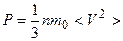где 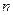– концентрация молекул, 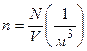; 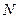– общее число молекул газа; 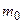– масса одной молекулы (кг); 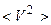– средний квадрат скоростей молекул (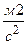); – объем, занимаемый газом ().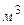

Средняя кинетическая энергия молекулы

,

где 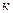– постоянная Больцмана, ; 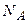– число Авогадро (число молекул в одном моле); 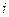– число степеней свободы молекул. Одноатомный газ 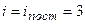, двухатомные молекулы , многоатомные молекулы .

Средняя скорость молекул

.

Средняя квадратичная скорость молекул

.

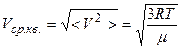Средняя длина свободного пробега молекул

,

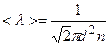где 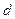– эффективный диаметр молекулы.

Внутренняя энергия идеального газа

.

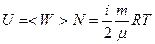Работа, совершаемая газом при изменении объема от 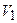до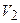

.

Работа газа в изопроцессах:

изохорный (), ;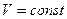

изобарный (), ;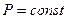

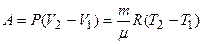изотермический , .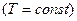

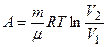Теплота, полученная (отданная) газом

,

где 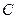– удельная теплоемкость ().

Первое начало термодинамики

,

где – изменение внутренней энергии.

Удельная теплоемкость газа при постоянном объеме

.

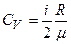Удельная теплоемкость газа при постоянном давлении

.

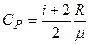Уравнение адиабатического (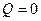) процесса – уравнение Пуассона

,

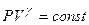где – показатель адиабаты.

Работа газа при адиабатическом процессе

;

.

Коэффициент полезного действия тепловой машины

,

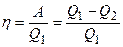где – количество теплоты, полученное системой за один цикл; 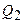– количество теплоты, отданное системой за один цикл; 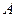– работа, совершаемая за один цикл.

Коэффициент полезного действия цикла Карно (идеальной тепловой машины) ,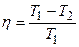

где 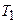– температура нагревателя; 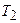– температура охладителя.

Пример 1. Один баллон емкостью 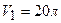содержит азот под давлением , другой баллон емкостью 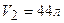содержит кислород под давлением 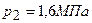. Оба баллона были соединены между собой и оба газа смешались, образовав однородную смесь (без изменения температуры). Найти парциальные давления и обоих газов в смеси и полное давление 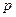смеси.

Дано: ;

;

;

;

.

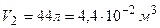Найти: , , .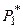

Решение. Парциальное давление азота 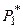и кислорода находим из уравнений

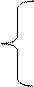
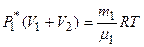
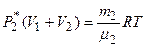. (1.1)

В начальных состояниях уравнения Менделеева-Клапейрона для азота и кислорода есть

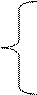
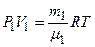
. (1.2)

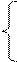Учитывая формулы (1.2), уравнения (1.1) принимают вид

.

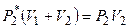Получаем

; .

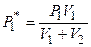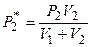Подставим заданные численные значения

,

.

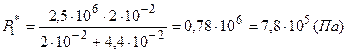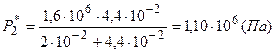Полное давление смеси газов равно сумме парциальных

;

.

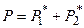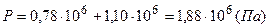Пример 2. Определить среднюю кинетическую энергию вращательного движения одной молекулы двухатомного газа, если суммарная кинетическая энергия молекул одного киломоля этого газа .

Дано: ;

.

Найти: .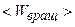

Решение. Средняя кинетическая энергия вращательного движения молекулы

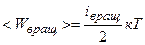. (2.1)

где 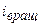– число степеней свободы вращательного движения молекулы.

Суммарная кинетическая энергия всех молекул газа (внутренняя энергия идеального газа)

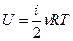, (2.2)

где 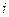– общее число степеней свободы молекулы (поступательного и вращательного движений).

Отсюда 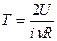. (2.3)

Подставляя формулу (2.3) в уравнение (2.1), получим

.

Учитывая, что ,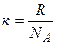

где 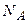– число Авокадро, 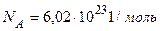, окончательно получаем

.

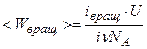Подставим численные значения величин, учитывая, что для двухатомного газа

; .

.

Пример 3. Определить среднюю длину свободного пробега < > и среднее число столкновений 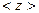молекулы гелия за 1с при температуре

и давлении .

Дано: ; ;

;

.

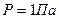Найти: , .

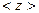Решение. Средняя длина свободного пробега молекул определяется формулой

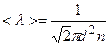, (3.1)

где 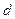– эффективный диаметр молекулы. Гелий – газ одноатомный. Диаметр гелия находим из справочных таблиц. 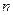– число атомов в единице объема.

Из уравнения Менделеева-Клапейрона в виде 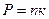T находим

, (3.2)

где 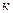– постоянная Больцмана, .

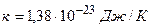Перепишем уравнение (3.1) с учетом формулы (3.2)

.

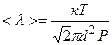Подставим численные значения

.

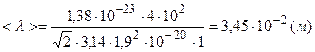Среднее число столкновений атомов за единицу времени можно найти из формулы

.

Средняя скорость – атомов определяется формулой

.

Таким образом

.

Подставим численные значения

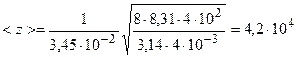(1/с).

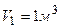Пример 4. Кислород массой занимает объем и находится под давлением 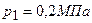. При нагревании газ расширился при постоянном давлении до объема , а затем его давление возросло до 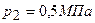при неизменном объеме. Найти изменение внутренней энергии газа, совершенную им работу А и теплоту Q, переданную газу. Построить график процесса.

Дано: ; ;

; ;

;

.

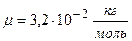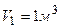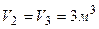Найти: , , .

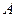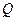Решение. Изменение внутренней энергии газа выражается формулой

.

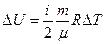В данном случае .

, (4.1)

где i – число степеней свободы молекул газа (для двухатомных молекул кислорода i = 5).

Температуры газа в каждом состоянии найдем, используя уравнение Менделеева - Клапейрона

.

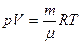Отсюда .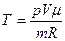

Подставим численные значения параметров каждого из трех состояний

;

.

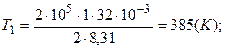
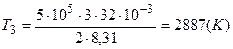Подставляя в выражение (4.1) числовые значения находим

.

Работа расширения газа при постоянном давлении выражается формулой

.

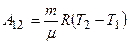Работа газа при 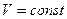равна нулю.

.

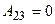Таким образом, полная работа, совершаемая газом, равна

.

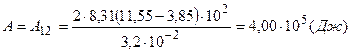Согласно первому началу термодинамики теплота Q, переданная газу, равна сумме изменения внутренней энергии и работы А: , следовательно,

.

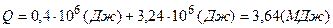График процесса приведен на рисунке 5.

Рисунок 5.

Пример 5. Идеальная тепловая машина работает по циклу Карно. Температура нагревателя в 2 раза выше температуры охладителя. Работа цикла

1 кДж. Какое количество теплоты передано охладителя за один цикл?

Дано: ;

.

Найти: .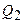

Решение. Количество теплоты, отданное охладителю, равно разности между теплотой, полученной газом от нагревателя и совершенной им работой

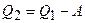. (5.1)

Из определения К.П.Д. тепловой машины

следует .

Теперь уравнение (5.1) примет вид

. (5.2)

Для идеальной тепловой машины К.П.Д. равно

.

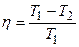По условию задачи .

Значит . (5.3)

Подставляя формулу (5.3) в уравнение (5.2), и с учетом численного значения 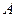, получаем

.

Дата добавления: 2014-11-16