Согласно закону радиоактивного распада

Тогда

Решение. Пусть яма расположена в интервале (0, L) оси х, вероятность обнаружить частицу в интервале (L/3, 2L/3).

Подставляя в соотношение неопределенностей, получаем

откуда

Неопределенность импульса не должна превышать значения самого импульса, т.е.

,

где E_к - кинетическая энергия электрона (E_к ≈ 10 эВ «E_o = 0,511 МэВ). Заменяя ΔP_x максимальным его значением – импульсом электрона, получаем:

(м)

Пример 4. Электрон размещается в одномерной, бесконечно глубокой потенциальной яме шириной l. Найти вероятность того, что электрон в возбужденном состоянии с n =2 будет находиться в средней трети ямы.

Для частицы в возбужденном состоянии n=2 волновая функция определена формулой (рис. 2.2):

Подставляя ее в формулу для w получаем:

Для интегрирования произведем замену:

Пример 5. Найти энергию связи и удельную энергию связи ядра атома бериллия

Решение. Энергию связи ядра найдем из выражения:

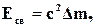
где - дефект массы

где m_p, m_n и - массы протона, нейтрона и ядра соответственно. Так как в таблице 2.3 приложения даны массы не ядер, а нейтральных атомов учтем это:

где m_e – масса электрона, тогда выражение для дефекта будет выглядеть следующим образом:

или

Энергию связи ядра найдем, умножив дефект массы на с²=931,5 МэВ/а.е.м.

Воспользовавшись таблицами 2.3 и 2.4 приложения, получим:

Е_св= 931,5[4(1,00728+0,00055)+6 ּ 1,00867-10,01354]=65 (МэВ)

Удельную энергию связи, т.е. энергию связи приходящуюся на один нуклон, найдем, разделив Е_св на общее число нуклонов:

Е_{св уд} =

Пример 6. При измерении периода полураспада счетчик в течении 1 мин насчитал 250 импульсов, а спустя 1 час после начала первого измерения- 92 импульса в минуту. Найти постоянную распада λ и период полураспада Т.

Решение. Число импульсов Δn регистрируемых счетчиком за время Δt, пропорционально числу распадов ΔN. При первом измерении

(1)

где N₁ -количество нераспавшихся радиоактивных ядер к моменту начала первого счета; k -коэффициент пропорциональности.

При втором измерении

, (2)

где N₂ -количество нераспавшихся ядер к началу второго измерения; Δt₂= Δt₁=1 мин

времена измерений.

и , (3)

где 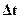-время, прошедшее от первого до второго измерения (по условию =60 мин),

Разделим уравнение (2) на уравнение (1) и, учитывая (3), получим:

или

После логарифмирования получим:

Итак, постоянная распада

,

период полураспада:

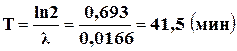
Пример 7. Радиоактивное ядро магния 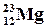выбросило позитрон и нейтрино. Найти энергию β⁺ -распада ядра.

Решение. Реакцию β⁺- распада можно записать так:

,

здесь - позитрон, а 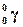-нейтрино.

Энергетический эффект ядерной реакции подсчитывается по формуле:

Перейдем от масс ядер к массам атомов:

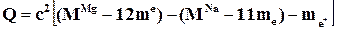
Так как массы электрона и позитрона одинаковы, то

Q=c²(M^Mg-M^Na-2m_e)

Произведя подстановку табличных значений (см. таблицу 2.3 приложения), получаем:

Q=931,5(22,99414-22,98977-0,0011)=3,04(МэВ)

Пример 8. Написать недостающие обозначения ядерной реакции и найти энергию, выделяющуюся в результате этой реакции.

Решение. В развернутом виде эта ядерная реакция записывается:

В силу законов сохранения зарядового и массового числа имеем:

Z=(1+6)-7=0, A=(1+14)-14=1,

т.е. налетающая частица является нейтроном .

Энергия реакции представима формулой:

Q=c²[( +m_n)-(m_p+ )

или, перегруппировывая и заменяя массы ядер на массы атомов, в

Подставляя из таблиц 2.3 и 2.4 значения входящих в эту формулу величин и

учитывая связь атомной единицы массы с энергией (см. 1.6), имеем:

Q=931,5[(14,00307-14,00324)+(1,00867-1,00783)]=0,62 (МэВ).

Пример 9.: Электрон в атоме водорода находится на энергетическом уровне 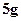. Определить орбитальный момент импульса 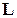этого электрона, а также наименьший угол, который 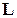может составить с осью . Фотон какой энергии может быть испущен этим электроном спонтанно?

Решение: 1) В -состояниях азимутальное квантовое число 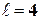Поэтому орбитальный момент импульса электрона

,

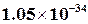
где = - постоянная Планка. При заданной величине момента импульса (при заданном ) его проекция на ось может быть равной

, (1)

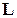где - магнитное квантовое число (). В соответствии с (1), может принимать значение, каждому из которых соответствует определенная ориентация момента импульса относительно оси . При этом, угол между и осью будет минимальным тогда, когда будет максимальной (см. рис.). Согласно (1), максимальное значение проекции момента импульса на ось

Дата добавления: 2014-11-16