Поверхня з ребром звороту

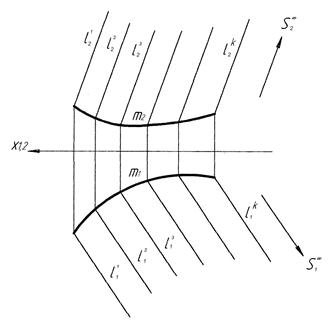
Поверхня з ребром звороту (торс) утворюється переміщенням твірної, яка у всіх своїх положеннях є дотичною до напрямної (просторової кривої лінії). Визначник торсової поверхні: Ф = [(l, m) (" l È m)],

де: l – твірна, пряма лінія,

m – напрямна, крива лінія.

Крива напрямна називається ребром звороту. Приклад поверхні показано на рисунку 6.5.

Рисунок 6.3	Рисунок 6.4

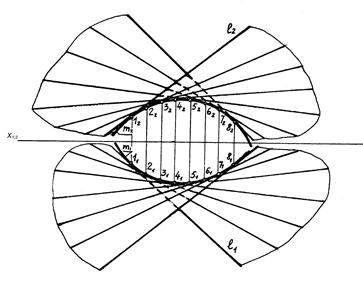
Рисунок 6.5

6.2 Лінійчаті нерозгортні поверхні. Поверхні з двома напрямними лініями

Ця група поверхонь має дві напрямні. Твірна (пряма лінія) безперервно

переміщується по двох напрямних і залишається паралельною до площини,

яка називається площиною паралелізму. Площиною паралелізму може бути проекціювальна площина, або площина рівня, а також площина проекції. Ця група поверхонь називається “Поверхні з площиною паралелізму”. Їх ще називають поверхнями Каталана.

Є три поверхні Каталана:

- коса площина (гіперболічний параболоїд),

- коноїд,

- циліндроїд.

Визначник поверхонь Каталана: Ф = [(l, m, n, S) (" l Ç m, n; " l || S)],

де: l – твірна, пряма лінія;

m, n – напрямні, криві або прямі лінії;

S – площина паралелізму.

6.2.1 Гіперболічний параболоїд

Гіперболічний параболоїдвідноситься до групи поверхонь з площиною паралелізму. У цієї поверхні обидві напрямні m і n мимобіжні прямі лінії (рис. 6.6).

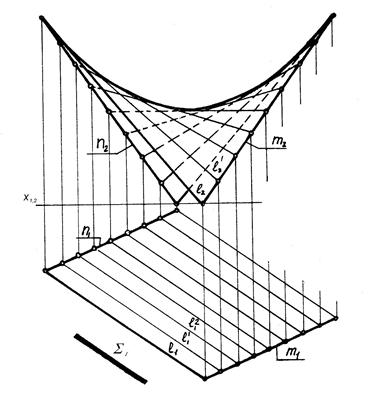
Рисунок 6.6

6.2.2 Коноїд

Коноїд відноситься до групи поверхонь з площиною паралелізму. У коноїда одна напрямна – пряма лінія, друга напрямна – крива лінія (рис.6.7).

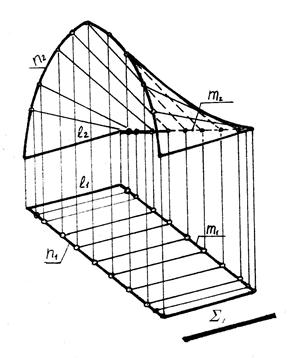
Рисунок 6.7

6.2.3 Циліндроїд

Циліндроїд відноситься до групи поверхонь з площиною паралелізму. У циліндроїда обидві напрямні – криві лінії (рис. 6.8).

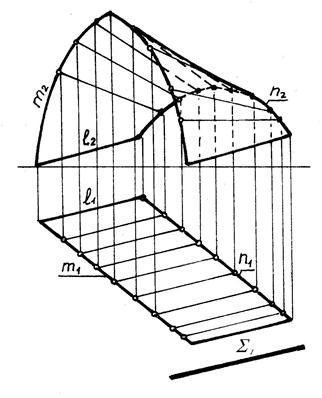
Рисунок 6.8

6.3 Гвинтові поверхні

Гвинтові поверхні утворюються гвинтовим рухом твірної по гвинтовій напрямній лінії. Лінійчаті гвинтові поверхні називаються гелікоїдами.

Визначник гвинтових поверхонь: Ф = [(l, m, n, i) (" l Ç m)]

де: l – твірна, пряма лінія (може бути і крива),

m – напрямна, гвинтова лінія,

n – друга напрямна гвинтова лінія (для відкритих гелікоїдів),

i – нерухома пряма (вісь)

1. Прямий закритий гелікоїд. Утворюється рухом прямої твірної по двох напрямних. Одна напрямна гвинтова лінія, друга – вісь гвинтової лінії. Твірна перетинає вісь гвинтової лінії під прямим кутом.

2. Косий закритий гелікоїд. Утворюється рухом прямої твірної по двох напрямних. Одна напрямна гвинтова лінія, друга – вісь гвинтової лінії. Твірна перетинає вісь гвинтової лінії і має постійний кут нахилу до неї.

3. Прямий відкритий гелікоїд. Твірна пряма лінія з віссю не перетинається і рухається по двох кривих напрямних.

4. Косий відкритий гелікоїд. У цієї поверхні кут між твірною прямою лінією і віссю не дорівнює 90^°.

На рисунку 6.9 наведено приклад гвинтової поверхні – прямий закритий гелікоїд.

Рисунок 6.9

6.4 Криволінійчаті поверхні

У криволінійчатих поверхонь твірна – крива лінія. До таких поверхонь відносяться деякі поверхні обертання.

6.4.1 Поверхні обертання

Поверхні, які утворені обертанням твірної лінії навколо нерухомої осі, називають поверхнями обертання.

Визначник поверхонь обертання: Ф = [(l, i) (l 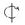i)]

де: l – твірна (пряма або крива лінія)

i – вісь обертання

До поверхонь обертання відносяться:

1. Сфера. Поверхня сфери утворюється при обертанні кола навколо його діаметра.

2. Тор. Поверхня тора утворюється при обертанні твірного кола навколо осі i. Відомі два види тора: а) відкритий – твірне коло не перетинає вісь обертання; б) закритий – твірне коло перетинається з віссю обертання.

3. Еліпсоїд обертання. Поверхня еліпсоїда обертання утворюється при обертанні еліпса навколо його осі.

4. Параболоїд обертання. Поверхня обертання параболоїда утворюється при обертанні параболи навколо її осі.

5. Гіперболоїд обертання. Поверхня обертання гіперболоїда утворюється при обертанні гіперболи навколо її уявної осі.

Кола на поверхні обертання називаються паралелями. Паралель утворюється площиною, яка перетинає поверхню перпендикулярно до осі обертання. Паралель з найменшим радіусом називається горлом. Паралель з найбільшим радіусом називається екватором. Площина, що перетинає поверхню і проходить через вісь обертання утворює лінію, яка називається меридіан. В тому випадку, коли площина проходить через вісь обертання і паралельна площині проекції, утворюється головниймеридіан. На рисунку 6.11 наведено приклад поверхні обертання загального вигляду де побудовані ці лінії.

6.5 Точка і лінія на кривій поверхні

Точка належить поверхні, якщо вона лежить на лінії (прямій або кривій), яка належить цій поверхні. Для того, щоб побудувати точку A на поверхні, вісь обертання якої перпендикулярна до П₁, через фронтальну проекцію точки проводять паралель(рис. 6.10, а). На П₂ ця паралель відображається в пряму лінію перпендикулярну до осі обертання. Потім паралель проекціюють на П₁, де вона зображається у вигляді кола. Радіус паралелі R вимірюють від осі обертання до контура поверхні. Із фронтальної проекції точки А проводять вертикальну лінію зв’язку на горизонтальну проекцію паралелі і отримують проекцію точки А₁ на П₁. На прямолінійчатих поверхнях точки будують за допомогою прямих ліній, що утворюють поверхню. На рисунку 6.10, б показано приклад побудови точки В на поверхні прямого кругового конуса. На рисунку 6.11 наведено приклад побудови кривої лінії на поверхні обертання. Окремі точки А, E, B, N, C, D, що належать поверхні, будують за допомогою паралелей, з’єднують і отримують криву лінію l.

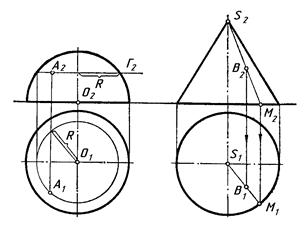
а)	б)
Рисунок 6.10

Рисунок 6.11

6.6 Переріз поверхні площиною

При перерізах поверхонь площиною утворюється плоска крива лінія, кожна точка якої є точкою перетину лінії каркаса поверхні з січною площиною. Для побудови точок перерізу можуть бути застосовані метод допоміжних січних площин та метод перетворення площин проекцій. Звичайно обирають допоміжні січні площини рівня або проекціювальні площини, що дає можливість визначити множину точок перетину ліній каркаса поверхні з допоміжною площиною. Способи перетворення площин проекцій дозволяють перевести площину загального положення в проекціювальне положення і цим спростити розв’язування задачі.

6.6.1 Переріз поверхні проекціювальною площиною

Якщо поверхню перерізає площина окремого положення, то задача побудови лінії перерізу зводиться до пошуку її другої проекції або до визначення другої проекції множини точок, що належать поверхні. Для побудови другої проекції лінії перерізу досить задати поверхню у вигляді простих ліній каркаса, проекції яких можна накреслити інструментально без додаткових побудов. Відсутню проекцію кожної точки перерізу визначають як проекцію точки, що належить відповідній лінії каркаса.

На рисунку 6.12 показано побудову натуральної величини фігури перерізу конуса обертання. Поверхню конуса перетинає фронтально-проекціювальна площина Г.

Рисунок 6.12

Точки горизонтальної і профільної проекції будують як проекції точок, що належать лініям каркаса конуса за допомогою вертикальних і горизонтальних ліній зв’язку. Точки 2, 3, А, B, D, E, K, C з’єднують і на П₁ отримують горизонтальну проекцію еліпса m₁, на П₃ – профільну проекцію m₃. Потім вводять додаткову площину проекції П₄ паралельно січній площині Г (Г₂) і на неї проекціюють отримані точки. На П₄ всі проекції точок з’єднують і отримують натуральну величину фігури перерізу m₄.

На рисунку 6.13 наведено приклад, де криволінійчату поверхню обертання (тор) перетинає горизонтально-проекціювальна площина.

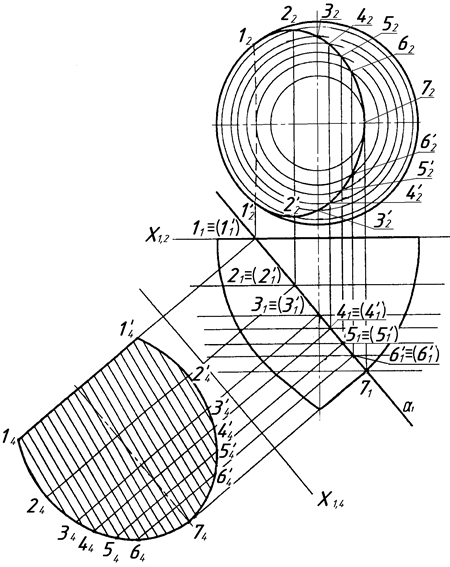
Рисунок 6.13

Для побудови натуральної величини фігури перерізу вводять додаткову площину проекції П₄ паралельно січній площині. На епюрі вісь х_1,4 проведена паралельно горизонтальній проекції січної площини a₁. Точки на кривій лінії фігури перерізу 1 - 7, 1^¢ - 6^¢ визначають там, де січна площина перетинає лінії, що належать поверхні. Такими лініями на поверхні тора є паралелі (кола). Точки, що належать фігурі перерізу, спочатку будують на П₂ за допомогою паралелей. Потім точки за допомогою ліній зв’язку проекціюють на П₄. Координати точок вимірюють на П₂. Це будуть відстані від осі х_1,2 до фронтальних проекцій точок. Ці відстані відкладають на П₄ на лініях зв’язку від нової осі х_1,4. Проекції точок на П₄ з’єднують і отримують натуральну величину фігури перерізу.

6.6.2 Переріз поверхні площиною загального положення

Для побудови лінії перерізу поверхні площиною загального положення необхідно перетворити креслення так, щоб січна площина стала в новому положенні проекціювальною.

Алгоритм побудови фігури перерізу

1. В заданій площині загального положення будують лінію рівня (горизонталь або фронталь). Якщо площина задана слідами, або горизонталлю і фронталлю, що перетинаються, то лінію рівня будувати не треба.

2. Використовують метод заміни площин проекцій. Перпендикулярно до натуральної величини прямої рівня, або сліду площини, проводять нову площину проекції П₄.

3. На П₄ проекціюють задану криву поверхню (або багатогранник) і січну площину, яка перетворюється у пряму лінію (Цю проекцію січної площини називають виродженою).

4. На П₄ позначають точки перетину проекції січної площини з проекціями ліній каркаса поверхні (з твірними та напрямними кривої поверхні або ребрами багатогранника).

5. Отримані точки за допомогою ліній зв'язку проекціюють на П₁ та П₂. Потім точки з'єднують суцільною або штриховою лінією, у залежності від того, видима лінія чи невидима.

6. Паралельно січній площині, яка на П₄ спроекційована у пряму лінію (вироджена), проводять ще одну додаткову площину проекції П₅.

7. На П₅ проекціюють тільки точки лінії перетину, з'єднують ці точки і отримують натуральну величину фігури перерізу.

На рисунку 6.14 наведено приклад побудови натуральної величини фігури перерізу. Поверхню прямого кругового конуса перетинає площина загального положення, яка задана прямими a і b, що перетинаються. В цій площині q (a Ç b) проводять горизонталь h і перпендикулярно до неї вводять додаткову площину проекції П₄. На епюрі нова вісь s_1,4 проведена перпендикулярно до горизонтальної проекції горизонталі h₁. На П₄ січна площина відображається у пряму лінію, тобто займає проекціювальне положення. Точки на кривій лінії фігури перерізу визначають там, де проекція січної площини q₄ перетинає паралелі конуса. За допомогою ліній зв’язку ці точки проекціюють спочатку на П₁ а потім на П₂, з’єднують і отримують горизонтальну і фронтальну проекції фігури перерізу. Для побудови натуральної величини фігури перерізу, вводять ще одну додаткову площину проекції П₅ паралельно проекції січної площини q₄. На П₅ проекціюють точки 2 - 12 і отримують натуральну величину фігури перерізу.

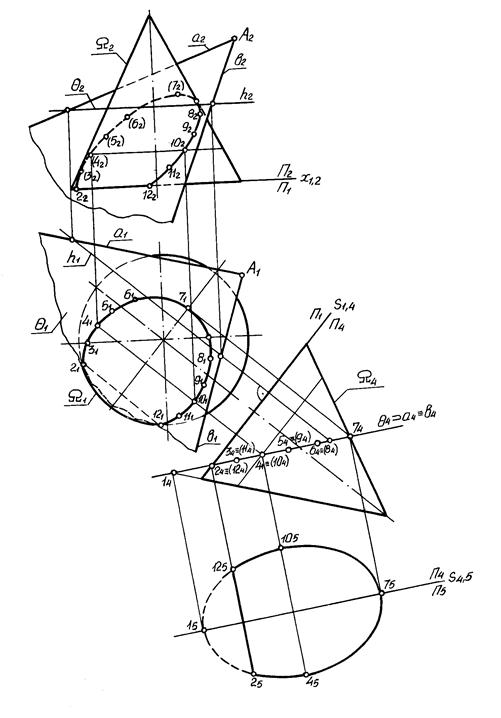
Рисунок 6.14

6.7 Перетин прямої лінії з поверхнею (Проникнення)

Пряма перетинає поверхню другого порядку в двох точках. Винятком є випадок, коли пряма дотична до поверхні і має з нею одну спільну точку. У загальному випадку точки перетину прямої з кривою поверхнею або багатогранником можуть бути визначені за допомогою січної площини, що проводиться через пряму (рис. 6.15).

Алгоритм розв’язання задачі

1. Через дану пряму, яка перетинає поверхню, проводять допоміжну січну площину (площину окремого положення).

2. Будують лінію перетину (фігуру перерізу) поверхні з січною площиною. На кривій поверхні фігура перерізу – це плоска крива лінія другого порядку, на багатограннику – це багатокутник.

3. Знаходять точки перетину прямої з фігурою перерізу.

4. Визначають видимість прямої відносно поверхні.

Рисунок 6.15

Дата добавления: 2014-11-08