Средние величины в статистике

Задачи для самостоятельного решения

Задача № 1.

Урожайность сахарной свеклы в хозяйстве в предыдущем году составила 400 ц/га. Планом за отчётный год предусматривалось собрать 440 ц/га. Фактически собрано 506 ц/га.

Определите относительные величины выполнения плана, планового задания и динамики.

Задача № 2.

Имеются следующие данные о численности детей, родившихся в городе А (чел.):

Мальчики – 40618

Девочки – 35017

Определите относительную величину координации.

Задача № 3.

Имеются следующие данные розничного товарооборота:

Таблица 4.4

Универмаги	Розничный товарооборот (тыс. грн).
Фактический за базисный год	отчётный год
план	фактически
"Крым" "Центральный"		85,6

Определите относительные величины:

1. планового задания;

2. выполнения плана за отчётный период;

3. динамику фактического товарооборота.

Задача № 4.

Планом предусматривалось повысить производительность труда на 4 %, фактически она повысилась на 9,2 %.

Определите степень выполнения плана по росту производительности труда.

Средними величинами в статистике называют такие показатели, которые выражают типичные черты и дают обобщающую количественную характеристику уровня какого-то варьирующего признака по совокупности однородных явлений.

Вычисление средних величин в статистике существенно отличается от их вычисления в математике. Это отличие обусловлено, прежде всего, тем, что средние в математике представляют собой отвлечённые абстрактные величины, которые не отражают качественных признаков каких-либо конкретных явлений.

Статистические же средние величины всегда выражают качественные стороны изучаемых процессов. В этих условиях для каждого случая важно правильно выбрать форму средней величины.

Исходной базой или критерием выбора формы средней является соотношение, которое выражает смысл средней величины и их зависимость от других показателей.

Средние могут вычисляться как для совокупности в целом, так и для отдельных её групп. Первые называются общими средними, а вторые – групповыми или частными средними. Общая средняя может быть вычислена как средняя из групповых средних и взвешенная по объектам групп.

Средние величины могут быть как абсолютными, так и относительными.

Средняя величина должна вычисляться с учётом экономического содержания определяемого показателя. Каждый показатель имеет своё, только ему присущее, содержание. Например:

;

;

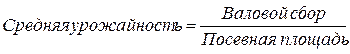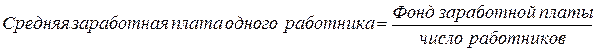Такой подход позволяет правильно определить среднюю величину признака, выбрать форму средней.

В статистике используются различные виды средних величин: арифметическая, гармоническая, геометрическая, хронологическая, квадратическая.

Наиболее распространённым видом средних величин в статистике является средняя арифметическая.

А. Средняя арифметическая.

Средняя арифметическая бывает в двух видах: средняя арифметическая простая и средняя арифметическая взвешенная.

Средняя арифметическая простая равна сумме отдельных значений признака, делённой на число этих значений.

В статистике отдельные значения изучаемого признака называются вариантами и обозначаются через Х (Х₁, Х₂, Х₃), число единиц в совокупности обозначаются через n, среднее значение признака – через . Отсюда, средняя арифметическая простая может быть представлена в виде:

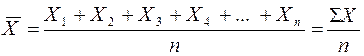
Типовая задача № 1.

Имеются следующие данные о размерах торговой площади магазинов:

Таблица 4.5

Магазины
Торговая площадь, м^2

Определите среднюю торговую площадь одного магазина.

Решение:

Для определения средней площади магазина / / необходимо сложить площади всех /10/ магазинов и полученный результат разделить на число магазинов.

.

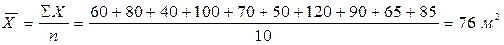Таким образом, средняя торговая площадь одного магазина составит 76м².

В нашем примере каждая варианта /Х/ повторяется один раз. Если в изучаемой совокупности варианты повторяются, то среднюю арифметическую можно рассчитать проще: нужно перед суммированием умножить значение признака (варианта) на число единиц, которым это значение присуще /Хƒ/ и полученную сумму разделить на сумму весов или частот /∑ƒ/. Отсюда средняя арифметическая взвешенная может быть представлена в виде:

.

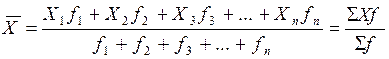Типовая задача № 2.

Имеются следующие данные о заработной плате рабочих-сдельщиков:

Таблица 4.6

Месячная заработная плата (грн., варианта Х)	Число рабочих (ƒ)	Х∙ƒ
Х1 = 100 Х2 = 120 Х3 = 150 Х4 = 170 Х5 = 200	= 2 = 6 = 16 = 12 = 4
Итого:

Данные представлены в виде дискретного ряда распределения, по которому видно, что одни и те же значения признака (варианты) повторяются несколько раз. Так, варианта Х₁ встречается в совокупности 2 раза, а варианта Х₃ – 16 раз и т. д.

Исчислим среднюю заработную плату одного рабочего ():

Статистический материал в результате обработки может быть представлен не только в виде дискретных рядов распределения, но и в виде интервальных вариационных рядов с закрытыми или открытыми интервалами. Рассмотрим расчёт арифметической для таких рядов.

Типовая задача № 3.

Имеются следующие данные:

Таблица 4.7

Группы рабочих по количеству произведённой продукции за смену (штук) (Х)	Число рабочих (ƒ)	Середина интервала ()	Х·ƒ
3 - 5 5 - 7 7 - 9 9 - 11 11 - 13
Итого:

Исчислим среднюю выработку продукции одним рабочим за смену. В данном ряду варианты усредняемого признака (продукции за смену) представлены не одним числом, а в виде интервала "от – до". Рабочие первой группы производят продукцию от 3 до 5 штук, рабочие второй группы – от 5 до 7 штук и т. д. Таким образом, каждая группа распределения имеет нижнее и верхнее значение вариант, или закрытые интервалы. Исчисление средней по сгруппированным данным производится по формуле средней арифметической взвешенной:

.

Чтобы применить эту формулу, необходимо варианты признака выразить одним числом (дискретным). За такое дискретное число принимается средняя арифметическая простая из верхнего и нижнего значения интервала. Так, для первой группы дискретная величина будет равна:

Дальнейший расчёт производится обычным методом определения средней арифметической взвешенной:

Итак, все рабочие произвели 750 штук изделий за смену, а каждый в среднем произвёл по 7,5 штуки.

Преобразуем рассмотренный выше ряд распределения в ряд с открытыми интервалами.

Типовая задача № 4.

Имеются следующие данные о производстве продукции за смену:

Таблица 4.8

Группы рабочих по количеству произведённой продукции за смену (штук)	Число рабочих
до 5 5 - 7 7 - 9 9 - 11 свыше 11
Итого:

В таких рядах условно принимается величина интервала первой группы равная величине интервала последующей, а величина интервала последней группы равная величине интервала предыдущей. Дальнейший расчёт аналогичен изложенному выше.

Б. Средняя гармоническая.

В статистике при обобщении общественных явлений и процессов наряду со средней арифметической широко применяется средняя гармоническая. Средняя гармоническая по своей форме является величиной, обратной средней арифметической. В зависимости от характера имеющегося материала, среднюю гармоническую формулу применяют тогда, когда в исходных данных частоты вариант усредняемого признака непосредственно не заданы, а входят как сомножитель в один из имеющихся показателей (Х), т. е. произведение вариант на частоты (Хƒ) и ещё заданы сами варианты (Х).

Как и средняя арифметическая, средняя гармоническая может быть простой и взвешенной.

Если даны варианты (Х) и произведение вариант на частоты (Х·ƒ), которые равны между собой, то применяется средняя гармоническая простая, которая имеет следующий вид:

,

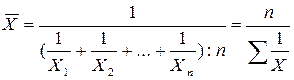где: n - число варианта; Х - варианты.

Типовая задача № 1.

Имеются следующие данные о ценах и сумме продажи товаров "А" на рынках:

Таблица 4.9

Рынки	Цена за единицу, грн (Х)	Продано, грн. (Х·ƒ)
I II

Определите среднюю цену единицы товара "А".

Решение:

Таким образом, средняя цена товара "А" составит 2,4 грн.

Если даны варианты (Х) и произведение вариант на частоты (Х·ƒ) и последние не равны между собой, то применяется средняя гармоническая взвешенная, которая имеет следующий вид:

,

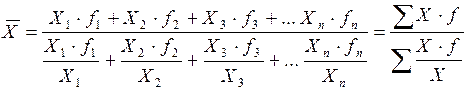если (Х·ƒ) обозначить через М, тогда формула будет иметь следующий вид:

.

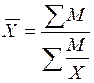Типовая задача № 2.

Имеются следующие данные о ценах и сумме продажи товара "А" на рынках:

Таблица 4.10

Рынки	Цена за единицу, грн (Х)	Продано, грн. (Х·ƒ)
I II

Определите среднюю цену единицы товара "А".

Решение:

Таким образом, средняя цена единицы товара "А" равна 2,33 грн.

В. Средняя геометрическая.

Средняя геометрическая применяется при расчёте средних темпов изменения явления во времени. Расчёт производится по формуле:

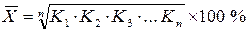или ,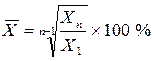

где К₁, К₂, К₃… К_n – коэффициенты динамики по отношению к предыдущему периоду;

n – число коэффициентов динамики;

Х₁ и Х_n – соответственно первый и последний абсолютные уровни ряда динамики.

Типовая задача № 1.

Имеются следующие данные выпуска литья в оболочных формах в литейном цехе завода за пятилетний период:

Таблица 4.11

Годы	1-й	2-й	3-й	4-й	5-й
Выпуск литья, тонн	230,1	243,8	261,5	285,8	286,6
В % к предыдущему году	—	105,9	107,3	109,3	100,3

Требуется определить средний темп выпуска литья.

Решение

Таким образом, средний темп роста выпуска литья составил 105,6 %.

Г. Средняя хронологическая.

Средняя хронологическая применяется на практике для определения среднегодовой численности населения, среднегодовой численности скота, фуражных коров, среднего размера остатков оборотных средств среднесписочного числа рабочих и служащих и т.п. Средняя хронологическая исчисляется по формуле:

,

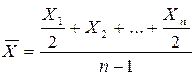где Х - абсолютные уровни,

n - число абсолютных уровней.

Типовая задача № 1.

Имеются следующие данные о поголовье крупного рогатого скота на 1 января:

Таблица 4.12

Показатель	2001 г.	2002 г.	2003 г.	2004 г.	2005 г.
Крупный рогатый скот (тыс. голов)	99,2	102,4	104,0	106,3	109,1

Определите среднегодовое поголовье крупного рогатого скота.

Решение:

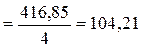тыс. голов.

Таким образом, среднегодовое поголовье скота составит 104,21 тыс. голов.

Д. Средняя квадратическая.

Средняя квадратическая применяется в тех случаях, когда в исходной информации усредняемые величины представлены линейными мерами. Например, при расчёте средних диаметров труб, стволов деревьев и т.д. Формула её расчёта следующая:

простая ,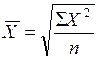

взвешенная .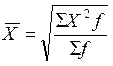

Дата добавления: 2014-11-08