Сущность и показатели вариации

Вариация – это колеблемость признака около средней величины.

Основными показателями вариации являются:

а) размах вариации (R);

б) среднее линейное отклонение ();

в) дисперсия (σ²);

г) среднее квадратическое отклонение (σ);

д) коэффициент вариации (V).

Размах вариации (R) – есть разность между наибольшим (X _max) и наименьшим (X _min) значениями признака в ряду распределения:

R = X _max – X _min

Например, возраст самого молодого студента составляет 17 лет, а самый старший – 26 лет. Разность составит 9 лет.

По величине размаха вариации можно судить о различии между передовыми и отстающими. Например, если самый передовой рабочий выполняет план на 220 %, а самый отстающий – на 80 %, то разность составит 140 %.

Однако этот показатель имеет тот существенный недостаток, что он полностью зависит от отдельных случаев, оказавшиеся на обоих полюсах ранжированного ряда. Между тем, отдельные случаи не всегда достаточно характерны, и опора на них может дать превратное представление о характере колеблемости. Поэтому возникает необходимость в другом показателе, который опирался бы не на одни только крайние значения, а и на значения определённого признака в данной совокупности. Таким показателем является среднее линейное отклонение ().

Среднее линейное отклонение представляет собой среднюю величину отклонений значений признака от их средней величины. При его расчёте все отклонения берутся со знаком плюс. Расчёт производится по формулам:

простое ,

взвешенное .

Из приведенного выше примера эти отклонения можно представить в графической форме (рис. 5.2).

Из графика видно, что на предприятии № 1 отклонения незначительны, а на предприятии № 2 – велики. Как же можно одним показателем характеризовать размер этих отклонений? Если все эти отклонения сложить, то в сумме получим нуль, так как известно, что сумма отклонений от средней арифметической равна нулю. Если эти отклонения возвести в квадрат, то получим все значения положительными.

Рис. 5.2. Процент выполнения плана по дням недели

на двух предприятиях.

Представим квадраты отклонений в следующей графической форме (рис. 5.3).

Понедельник Вторник Среда Четверг Пятница

Рис. 5.3. Квадраты отклонений выполнения плана

по двум предприятиям в процентах (по первому они равны 1² + 2,5² + 2,5² +1² +2², т. е. 1 +6,25 +6,25 +1 +4; по второму предприятию соответствующие цифры приведены на графике внутри квадратов).

Получив квадраты разной величины, необходимо исчислить показатель, который характеризовал бы средние размеры квадратов. По каждому предприятию для этого надо сложить площади квадратов и разделить на их число, т. е. мы определяем такой показатель как дисперсия.

Дисперсия, или средний квадрат отклонений вариантов признака от их средней величины, вычисляется по формулам:

простая или ;

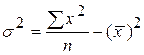взвешенная или .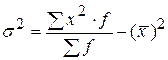

Затем, возвращаясь к линейному измерению, надо из величины дисперсии извлечь квадратный корень и мы получим наиболее точный показатель – среднее квадратическое отклонение. В нашем примере – это будет величина стороны квадрата.

Среднее квадратическое отклонение вычисляется по формуле:

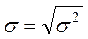или простое ;

взвешенное .

В отличие от среднего линейного и среднего квадратического отклонения коэффициент вариации является мерой относительной колеблемости признака около средней величины и характеризует степень однородности признака в изучаемой совокупности. Он определяется по форме:

или .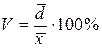

Если коэффициент вариации ≥ 33,3 %, тогда исследуемая совокупность считается неоднородной и должна быть разгруппирована.

Рассмотрим вычисление показателей вариации на примере.

Типовая задача № 1.

Имеются следующие данные о производительности труда рабочих в двух бригадах:

Таблица 5.2

Табельный номер рабочего	Произведено продукции за смену (штук)
I бригада	II бригада
Итого

Определите показатели вариации.

Решение:

Для нашего примера размах вариации производительности труда для первой бригады составляет: R₁ = 18 – 2 = 16; для второй бригады: R₂ = 12 – 8 = 4.

Этот показатель прост в вычислении и указывает на общие размеры вариации, но он не даёт представления о степени колеблемости внутри совокупности, так как вычисляется на основе только двух крайних значений признаков совокупности.

Исчислим среднее линейное отклонение.

Порядок расчёта среднего линейного отклонения следующий:

1. по значениям признака исчисляется средняя арифметическая:

;

2. определяются отклонения каждого варианта (Х) от средней:

;

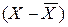3. рассчитывается сумма абсолютных отклонений:

;

4. сумма абсолютных отклонений делится на число значений:

.

Произведя арифметические действия мы получим:

Таблица 5.3

Табельный номер рабочего	I бригада	II бригада
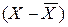
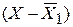
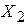
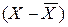
		-8 -7 +2 +5 +8			-2 -1 +1 +2
Итого:

Тогда среднее линейное отклонение для I бригады составит: 30:5 = 6 шт., для II бригады – 6:5 = 1,2 шт.

Исчислим дисперсию.

Порядок расчёта дисперсии невзвешенной следующий:

1. определяется средняя арифметическая:

;

2. рассчитываются отклонения вариант от средней:

;

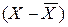3. возводятся в квадрат отклонения вариантов средней:

;

4. суммируются квадраты отклонений:

;

5. полученная сумма делится на число вариант:

.

Произведя арифметические действия получим:

Таблица 5.4

Табельный номер рабочего	I бригада	II бригада
кол-во продукции (штук)		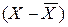	кол-во продукции (штук)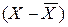
		-8 -7 +2 +5 +8			-2 -1 +1 +2
Итого:

Тогда дисперсия для I бригады будет равна – 206:5 = 41,2 шт., а для II бригады – 10:5 = 2 шт.

Определяем среднее квадратическое отклонение по формуле:

.

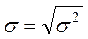Тогда среднее квадратическое отклонение для I бригады будет равно шт., а для II бригады шт.

Определяем коэффициент вариации по формуле:

.

Тогда, для I бригады он будет равен , а для II бригады .

По величине коэффициента вариации можно судить о степени вариации признаков совокупностей. Чем больше его величина, тем больше разброс значений признаков вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.

Если совокупность разбита на группы (или части) по изучаемому признаку, то для такой совокупности могут быть исчислены следующие виды дисперсии: групповые (частные), средняя из групповых (частных), межгрупповая.

Групповая (частная) дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы от средней арифметической этой группы (групповой средней). Она может быть исчислена как простая средняя или взвешенная соответственно по формулам:

, .

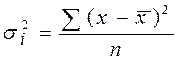Эта дисперсия отражает вариацию признака только за счёт условий и причин, действующих внутри группы.

Средняя из групповых (частных) дисперсия – это средняя арифметическая, взвешенная из дисперсия групповых:

.

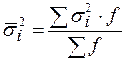Межгрупповая дисперсия равна среднему квадрату отклонений групповых средних от общей средней :

.

Межгрупповая дисперсия характеризует вариацию результативного признака за счёт группировочного признака.

Между указанными видами дисперсий существует определённое соотношение: общая дисперсия равна сумме средней из групповых дисперсий и межгрупповой дисперсии:

.

Это соотношение называют правилом сложения дисперсий. С его помощью, зная два вида дисперсий, можно определить третий:

Поясним правило сложения дисперсий на примере.

Типовая задача № 2.

Имеются следующие данные о производительности ткачей за час работы:

Таблица 5.5

Табельн. номер ткача	Изготовл. ткани трёх станочник. за час работы (Х), вариант			Табельн. номер ткача	Изготовл. ткани четырёх стан. за час работы (Х), вариант
		-2 -1				-3 -2 -1
Итого:

Исчислим:

1) групповые дисперсии;

2) среднюю из групповых дисперсий;

3) межгрупповую дисперсию;

4) общую дисперсию.

1. Для расчёта групповых дисперсий исчислим средние по каждой группе:

; ;

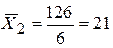Расчёт дисперсий по группам представлен в таблице. Подставив полученные значения в формулу, получим:

; .

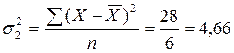2. Рассчитаем среднюю из групповых (частных) дисперсий:

.

3. Исчислим межгрупповую дисперсию. Для этого предварительно определим общую среднюю как среднюю взвешенную из групповых средних:

.

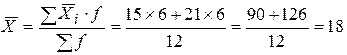Затем рассчитаем межгрупповую дисперсию:

.

4. Исчислим общую дисперсию по правилу сложения дисперсий:

Проверим полученный результат, исчислив общую дисперсию обычным способом:

.

Дата добавления: 2014-11-08