Основные показатели рядов динамики

В статистике для того, чтобы выявить особенности развития изучаемых явлений и процессов за отдельные периоды времени, исчисляются абсолютные и относительные показатели изменения ряда динамики:

а) абсолютные приросты;

б) средний абсолютный прирост;

в) абсолютное значение одного процента прироста;

г) темп роста;

д) темп прироста;

е) средний темп роста;

ж) средний темп прироста.

В основе расчёта показателей рядов динамики лежит сравнение его уровней. В зависимости от применяемого способа сопоставления показатели динамики могут вычисляться на постоянной и переменной базах сравнения.

Для расчёта показателей динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. Исчисленные при этом показатели называются базисными. Для расчёта показателей динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели динамики называются цепными.

1. Абсолютный прирост (Δy) – это разность между уровнями данного периода и периода, принятого за базу сравнения (предыдущего периода). Он вычисляется по формулам:

а) базисный

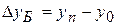
б) цепной

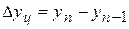
где: 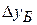– абсолютный прирост базисный;

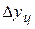– абсолютный прирост цепной;

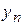– уровень сравниваемый;

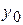– уровень периода, принятого за базу сравнения;

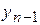– уровень, предшествующий сравниваемому периоду.

2. Средний абсолютный прирост представляет собой обобщённую характеристику индивидуальных абсолютных приростов ряда динамики. Он определяется по формулам:

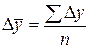или ,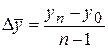

где n – число показателей в периоде.

3. Абсолютное значение одного процента прироста (А) характеризует абсолютный эквивалент одного процента прироста и определяется по формуле:

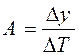, где 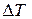– темп прироста.

4. Темп роста (Т) характеризует средний относительный рост явления за рассматриваемый период. Он рассчитывается по формуле:

; .

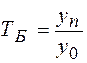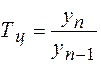5. Темп прироста (ΔТ) характеризует относительный прирост явления в отчётном периоде по сравнению с тем уровнем, с которым осуществляется сравнение. Он определяется по формулам:

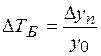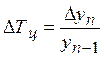; или

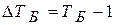(или 100 %); 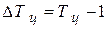(или 100 %).

6. Средний темп роста (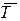) определяют по формуле средней геометрической двояким способом – на основе данных цепных коэффициентов динамики либо на основе данных абсолютных уровней ряда динамики по формулам:

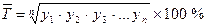или

.

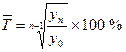7. Средний темп прироста (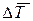) определяется на основе взаимосвязи между темпами роста и прироста:

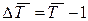(или 100 %).

Типовая задача № 1.

Имеются следующие данные о производстве зерна:

Таблица 6.9

Годы
Производство зерна, (тыс. тонн)

Требуется определить:

а) абсолютный прирост;

б) темп роста и прироста;

в) абсолютное значение одного процента прироста;

г) средний абсолютный прирост;

д) среднегодовой темп роста и прироста.

Решение:

1. Исчисляем абсолютные приросты с 2000 г. и по годам (тыс. тонн):

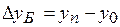2001 г. 168 – 150 = 18 2002 г. 179 – 150 = 29 2003 г. 186 – 150 = 36 2004 г. 191 – 150 = 41

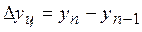168 – 150 = 18 179 – 168 = 11 186 – 179 = 7 191 – 186 = 5

2. Определяем темпы роста:

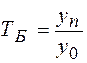2001 г. 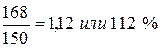2002 г. 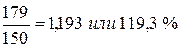2003 г. 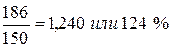2004 г.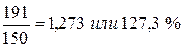

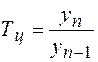
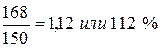
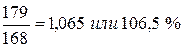
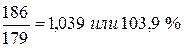
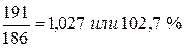
3. Определяем темпы прироста:

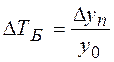2001 г. 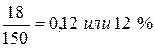2002 г. 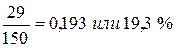2003 г. 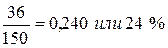2004 г.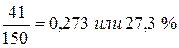

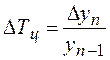
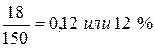
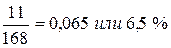
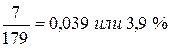
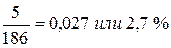
или вторым способом:

2001 г. 1,12 – 1 = 0,12 или 12 % 2002 г. 1,193 – 1 = 0,193 или 19,3 % 2003 г. 1,24 – 1 = 0,24 или 24 % 2004 г. 1,273 – 1 = 0,273 или 27,3 %	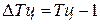1,12 – 1 = 0,12 или 12 % 1,065 – 1 = 0,065 или 6,5 % 1,039 – 1 = 0,039 или 3,9 % 1,027 – 1 = 0,027 или 2,7 %

4. Исчисляем абсолютное значение одного процента прироста (тыс. тонн):

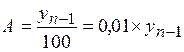
2001 г.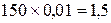

2002 г.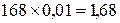

2003 г.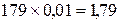

2004 г.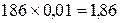

5. Исчисляем средний абсолютный прирост (тыс. тонн):

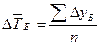
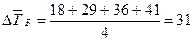
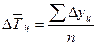
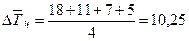
или по другой формуле:

6. Определяем значение среднегодового темпа роста:

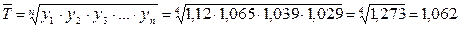
или 106,2 % или по формуле:

или 106,2 %.

7. Определяем среднегодовой темп прироста:

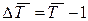
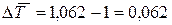или 6,2 %.

Результаты всех решений приведём в следующей таблице:

Таблица 6.10

Годы	Производство зерна (тыс. тонн)	Абсолютные приросты, (тыс. тонн)	Темпы роста, (%)	Темпы прироста, (%)
по сравнению с 2000 г.	по годам	по сравнению с 2000 г.	по годам	по срав- нению с 2000 г.	по годам
		—	—	100,0 112,0 119,3 124,0 127,3	— 112,0 106,5 103,9 102,7	— 12,0 19,3 24,0 27,3	— 12,0 6,5 3,9 2,7
Итого				—	—	—	—
В среднем	174,8		10,25	—	106,2	—	6,2

Дата добавления: 2014-11-08