Ошибки репрезентативности и способы их вычисления

Чтобы определить степень точности выборочного наблюдения, нужно оценить расхождения между средними и относительными показателями выборочной и генеральной совокупности, которые имеют место даже в случае отсутствия ошибок регистрации. Эти расхождения называются ошибками репрезентативности. Ошибки репрезентативности могут быть систематическими и случайными.

Систематические ошибки репрезентативности – это неточности, возникшие вследствие несоблюдения условий отбора единиц в выборочную совокупность, равной возможности каждой единицы генеральной совокупности попасть в выборку.

Случайные ошибки репрезентативности – это погрешности, возникающие вследствие того, что выборочная совокупность не воспроизводит в точности размеры средних и относительных показателей генеральной совокупности в силу несплошного характера обследования.

Средняя ошибка выборки для средней показывает расхождение выборочной и генеральной средней:

1. При бесповторном случайном отборе она рассчитывается по формуле:

,

где M – средняя ошибка выборочной средней;

n – численность выборки;

N – численность генеральной совокупности;

σ² – дисперсия выборочной совокупности.

Предельная ошибка выборки () рассчитывается по формуле: , где t – коэффициент доверия, зависит от значения вероятности (Р).

При Р = 0,997 t =3,

при Р = 0,954 t =2,

при Р =0,683 t =1.

Типовая задача № 1.

В районе А проживает 2500 семей. В порядке случайной бесповоротной выборки проведено обследование 50 семей. В результате обследования получены следующие данные о размере семьи:

Число детей в семье
Количество семей

Рассчитаем среднее число детей в семье в выборочной совокупности и дисперсию выборочной совокупности (табл.: 7.1).

Таблица 7.1.

Число детей в семье, (Х)	Кол-во семей, ()
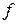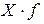
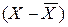
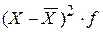
			-1,5 -0,5 +0,5 +1,5 +2,5 +3,5	2,25 0,25 0,25 2,25 6,25 12,15	22,5 5,0 3,0 9,0 12,5 24,5
Итого:			—	—	76,5

человека,

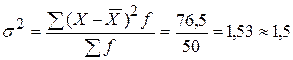человека.

Средняя ошибка выборки составит:

человека.

С вероятностью 0,997 рассчитаем предельную ошибку выборочной среды. Значение t определяется по таблице интеграла вероятностей.

При Р = 0,997, t = 3,

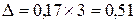человека.

Определим пределы, в которых находится среднее число детей в семье в районе А:

,

.

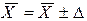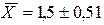Генеральная средняя () находится в пределах .

С вероятностью 0,997 можно утверждать, что число детей в семьях района А колеблется от 0,99 до 2,01 человека.

2. При случайном повторном отборе средняя ошибка выборочной средней рассчитывается по формуле:

.

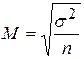Типовая задача № 2.

Методом случайной повторной выборки было взято для проверки на вес 200 штук деталей. В результате проверки был установлен средний вес детали (30 г.) при среднем квадратическом отклонении 4 г. С вероятностью 0,954 требуется определить предел, в котором находится средний вес деталей в генеральной совокупности.

Рассчитаем среднюю ошибку выборочной средней:

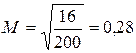(гр.)

Предельная ошибка выборочной средней с вероятностью 0,954 составит:

(г.).

Определим верхнюю границу генеральной средней:

30 + 0,56 = 30,56 (г.).

Определим нижнюю границу генеральной средней:

30 - 0,56 = 29,44 (г.).

С вероятностью 0,954 можно утверждать, что средний вес детали колеблется в пределах:

.

3. Ошибка выборочной доли при случайном бесповторном отборе рассчитывается по формуле:

,

где - доля единиц выборочной совокупности, обладающих изучаемым признаком.

Типовая задача № 3.

При разработке материалов городского населения методом случайного бесповторного отбора было установлено, что в городе А 15 % жителей старше 60 лет. Из общей численности населения города (500 тыс. человек) было отобрано 50 тыс. человек.

С вероятностью 0,683 определите предел, в котором находится доля жителей города А в возрасте старше 60 лет.

Рассчитаем среднюю ошибку выборочной доли:

.

С вероятностью 0,683 предельная ошибка выборочной доли составит:

(или 4,8 %).

Определим верхнюю границу генеральной доли:

0,15 + 0,048 = 0,198 (или 19,8 %).

Определим нижнюю границу генеральной доли:

0,15 - 0,048 = 0,102 (или 10,2 %).

С вероятностью 0,683 можно утверждать, что доля жителей в возрасте старше 60 лет в городе А колеблется от 10,2 до 19,7 %:

10,2 % < P < 19,8 %

5. При повторном отборе средняя ошибка выборочной доли рассчитывается по формуле:

.

В практике проектирования выборочного наблюдения возникает потребность определения численности выборки, которая необходима для обеспечения определённой точности расчёта средних величин. Предельная ошибка выборки и её вероятность при этом является заданными.

6. Необходимая численность выборки при бесповторном случайном отборе для определения выборочной средней с определённой точностью вычисляется по формуле:

.

Типовая задача № 4.

В районе А проживает 2000 семей. В порядке случайной бесповторной выборки предполагается определить средний размер семьи при условии, что ошибка выборочной средней не должна превышать 0,8 с вероятностью Р = 0,954 и при среднем квадратическом отклонении 2,0.

Рассчитаем необходимую численность выборки:

семьи.

7. При повторном случайном отборе численность выборки определяется по формуле:

.

Типовая задача № 5.

Для определения средней длины детали необходимо провести выборочное обследование методом случайного повторного отбора. Какое количество деталей надо отобрать, чтобы ошибка выборки не превышала 2 мм с вероятностью 0,954 при среднем квадратическом отклонении 8 мм.

Рассчитаем необходимую численность выборки:

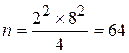детали.

Дата добавления: 2014-11-08