Основные понятия и определения. Свет как волновой процесс

Свет как волновой процесс.

Понятие волна неразрывно связано с понятием колебание. Колебания – это самый распространённый вид движения материи в природе. Они возникают у физических систем, имеющих положение или состояние равновесия, в которых они обладают минимумом энергии. При сообщении таким системам энергии извне, они вовлекаются в колебательный процесс. Подобные системы носят название осцилляторов.

Колебания могут быть свободными и вынужденными. Первые возникают при однократном возбуждении осциллятора, т.е. однократном сообщении ему энергии. Свободные электромагнитные колебания возникали в опыте Г.Герца в момент проскакивания искры в воздушном промежутке разрядника. Такие же колебания возникают при подключении предварительно заряженного конденсатора к катушке индуктивности. Свободные колебания являются затухающими, поскольку имеет место уменьшение энергии колебаний вследствие излучения в окружающую среду и потерь омического характера. Частоту таких колебаний называют собственной.

Вынужденные колебания возникают при периодическом энергетическом воздействии на колеблющуюся систему. Они являются незатухающими, поскольку имеет место периодическое пополнение естественной убыли энергии осциллятора. Если частота внешнего энергетического воздействия совпадает с собственной частотой системы, то наступает явление резонанса, при котором потери энергии становятся минимальными, а амплитуда колебаний – максимальной.

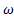Простейшими колебаниями, которые имеют место у осцилляторов, являются гармонические, т.е. колебания, совершаемые по закону синуса или косинуса: ξ , где ξ (кси)– отклонение некой физической величины от равновесного положения или состояния, A – максимальное значение этого отклонения по модулю (амплитуда), – фаза колебания, – круговая частота, рад 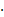с^-1, 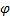– начальная фаза (значение фазы колебания в момент времени =0). Фаза колебания, будучи аргументом тригонометрической функции, определяет значение отклонения в данный момент времени. Начальная фаза при соответствующем выборе начала отсчёта может быть равна нулю (на рисунке).

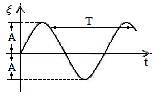Гармонические колебания являются периодическими функциями времени в том смысле, что в неограниченном интервале времени величина ξ принимает одно и то же значение при приращении фазы на . Промежуток времени, за который совершается это приращение, называют, периодом колебаний Т. Величину, показывающую сколько периодов колебаний совершается за одну секунду, называют просто частотой колебаний (ню), измеряемой в герцах: 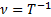,Гц, 1Гц=1с^-1 (в электротехнике частоту обычно обозначают как f). Между частотой и круговой частотой существует простая связь: . Колебания, совершаемые с одной частотой, называют монохроматическими.

Таким образом, амплитуда, фаза, начальная фаза, период и частота являются параметрами колебательного процесса.

Процесс распространения колебаний называют волной. Опыты Г.Герца показали, что электромагнитные волны могут неограниченно распространяться в пространстве, по этой причине их называют бегущими волнами. Бегущие волны являются носителями энергии, о чём свидетельствовало появление искры в разряднике удалённого вторичного контура в опыте Г.Герца. То расстояние, которая бегущая волна проходит за время, равное периоду, называют длиной волны, обозначаемой как и измеряемой в метрах (рис.2а). Длина волны колебаний, в свою очередь, также является параметром, но параметром только волны.

Поскольку частота электромагнитных колебаний очень велика, то в качестве параметра колебательного процесса используют не частоту колебаний, а длину волны. Если волна распространяется в пространстве со скоростью υ, то длина волны составит: 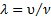. Так как скорость является векторной величиной, то и ЭМВ имеют определённую направленность, в связи с чем зачастую используют выражение электромагнитное излучение (ЭМИ). Луч – в данном случае – это линия, вдоль которой распространяется энергия излучения (волны), однако, строго говоря, использовать понятие луча можно лишь в случае с .

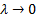Следует отметить, что то действие, которое свет оказывает на окружающий мир, а именно, биологическое, фотохимическое, фотогальваническое и др. – имеет место благодаря действию, в основном, электрического поля, а не магнитного. Поэтому вектор напряжённости электрического поля называют световым вектором, и именно его отклонение от состояния равновесия в дальнейшем будут обозначаться как .

Геометрическое место точек, до которых доходят колебания в данный момент времени, называют фронтом волны. Геометрическое место точек, в которых колебания совершаются в одной фазе, носит название волновой поверхности. Фронт волны всегда перемещается со скоростью υ, волновые же поверхности неподвижны.

Волновая поверхность может быть плоской (плоская волна) или сферической (сферическая волна). Тип волны, в данном случае, во многом зависит от пространственных характеристик возбудителя колебаний (источника колебаний) и расстояния до него. Если это расстояние много больше размеров источника, то источник колебаний называют точечным источником, и он будет генерировать сферическую волну. Если же размеры источника соизмеримы с расстоянием до приёмника излучения, то такой источник будет генерировать плоскую волну. Например, осветительная лампа накаливания имеет длину нити порядка сантиметра, следовательно, при расстоянии порядка метра от лампы (разница два порядка, что соответствует категории «много больше») она будет являться точечным источником, который генерирует сферическую волну. В то же время излучение дисплея сотового телефона будет представлять собой плоскую волну, поскольку размеры дисплея и расстояние от него до глаз пользователя сопоставимы.

Волновые поверхности плоской волны представляют собой бесконечное множество параллельных плоскостей, сферической – бесконечное множество концентрических сфер.

Зачастую колебательные процессы имеют сложный, негармонический характер, но если они представляют собой периодические функции времени, то их можно представить суперпозицией (совокупностью) гармонических колебаний. Каждое такое простейшее колебание гармонического характера и порождаемая им волна со своей пространственной конфигурацией носит название нормальной моды или просто моды. В известной степени понятие моды можно отождествлять с понятием гармоника.

Рис.1.Суперпозиция двух мод

На рис.1 представлен результат наложения двух монохроматических колебаний – мод 1 и 2 с частотами ₁ и ₂, причём ₁=3 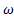₂. Результирующие колебания и порождаемая ими волна уже не является монохроматическими.

Распространяясь в пространстве, электрические и магнитные поля колеблются относительно состояния равновесия, каковыми являются нулевые значения векторов их напряжённостей. Таким образом, величины их отклонений от этих состояний являются, в данном случае, функциями не только времени, но и координат, т.е. . Данное выражение носит название уравнения волны.

Дата добавления: 2014-11-18