Уравнения плоской и сферической волн

Уравнение волны является функцией периодической не только относительно времени, но и относительно координат, поскольку точки пространства, отстоящие друг от друга на расстоянии λ, колеблются одинаково.

Найдём уравнение плоской монохроматической волны. Для этого направим ось x по направлению распространения волны (рис.2б). Тогда волновые поверхности (на рис.2б представлены две из них – 1 и 2) будут перпендикулярны оси х, и, поскольку все точки волновой поверхности колеблются одинаково, смещение будет зависеть только от x и : .

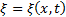Пусть колебания точек, лежащих в плоскости х =0, имеют вид:

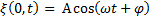(1)

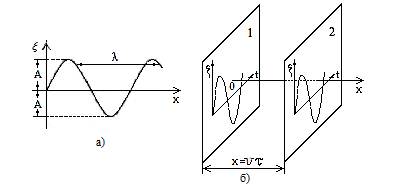  Рис.2. К выводу уравнения плоской волны

Расстояние от волновой поверхности 1 до волновой поверхности 2 волна проходит за время 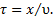Следовательно, колебания частиц, лежащих в плоскости 2, будут отставать от колебаний частиц в плоскости 1 на время :

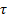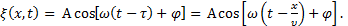(2)

Последнее выражение и есть уравнение плоской волны. Начальная фаза определяется выбором начала отсчёта х и .

Зафиксируем какое либо значение фазы, положив

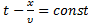→ . (3)

Это выражение связывает время с теми значениями х, в которых фаза имеет фиксированное значение. Если найти значение 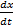, то, тем самым, найдём скорость, с которой перемещается данное значение фазы. Дифференцируя (3), имеем:

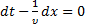, следовательно 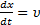(4)

Таким образом, то, что ранее называлось скоростью распространения волны, является, по сути, скоростью распространения фазы. Её называют фазовой скоростью. Поскольку в (4) 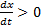, то это указывает на то, что волна распространяется в сторону возрастания x.

Для получения более компактного выражения (2) вводится так называемое волновое число 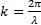. Умножив на , получим его модифицированное выражение: 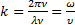. Тогда уравнение плоской волны (2) преобразуется следующим образом:

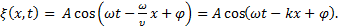(5)

Если волна распространяется в направлении убывания х, то выражение для фазы 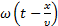и уравнение волны:

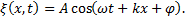(6)

Как следует из полученных выражений, амплитуда колебаний, а, следовательно, и их энергия, от х не зависит, т.е. волна может неограниченно распространяться и её энергия не поглощается средой. Если же волна проходит через поглощающую среду, то её энергия убывает по мере удаления от источника вследствие уменьшения амплитуды колебаний – как будет показано далее – по экспоненциальному закону (закону Бугера-Ламберта). В этом случае говорят – волна затухает.

Как отмечалось ранее, если расстояние до источника колебаний много больше его размеров, то источник считается точечным, В однородной и изотропной среде волна, порождаемая таким источником, будет сферической. Согласно волновым представлениям энергия точечного источника равномерно распределяется по волновой поверхности.

Допустим, фаза колебаний источника - 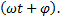Возьмём произвольную волновую поверхность радиуса r. Для того, чтобы дойти до неё волне потребуется время 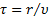. Следовательно, точки, расположенные на данной волновой поверхности, будут колебаться с фазой 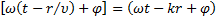. И если в случае с плоской волной амплитуда (и энергия) колебаний не зависят от х, то амплитуда колебаний сферических волн тесно связана с расстоянием до источника. Действительно, образующая волновой поверхности равна 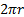и растёт с ростом r, а значит рост r будет вызывать уменьшение амплитуды колебаний по закону 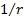. Таким образом, уравнение сферической волны будет иметь вид:

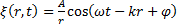, (7)

где А – амплитуда колебаний на расстоянии от источника, численно равного единице.

Уравнение любой волны является решением дифференциального уравнения, называемого волновым.

Дата добавления: 2014-11-18