Стандарты 2 страница

	Вариант 13	Вариант 14	Вариант 15
точки	X	Y	Z	точки	X	Y	Z	точки	X	Y	Z
A				A				A
B				B				B
C				C				C
D				D				D
E				E				E
F				F				F
	Вариант 16	Вариант 17	Вариант 18
точки	X	Y	Z	точки	X	Y	Z	точки	X	Y	Z
A				A				A
B				B				B
C				C				C
D				D				D
E				E				E
F				F				F

	Вариант 19	Вариант 20	Вариант 21
точки	X	Y	Z	точки	X	Y	Z	точки	X	Y	Z
A				A				A
B				B				B
C				C				C
D				D				D
E				E				E
F				F				F

	Вариант 22	Вариант 23	Вариант 24
точки	X	Y	Z	точки	X	Y	Z	точки	X	Y	Z
A				A				A
B				B				B
C				C				C
D				D				D
E				E				E
F				F				F

Основные теоретические сведения по теме.

Программой предусмотрено рассмотрение только одного ортогональ­ного (прямоугольного) метода проецирования. Он состоит в том, что все проецирующие лучи параллельны между собой и перпендикулярны плоскости проекций, так называется плоскость, на которую проецируется предмет.

Чтобы получить проекцию А₁ точки А на горизонтальной плоскости (которую будем обозна­чать греческой буквой П—пи), надо из точки А пространства опустить перпендикуляр. Точка пере­сечения перпендикуляра с плоскостью будет проекцией А₁ точки А. '

Плоскость П₁, будем называть горизонтальной плоскостью проекций, а перпендикуляр, опу­щенный из точки А, — проецирующим перпендикуляром. Надо иметь в виду, что если заданы одна плоскость проекций, например П₁, и на ней проекция А₁, то одной проекции недостаточно для того, чтобы определить положение точки в пространстве, так как одна и та же проекция принадлежит множеству точек, расположенных на проецирующем перпендикуляре А₁А (рис. 9).

Следовательно, для определения положения точки А по отношению плоскостей проекций, необходимо задать две проекции А₁ и А₂ точки А (рис. 10), которые начертеже (эпюре) будут расположены на одном перпендикуляре к оси проекций (рис. 11). Та же точка может быть спрое­цирована на три плоскости проекций П₁ П₂ и П₃ (рис. 12).

Прямая линия представляет собой множество точек, и для того чтобы ее спроецировать, достаточно иметь две ее точки.

Прямую, параллельную хотя бы одной из плоскостей проекций, называют прямой част­ного положения.

Прямую, не параллельную и не перпендикулярную ни одной из плоскостей проекций, на­зывают прямой общего положения (рис. 13).

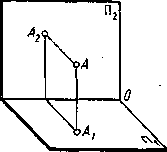
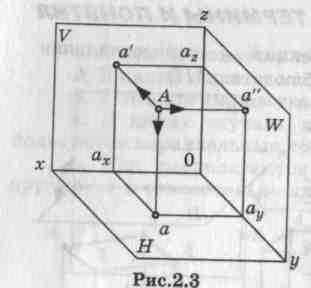
Рис.10 Рис.12.

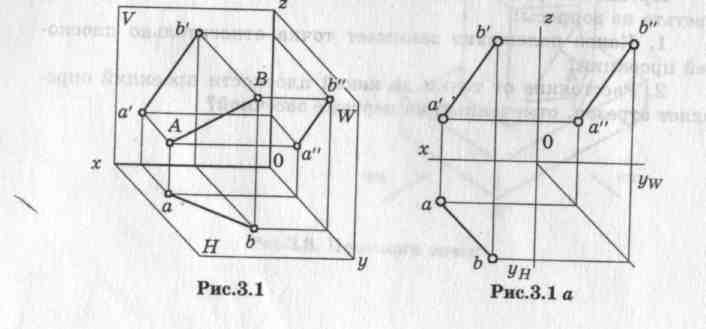
Рис. 13

Рис.13

Напомним свойства ортогонального (прямоугольного) метода проецирования:

1. Проекция точки есть точка.

2.Проекция прямой в общем виде всегда прямая (исключение — когда прямая пер- пендикулярна одной из плоскостей проекций).

3. Проекция точки делит проекцию отрезка в том же отношении, в каком точка делит этот отрезок в пространстве.

Надо хорошо знать и понимать взаимное положение прямых в пространстве. Их три: прямые параллельные, пересекающиеся и скрещивающиеся.

Напоминаем, что прямые, параллельные в пространстве, имеют параллельные проекции; прямые, пересекающиеся в пространстве, имеют одну общую точку, проекции которой на чертеже лежат на одном перпендикуляре к оси проекций; если прямые скрещивающиеся, то они не имеют общих точек и не параллельны между собой.

Если прямые в пространстве пересекаются под прямым углом, т. е. перпендикулярны, и если одна из прямых параллельна одной из плоскостей проекций, то прямой угол на эту плос­кость проецируется без искажения, т. е. также в виде прямого угла {рис. 14).

Надо очень хорошо знать, как можно задать плоскость на чертеже — тремя проекциями точек, не лежащих на одной прямой, проекциями двух параллельных прямых, проекциями двух пересекающихся прямых и, наконец, любой плоской фигурой.

Плоскости, как и прямые линии, могут быть общего и частного положения.

Необходимо хорошо усвоить принцип принадлежности (инцидентности).

1. Если прямая принадлежит плоскости, то она должна иметь с этой плоскостью две общие точки 1 и 2 (рис. 15).

2.Если точка Д принадлежит плоскости, то она должна принадлежать прямой А₁ лежащей в этой плоскости (рис. 16).

При проработке материала обратите особое внимание на прямые особого назначения, или главные линии плоскости.

Горизонталь h — прямая, лежащая в плоскости параллельно горизонтальной плоскости проекций (рис. 17). У горизонтали в плоскости общего положения фронтальная проекция параллельна оси проекций ОХ, в плоскости фронтально проецирующей фронтальная проекция горизонтали проецируется в виде точки.

Фронталь f—прямая, линия лежащая в плоскости параллельно фронтальной плоскости проекций (рис. 18). Горизонтальная проекция фронтали в плоскостях общего положения па­раллельная оси ОХ, в плоскости горизонтально-проецирующей (частного положения) горизон­тальная проекция изобразится в виде точки.

Линия наибольшего ската р — это линия, лежащая в плоскости перпендикулярно горизон­талям плоскости. Горизонтальная проекция линии ската перпендикулярна горизонтальной про­екции горизонтали (рис. 19). С помощью этой линии определяют угол наклона данной плоскости к горизонтальной плоскости проекций.

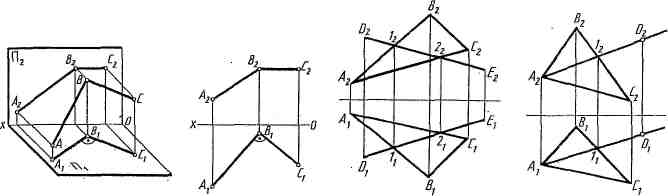
рис.14 рис. 15 рис.16

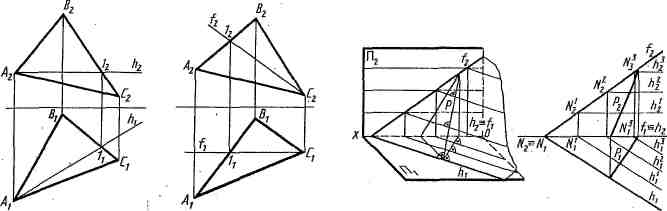
рис.17 рис 18 рис.19

Порядок выполнения.

1. Изучить методические указания, ГОСТы и соответствующую литературу.

2. Подготовить рабочее место, инструменты, бумагу и пособия.

3. Ознакомиться с содержанием индивидуального задания и образцом выполнения.

4. Наметить места расположения задания.

5. Построить по координатам точек плоскости α(АВС) и β (DFE).

6. Заключаем одну из сторон, например АС, во фронтально-проецирующую плоскость γ_2.

7. Находим линию пересечения 3-4.

8. Находим горизонтальную проекцию L₁, затем фронтальную проекцию L₂.

9. Сторону заключаем в горизонтально проецирующую плоскость σ_1.

10. Находим линию пересечения 1-2, а затем и точку К (К₁, К₂).

11. Определяем видимость по конкурирующим точкам.

Задание 4

«Проецирование группы геометрических тел.

Аксонометрическое изображение группы геометрическ их тел,»

Цель:

• ознакомиться с сутью метода проецирования.

• научиться выполнять комплексные чертежи геометрических тел.

• научиться выполнять аксонометрические проекции геометрических тел.

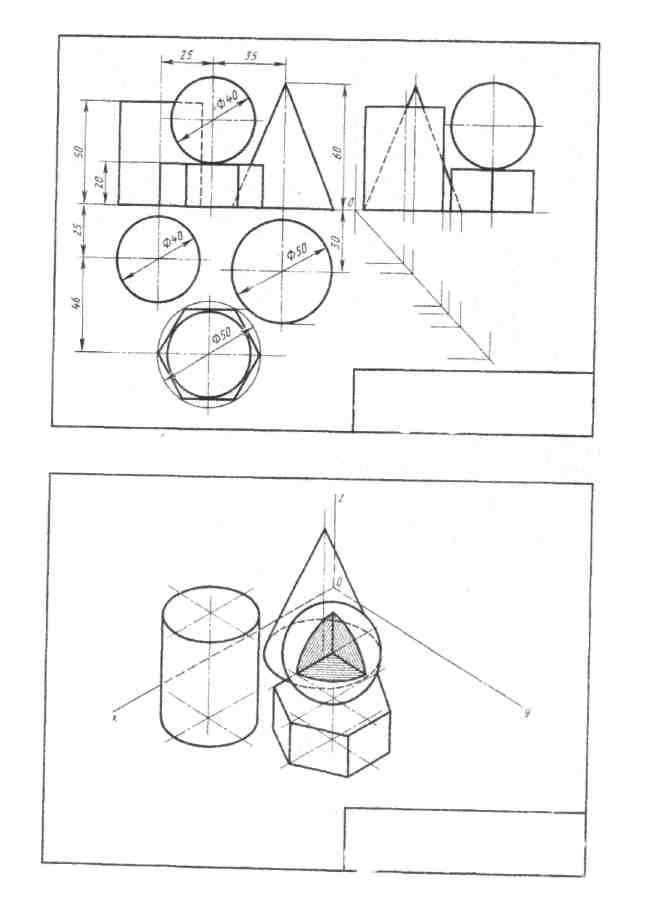
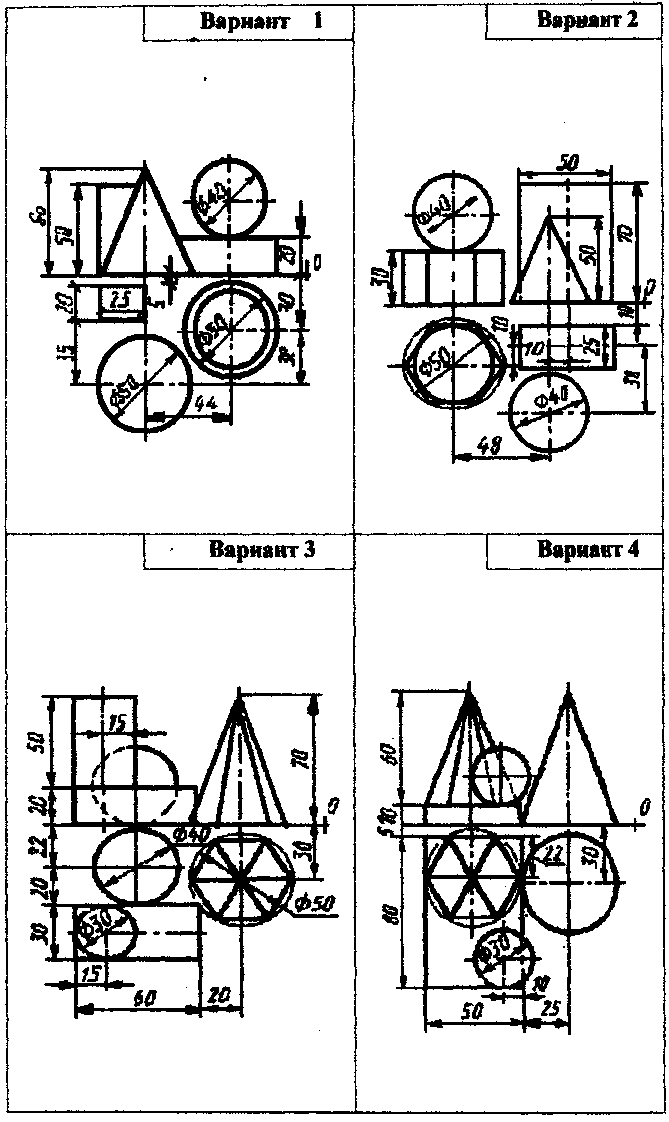
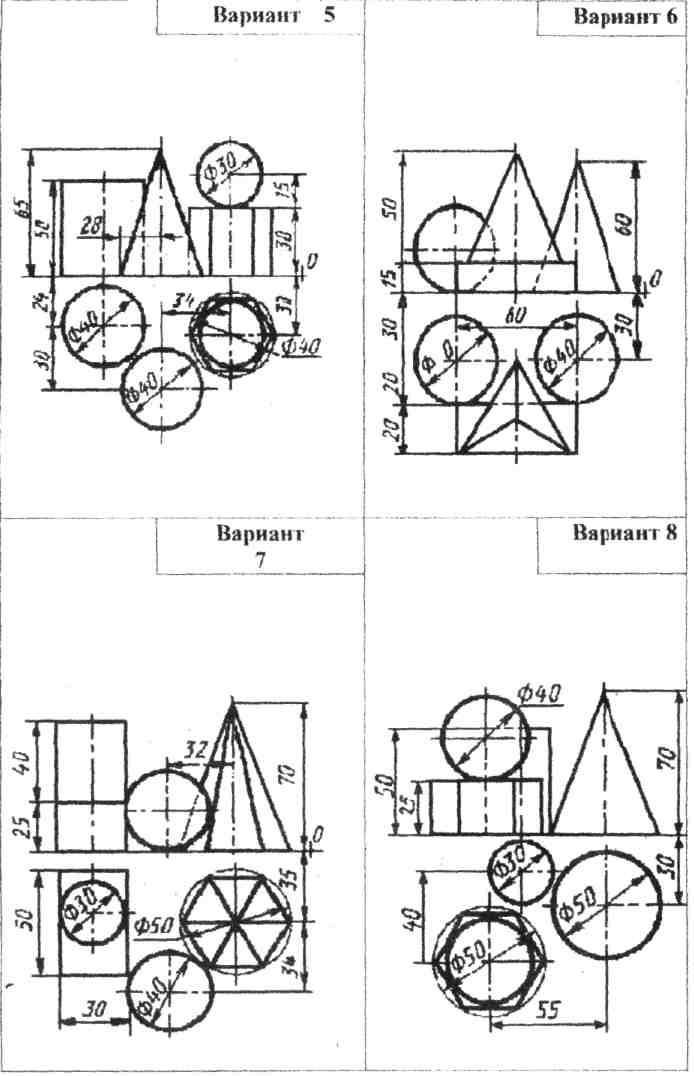
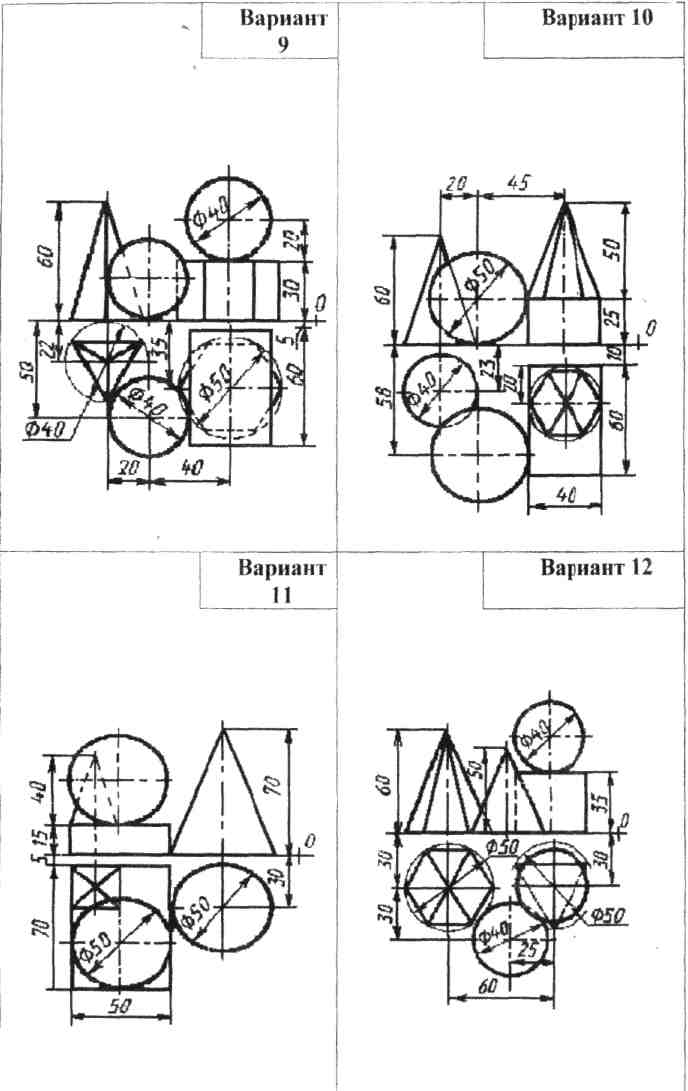
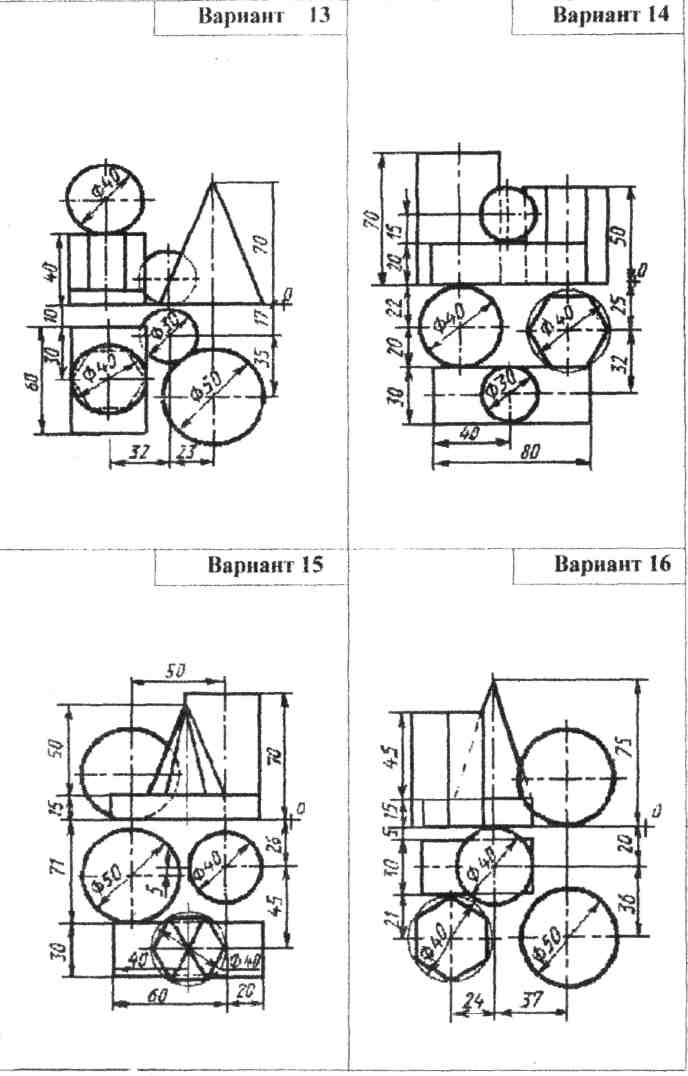
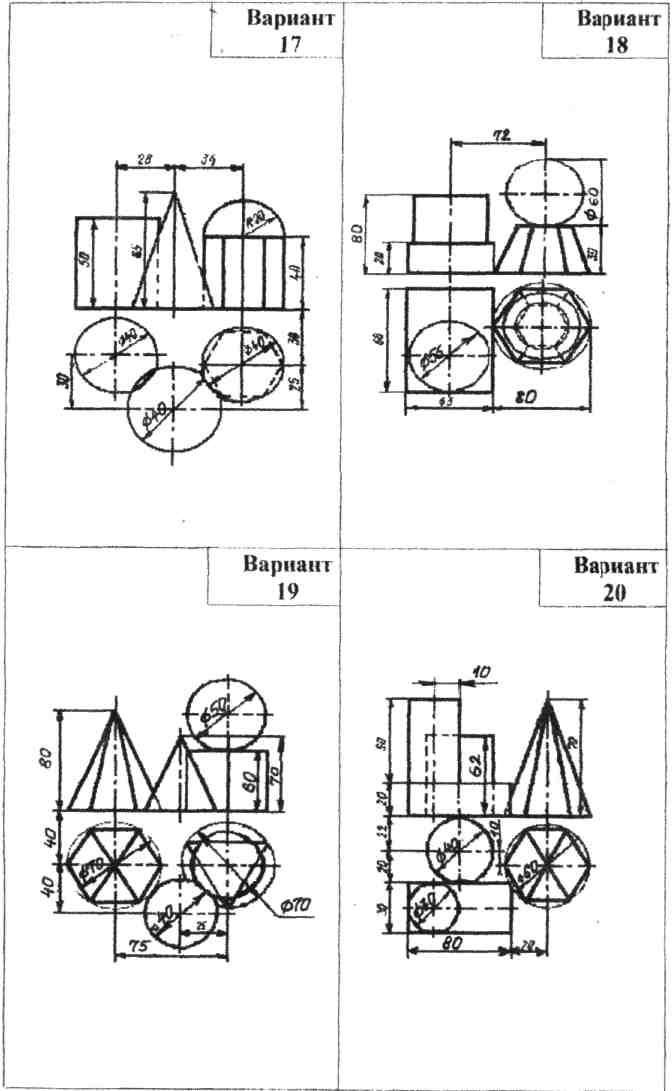
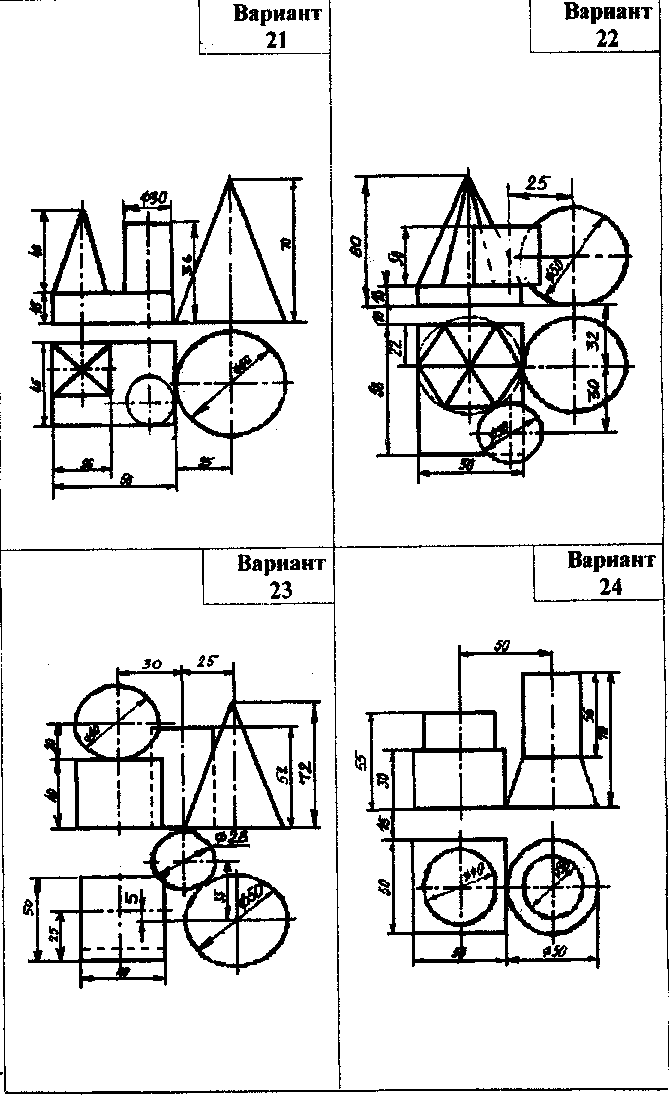
Содержание. Вычертить три проекции и аксонометрическое изображение группы геометрических тел на листе чертежной бумаги формата А3(297х420). Образец выполнения дан на рис. 6. Варианты графической работы приведены в таблице 2.

Основные теоретические сведения по теме «Проецирование»

Согласно ГОСТ 2.305-68 изображения предметов выполняются по методу прямоугольного проецирования на несколько плоскостей проекций. В практике выполнения чертежей предмет чаще всего проецируют на три основные плоскости проекций: фронтальную, горизонтальную и профильную.

Изображение предмета на плоскости, полученное при помощи проецирующих лучей, называют проекцией. На фронтальной плоскости проекции получают фронтальную проекцию предмета; на горизонтальной плоскости - горизонтальную проекцию; на профильной - профильную.

Проекции располагают в строгом порядке: горизонтальная проекция всегда располагается под фронтальной, профильная - на одной высоте с фронтальной, справа от нее. Это правило размещения проекций нарушать нельзя.

Основные теоретические сведения по теме «Проецирование геометрических тел»

Для того, чтобы при выполнении чертежей представить себе форму детали, удобно мысленно расчленять деталь на отдельные геометрические тела.

Геометрическое тело - часть пространства, ограниченная со всех сторон геометрической поверхностью.

Геометрические тела подразделяются на:

• многогранники (призма, пирамида)

• тела вращения (конус, цилиндр, тар, тор).

Геометрические тела, ограниченные плоскими фигурами - многоугольниками, называются многогранниками. Их стороны, плоские фигуры, называются гранями, а линии их пересечения - ребрами.

Призмой называется многогранник, две грани которого равные многоугольники, расположенные в параллельных плоскостях (основания призмы), а остальные грани -параллелограммы (боковые грани призмы) (рис. 7). Различают прямую н наклонную призмы.

Пирамидой называется многогранник, одна грань которого, называемая основанием, есть многоугольник, а остальные грани, называемые боковыми, есть треугольники с общей вершиной (рис. 8).

Если в основании пирамиды лежит правильный многоугольник, а высота пирамиды проходит через центр основания, то пирамида называется правильной.

Общее название призмы и пирамиды определяется формой их основания. Если, например, основание пирамиды или призмы треугольник, то речь идет о треугольной пирамиде или треугольной призме.

Телами вращения называются геометрические тела, ограниченные поверхностями вращения и плоскостями (цилиндр, конус) или только поверхностями вращения (шар, тор).

Цилиндром Называется геометрическое тело, ограниченное круговой цилиндрической поверхностью и двумя параллельными друг другу кругами, называемыми основаниями (рис.9). Если образующие цилиндра располагаются перпендикулярно основаниям, то цилиндр называется прямым, если под углом -наклонным.

Конусом называется геометрическое тело, ограниченное частью конической круговой поверхности, расположенной по одну сторону от вершины и кругом, называемым основанием конуса (рис. 10).

Если основание конуса расположено перпендикулярно оси вращения, то конус называется прямым, если под углом - то наклонным. Образующие конуса, являющиеся линиями контура проекций, называются очерковыми.

Часть пространства, ограниченная сферической поверхностью, называется шаром (рис. 11).

Поскольку форма большинства предметов представляет собой сочетание различных геометрических тел или их частей, для построения чертежей предметов необходимо знать, как изображается каждое геометрической тело.

Тела располагают относительно плоскостей проекций по возможности так, чтобы их основные элементы (ребра, грани, оси, основания) были параллельны или перпендикулярны плоскостям проекций. Тогда на одну из плоскостей проекций эти элементы будут проецироваться в натуральную величину

Построение проекций правильной промой призмы начинается с выполнения ее горизонтальной проекции - правильного многоугольника. Из вершин этого многоугольника проводят вертикальные линии связи и строят фронтальную проекцию нижнего основания призмы - отрезок горизонтальной прямой. От этой прямой вверх откладывают высоту призмы и строят фронтальную проекцию верхнего основания. Затем вычерчивают фронтальные проекции ребер - отрезки вертикальных прямых, равные высоте призмы. Далее строят профильную проекцию призмы (рис 12).

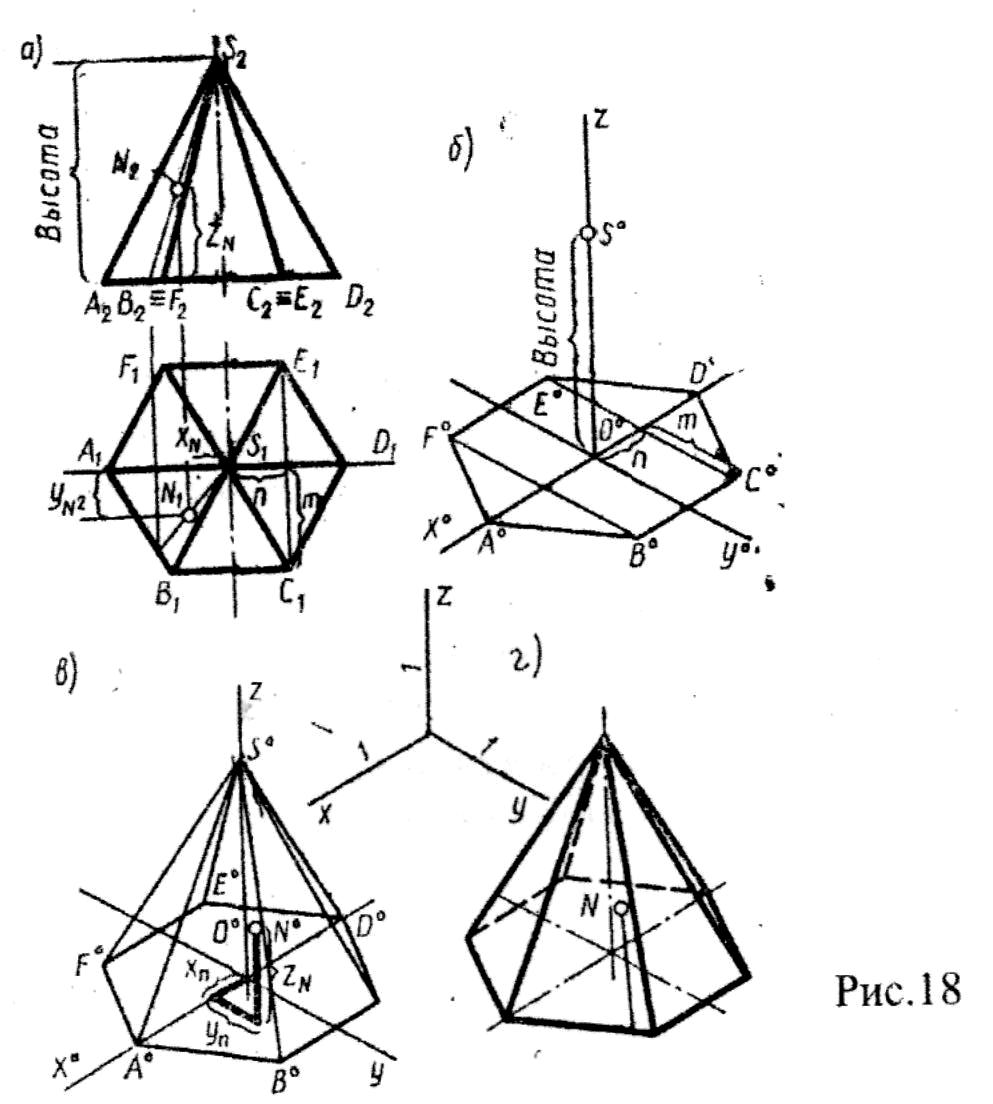
Построение проекций пирамиды начинается с построения основания, горизонтальная проекция которого представляет собой многоугольник. Фронтальная проекция основания изображается отрезком прямой. Из горизонтальной проекции вершины пирамиды проводят вертикальную линию связи, на которой от фронтальной проекции основания, отрезка прямой, перпендикулярно вверх откладывают высоту пирамиды и получают фронтальную проекцию вершины. Соединяя фронтальные проекции вершины пирамиды а вершин основания, получают фронтальные проекции ребер пирамиды. Горизонтальные проекции ребер получают, соединяя горизонтальную проекцию вершины с горизонтальными проекциями вершин основания. Профильную проекцию выполняют при помощи пиний связи (рис 13).

Поскольку грани многоугольников принято считать непрозрачными, то проекции некоторых ребер и граней будут невидимыми. Невидимые ребра определяют при помощи конкурирующих точек и показывают штриховыми линиями. Очерк многоугольника всегда будет видимым.

Построение проекций прямого кругового цилиндра начинают с изображения основания цилиндра. На горизонтальную плоскость оно проецируется без искажения (в виде окружности). Фронтальная проекция окружности представляет собой отрезок горизонтальной прямой, равный диаметру окружности основания. После построения основания на фронтальной проекции проводят две очерковые (крайние) образующие и на них откладывают высоту цилиндра. Проводят отрезок горизонтальной прямой, который является фронтальной проекцией верхнего основания цилиндра. Профильную проекцию строят при помощи линий связи (рис 14).

Построение проекций прямого кругового конуса начинают с построения горизонтальной проекции основания - окружности. Фронтальной проекцией основания является отрезок прямой, равный диаметру этой окружности. На фронтальной проекции из середины основания восстанавливают перпендикуляр и на нем откладывают высоту конуса. Полученную фронтальную проекцию вершины конуса соединяют прямыми с концами фронтальной проекции основания и получают фронталыгую проекцию конуса. Фронтальные и профильные проекции конуса одинаковы. То же можно сказать и о проекциях цилиндра (рис 15).

Шар проецируется на любую плоскость в окружность диаметра, равного диаметру шара (рис.16)

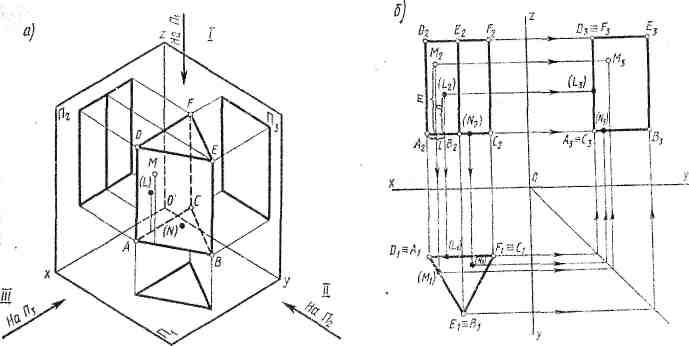
Рис. 12

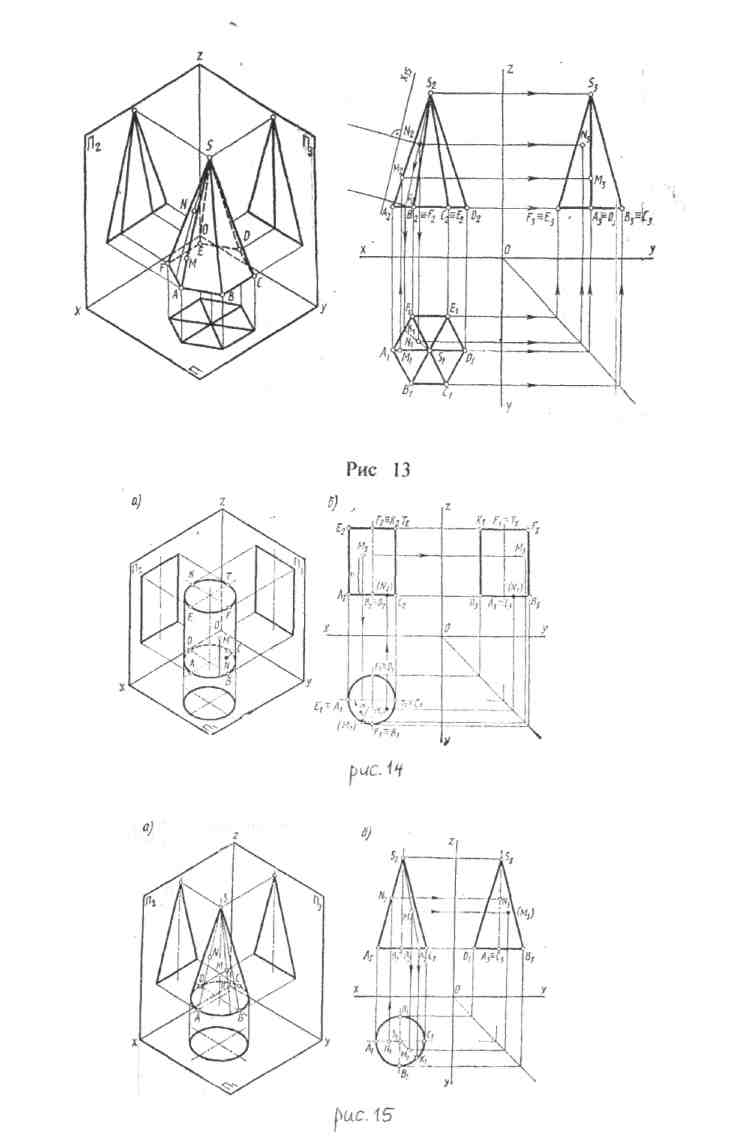
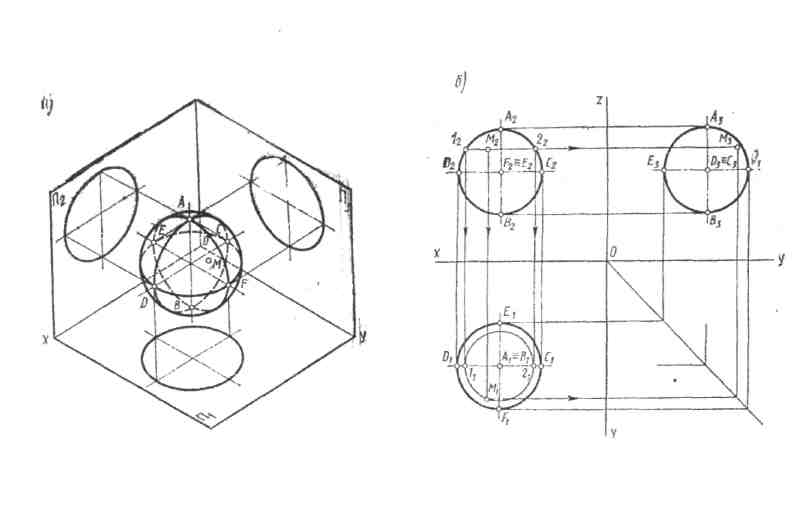
Рис.16

Основные теоретические сведения по теме «Аксонометрические проекции»

В технической графике особую группу составляют проекции, которые, получены путем параллельного проецирования предмета вместе с осями X, V, 7. пространственной системы прямоугольных координат на произвольную плоскость -аксонометрические проекции. В зависимости от направления проецирования по отношению к плоскости проекций аксонометрические проекции могут быть как прямоугольные, так и косоугольные.

Аксонометрические проекции относят к числу наглядных изображений. По ним можно легко получить общее представление о внешней форме предмета. Обычно предмет располагают так, чтобы на аксонометрической проекции были видны три стороны: верхняя, передняя и левая.

В зависимости от наклона осей координат к аксонометрической плоскости проекции делятся на: изометрические и диметрические.

Чаще всего используют прямоугольную изометрию и косоугольную диметрию. Правила построения изометрической и диметрической проекций одинаковы. Разница заключается в расположении осей и в длине отрезков, откладываемых вдоль оси Y.

Прямоугольную изометрию призмы выполняют в следующей последовательности. Вначале строят проекцию нижнего основания призмы по координатам вершин основания. Далее строят ребра и, отложив на этих прямых высоту призмы, получаем изометрию точек вершин другого основания призмы. Соединив эти точки прямыми, получим изометрическую проекцию призмы. В заключение отделяем видимые линии от невидимых; невидимые надо проводить штриховыми линиями

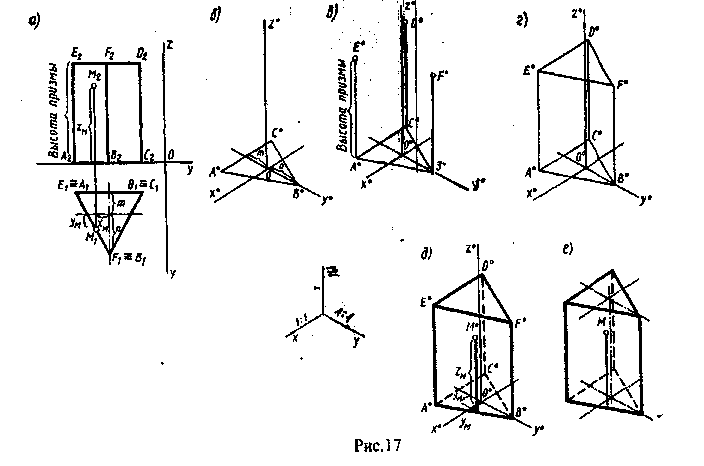
Изометрическую проекцию правильной пирамиды строят в той же последовательности, т.е. строят основание и откладывают высоту перпендикулярно основанию, а через вершину пирамиды проводят ребра (рис 18)

Изометрическую проекцию прямого кругового цилиндра начинают с построения аксонометрической проекции основания - овала. Далее через центр овала проводим осевую линию цилиндра и на ней от центра основания откладываем высоту цилиндра и строим верхнее основание цилиндра в виде овала. К полученным двум основаниям цилиндра проводим крайние образующие, касательные к основаниям (они параллельны оси цилиндра) (рис. 19)

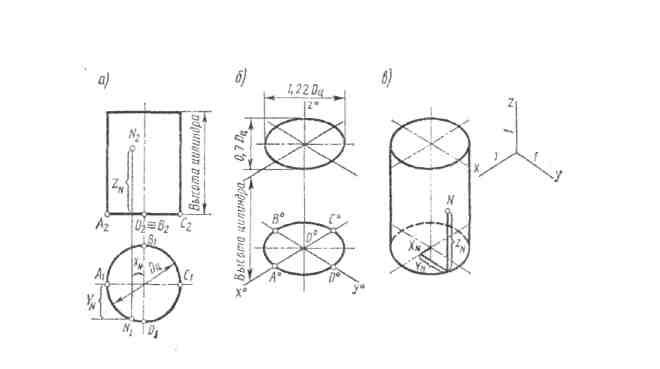
Рис.19

Изометрическую проекцию конуса начинают с построения аксонометрической проекции основания - овала. Далее через центр овала проводим осевую линию конуса и на ней от центра основания откладываем высоту конуса. Соединяем вершину конуса с основанием двумя касательными (рис. 20)

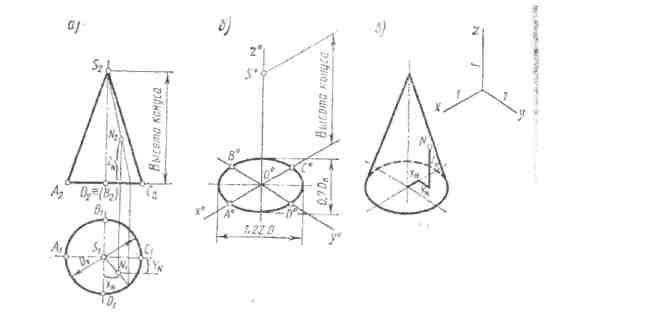
Рис. 20

Изометрия шара выполняется следующим образом: из намеченного центра проводят окружность заданного диаметра шара Строим прямоугольную изометрию экватора. Проводим окружность, касательную к овалу, - очерковую окружность шара. Далее строим прямоугольную изометрию фронтального и профильного меридианов. Очерковую окружность, видимые части экватора, фронтального и профильного меридианов обводим сплошной основной линией (рис.21). Невидимые части экватора и меридианов можно не показывать для ясности.

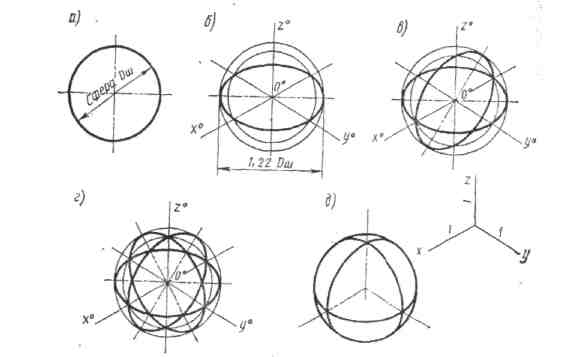
Рис. 21

На рисунке 22 приведены примеры построения овалов, расположенных в плоскостях параллельных фронтальной и профильной плоскостям проекций.

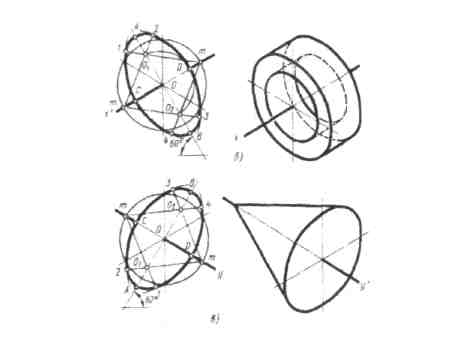
Рис. 22

Методические указания.

При выполнении графической работы необходимо проанализировать положение каждого тела по отношению плоскостей проекций и друг друга. Следует определить направление образующих данного тела и их положение относительна плоскостей проекций.

При построении аксонометрической проекции проработайте ГОСТ 2.317-69 и выберите ту аксонометрическую проекцию, которая даст наиболее наглядное представление о расположении всей группы тел.

Порядок выполнения.

1. Изучить методические указания, ГОСТы и соответствующую литературу.

2. Подготовить рабочее место, инструменты, бумагу и пособия.

3. Ознакомиться с содержанием индивидуального задания и образцом выполнения.

4. Разделить поле чертежа на 2 части. Наметить места расположения заданий.

5. Проанализировать группу геометрических тел. Определить, какие геометрические тела входят в ее состав.

6. Определить направление образующих данного тела и их положение относительно плоскостей проекций. Обратить внимание на тела вращения, определить их параллели и экватор.

7. В левой верхней части листа вычертить тонкими линиями условие задачи. Построить третью проекцию группы геометрических тел.

8. Нанести размеры.

9. Выбрать вид аксонометрической проекции и рациональный прием построения.

10. В правой нижней части листа вычертить аксонометрическое изображение группы геометрических тел.

11. Проверить правильность выполнения задания. Выполнить обводку.

12. Заполнить основную надпись.

Задание 5

«Сечение тела плоскостью»

Цель:

• изучить правила построения линии среза, получаемых в технических формах при пересечении тел плоскостями.

• научиться выполнять комплексный чертеж детали, представляющей собой сумму геометрических тел, усеченной, проецирующей плоскостью

• ознакомиться со способами преобразования проекций.

• научиться находить натуральную величину фигуры сечения.

• уметь выполнять аксонометрическую проекцию усеченного тела.
Содержание. Построить три проекции комбинированного тела. Построить сечение тела плоскостью и найти натуральную величину фигуры сечения. Выполнить аксонометрическую проекцию усеченного комбинированного тела. Графическую работу выполнить на листе чертежной бумаги формата А3(297х420). Образец выполнения дан на рис. 23. Варианты графической работы приведены в таблице 3.

Основные теоретические сведения по теме

«Пересечение геометрических тел проецирующими плоскостями»

Многие детали очень часто имеют формы, представляющие собой различные геометрические поверхности, рассеченные плоскостями.

Рассекая геометрическое тело плоскостью, получают сечение - плоскую фигуру, ограниченную линией, все точки которой принадлежат как секущей плоскости, так и поверхности тела.

Дата добавления: 2014-11-18