Основные теоретические сведения по теме

«Способы преобразования проекц ий»

Если фигура сечения геометрического тела ни на одну плоскость проекций не проецируется в натуральную величину, тогда истинную величину фигуры сечения находят способом замены плоскостей или способом вращения.

Сущность способа перемены плоскостей проекций состоит в том, что положение проецируемого объекта остается неизменным, а изменяют положение плоскостей проекций. Выбирается такое положение новой плоскости проекций, при котором геометрические фигуры будут располагаться по отношению к ней перпендикулярно или параллельно.

При преобразовании проекций способом вращения положение плоскостей проекций остается неизменным. Геометрическая фигура путем вращения вокруг прямой (оси вращения), расположенной параллельно или перпендикулярно плоскости проекций, переводится в частное положение (располагается параллельно или перпендикулярно плоскости проекций). При этом все точки геометрической фигуры вращаются в плоскостях, перпендикулярных оси вращения.

рис.31

Порядок выполнения.

1. Изучить рекомендованную литературу

2. Подготовить рабочее место, инструменты, бумагу и пособия.

3. Ознакомиться с содержанием индивидуального задания и образцом выполнения.

4. Проанализировать из каких геометрических тел состоит данный предмет, и какие секущие плоскости дают линию среза.

5. Вычертить тонкими линиями условие задачи

6. Построить третью проекцию комбинированного тела

7. Определить, на каких проекциях следует построить линии сечения

8. Определить характерные и промежуточные точки линий сечения

9. Соединить полученные точки

10.Построить действительную фигуру сечения

11 Вычертить аксонометрическую проекцию усеченного комбинированного тела

12.Проверить правильность выполнения задания. Выполнить обводку.

13.Заполнить основную надпись.

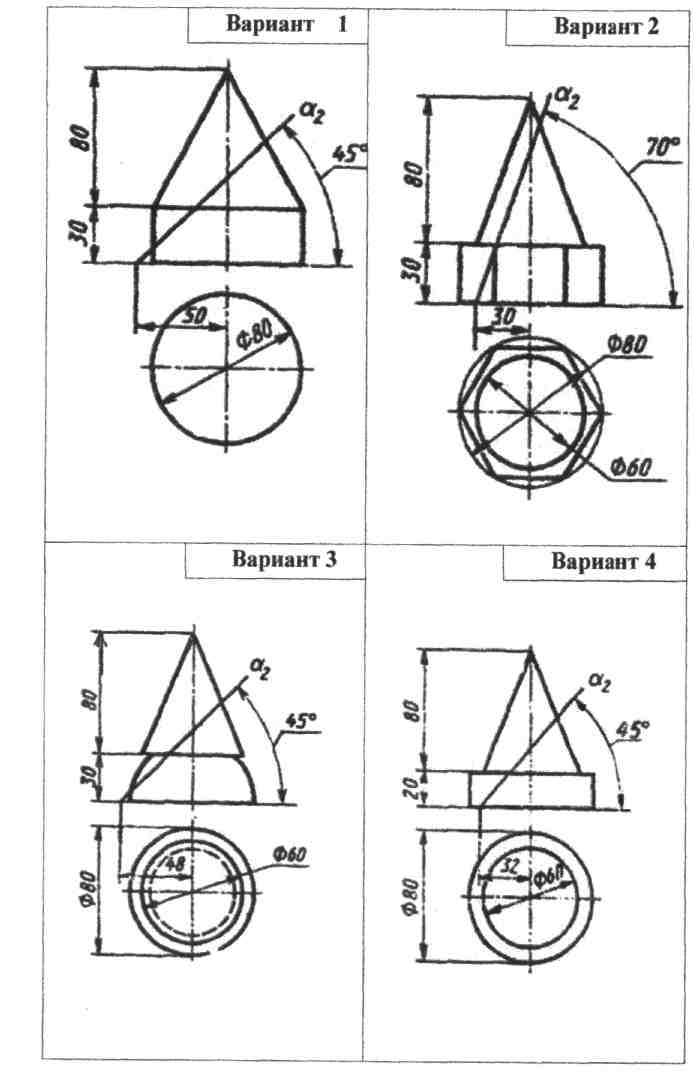
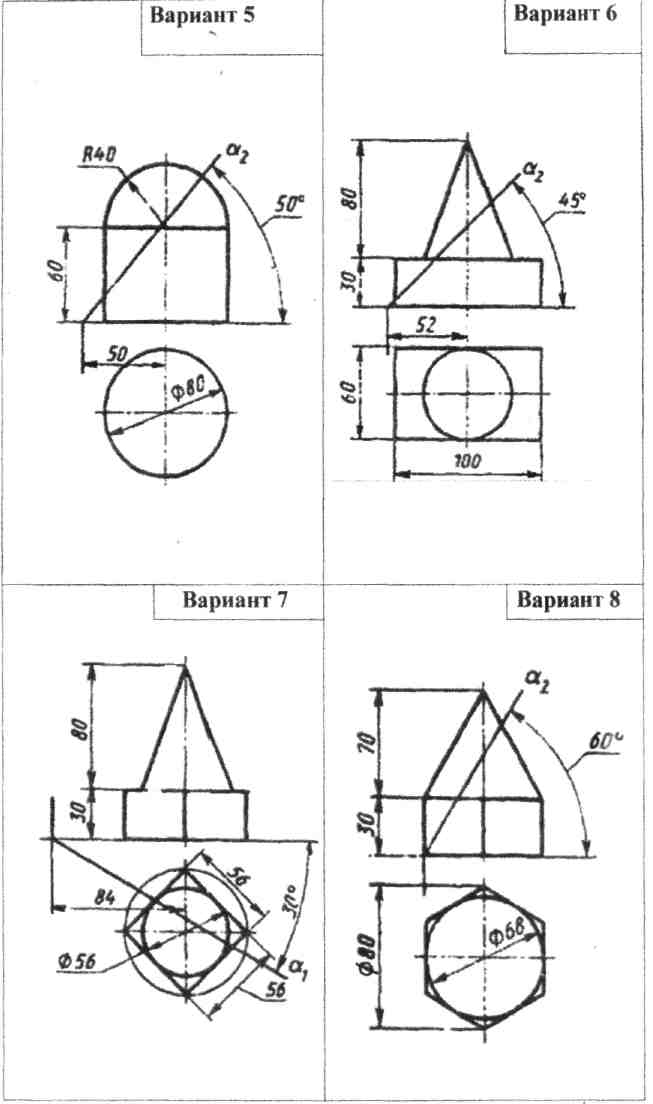
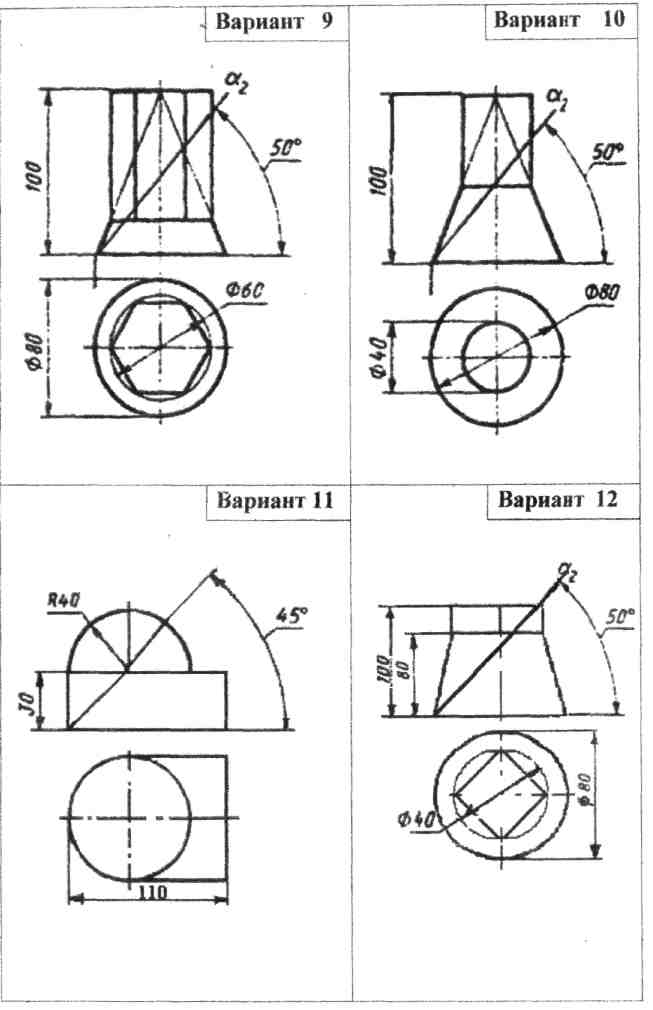
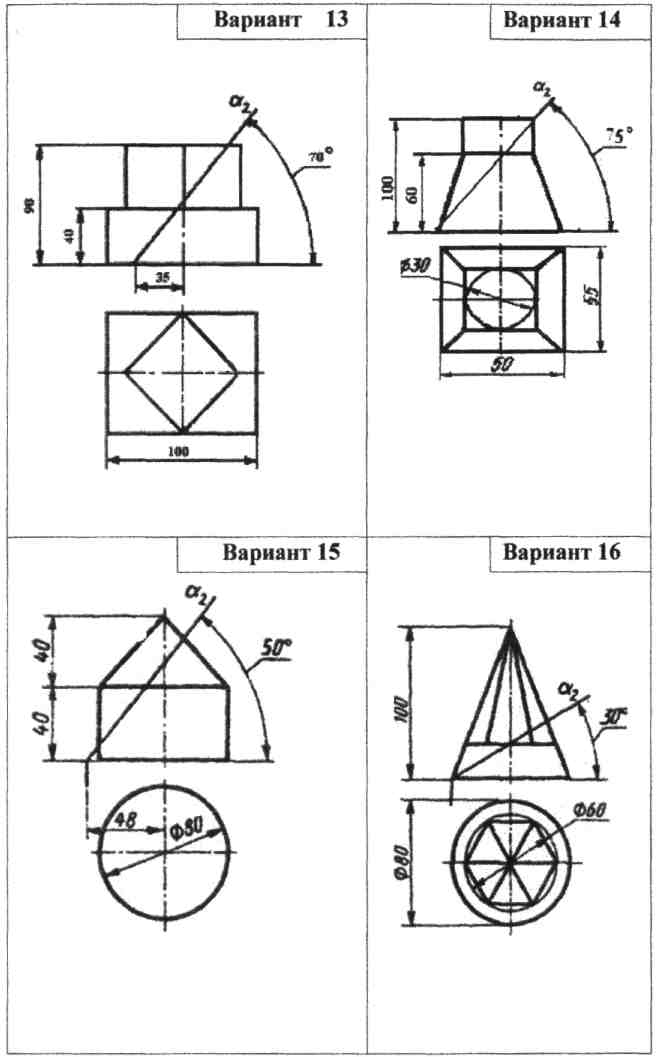
Задание 6

«Взаимное пересечение поверхностей геометрических тел»

Цель:

• изучить способы построения линий взаимного пересечения поверхностей (линии перехода) в технических формах.

• научиться выполнять чертеж детали с построением линий взаимного пересечения поверхностей.

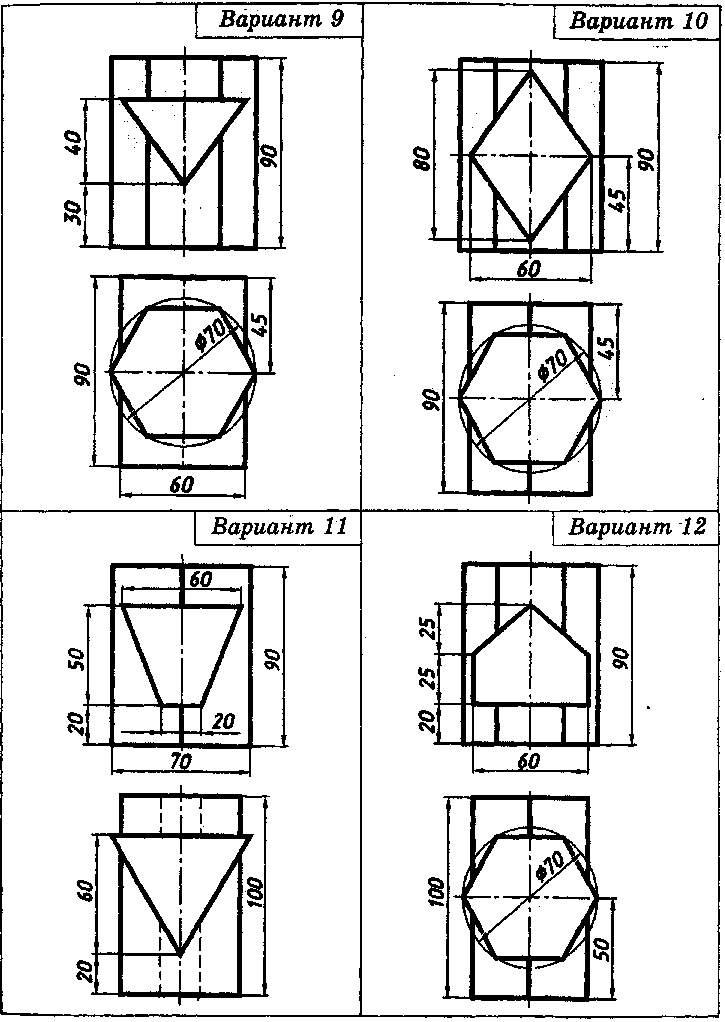
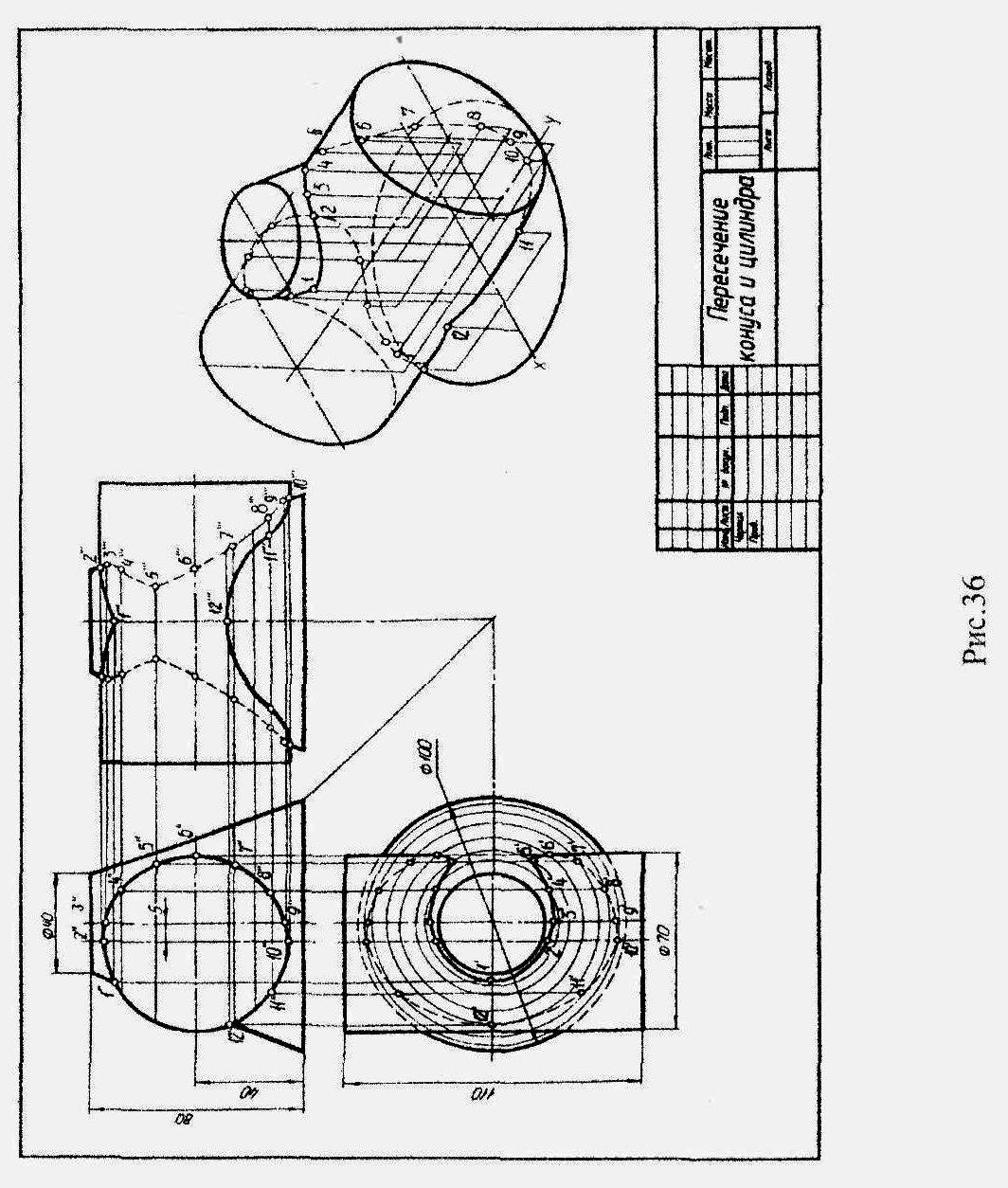
Содержание. На листе чертежной бумаги формата А3(297х420) по двум заданным проекциям геометрических тел вычертить профильную проекцию. Построить проекции линии пересечения поверхностей геометрических тел, определить видимость. Выполнить аксонометрическую проекцию. Нанести размеры. Образец выполнения дан на рис.36. Варианты графической работы приведены в таблице 4.

Основные теоретические сведения по теме

«Взаимное пересечение поверхностей геометрических тел»

Многие технические детали представляют собой комбинацию геометрических тел, поверхности которых могут пересекаться. При пересечении поверхностей геометрических тел образуется линия пересечения, все точки которой принадлежат обеим поверхностям.

Построение проекций линии пересечения сводится к нахождению ряда общих точек для обеих поверхностей. Общим способом построения проекций линии пересечения двух поверхностей является способ вспомогательных секущих поверхностей. В качестве вспомогательных поверхностей обычно используют плоскости или сферы.

Но в ряде частных случаев проекции линии пересечения двух поверхностей можно построить, не используя способа вспомогательных секущих поверхностей. Это становиться возможным тогда, когда одна или обе из пересекающихся поверхностей являются проецирующими.

I. Если обе пересекающиеся поверхности являются проецирующими, то две проекции линии пересечения будут совпадать, с вырожденными проекциями поверхностей. (рис. 32а. б. в)

К проецирующим поверхностям относятся:

· цилиндрическая поверхность

· призматическая поверхность I

Решение задачи в этом случае сводится к построению по двум имеющимся проекциям отдельных точек линии пересечения их третей проекции.

2. Если одна из пересекающихся поверхностей является проецирующей, то одна из проекций линии пересечения будет совпадать с вырожденной проекцией этой проецирующей поверхности. Остальные проекции линии пересечения строят по точкам, выбранным на имеющейся проекции линии пересечения, исходя из условия принадлежности этих точек непроецирующей поверхности. (рис.33 а, б,.в)

К непроецирующим поверхностям относятся:

• сферическая поверхность

• коническая поверхность

• пирамидальная поверхность

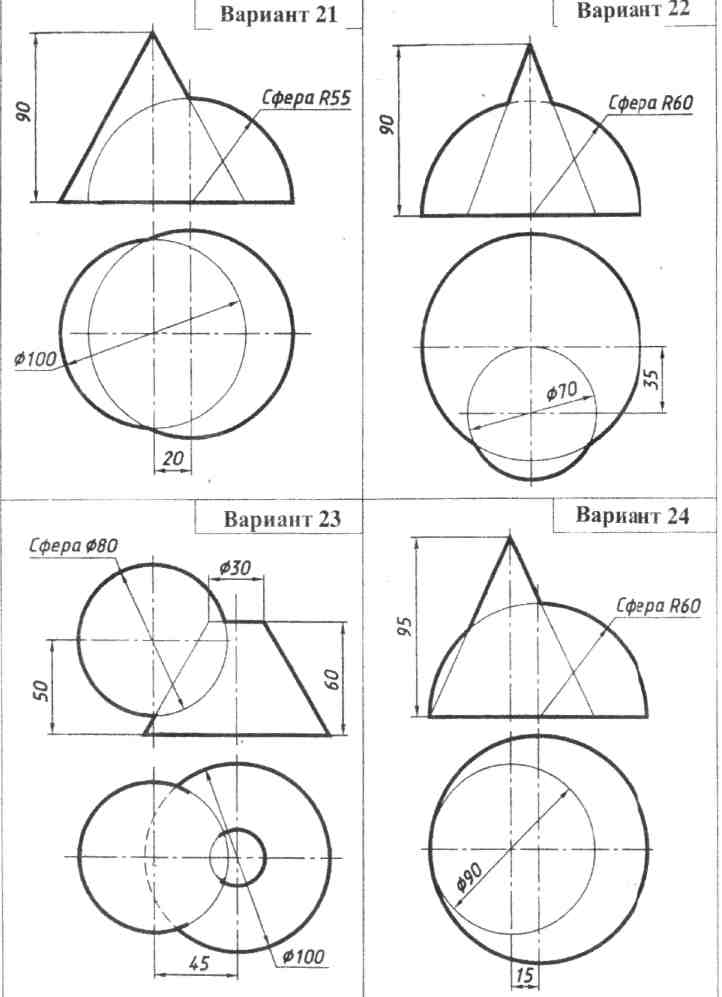
3. Если обе пересекающиеся поверхности являются непроецирующими, то построение проекций линии пересечения поверхностей выполняют методом вспомогательных секущих плоскостей или методом вспомогательных секущих сфер (рис.34).

рис.34

Вспомогательные сферические поверхности можно использовать лишь при следующих условиях:

· пересекающиеся поверхности должны быть поверхностями вращения

· оси поверхностей вращения должны пересекаться;

· точка пересечения осей является центром вспомогательных сфер

· оси поверхностей вращения должны быть параллельны какой-либо плоскости проекций

Примеры применения вспомогательных сферических поверхностей показаны на рис. 35а и б.

Рис. 35

а) б)

рис.35

На рис. 35а дано построение фронтальных проекций линии пересечения поверхностей двух цилиндров, оси которых пересекаются под острым углом.

Вспомогательные сферические поверхности проводят из точки О' пресечения осей цилиндров.

Построим, например, фронтальную проекцию некоторой промежуточной точки линии пересечения. Для этого из точки О' проводят сферическую поверхность радиуса R, которая на данной проекции изобразится в виде окружности этого же радиуса. Окружность радиуса R пересечет горизонтальный цилиндр по окружностям диаметра СО, а наклонно расположенный цилиндр - по окружностям диаметра АВ.

В пересечении полученных проекций окружностей - отрезков а' b' и с' d" - находят проекцию 2' промежуточной точки линии пересечения.

Пределы радиусов сферических поверхностей находят следующим образом: наибольшая окружность сферической поверхности должна пересекаться с контурными образующими I — I и II- II цилиндра и наименьшая должна быть касательной к одной из данных пересекающихся поверхностей и пересекаться с образующими другой поверхности.

Методические указания.

При решении задач на построение проекции линии пересечения поверхностей двух геометрических тел следует придерживаться следующей последовательности:

1. По условию предложенной задачи необходимо установить, какие геометрические тела пересекаются и как располагаются их пересекающиеся поверхности относительно плоскостей проекций.

2. Выявить наличие проецирующих поверхностей и выделить на чертеже их вырожденные проекции

3. Выбрать рациональный способ построения проекций точек линии пересечения

4. Построить проекции линии пересечения поверхностей, учитывая следующие рекомендации:

• при пересечении поверхностей вращения образуется чаще всего пространственная линия пересечения, а в отдельных случаях - плоская кривая линия. При построении проекций линии пересечения поверхностей вращения вначале нужно выявить наличие характерных точек (высших, низших, точек, разделяющих видимые участки проекций линии пересечения, точек пересечения очерков и т.д.), построить их.

Наметить необходимое количество промежуточных точек, построить их проекции выбранным способом. Их количество должно быть минимальным, но достаточно для выявления характера кривизны линии пересечения.

• в случаях пересечения поверхностей многогранников линия пересечения будет представлять собой ломаную линию. Для построения проекции точек ее излома необходимо определить точки пересечения ребер одного многогранника с гранями другого.

• при пересечении поверхностей вращения и многогранника линия пересечения будет состоять их плоских кривых линий. Характерными точками здесь будут точки пересечения ребер многогранников с поверхностями вращения. Необходимо также наметить и построить проекции ряда промежуточных точек.

5. Установить последовательность соединения построенных проекций точек линии пересечения.

6. Решить вопрос о видимости отдельных участков линии пересечения. При этом следует руководствоваться следующими соображениями: участки линии пересечения будут видимы в том случае, когда они расположены на видимых частях обеих поверхностей

7. Соединить последовательно построенные точки линии пересечения плавной кривой линией (для поверхностей вращения) или ломаной линией (для поверхностей многогранников).

8. Рассмотреть вопрос о наличии и видимости сохранившихся на чертеже очерков (ребер) геометрических тел.

9. В аксонометрической проекции точки линии пересечения поверхностей могут быть построены по их координатам.

Порядок выполнения.

1. Изучить основные теоретические сведения, методические указания и рекомендованную литературу

2. Подготовить рабочее место, инструменты, бумагу и пособия.

3. Ознакомиться с содержанием индивидуального задания и образцом выполнения.

4. Вычертить тонкими линиями условие задачи.

5. Построить проекции линии пересечения,

6. Нанести размерные линии и размерные числа.

7. Построить аксонометрическую проекцию.

8. Обвести чертеж.

9. Заполнить основную надпись.

Учебное издание

Рылова О.Г, Селях Т.П.

Дата добавления: 2014-11-18