Урок № 5

Тема: Показникова форма комплексного числа.

План:

1. Показникова форма комплексного числа.

2. Дії над комплексними числами в показникові формі.

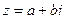Кожному комплексному числу можна поставити у відповідність точку координатної площини з координатами (а,b). Таким чином встановлюється взаємно однозначна відповідність між комплексними числами і точками координатної площини. Зображається комплексне число у вигляді вектора, початок якого співпадає з початком координат, а кінець знаходиться в точці (а,b).

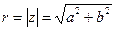
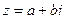
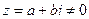Означення: Модулем комплексного числа називається довжина вектора, що зображає дане комплексне число:.

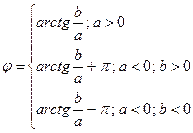
Означення: Аргументом комплексного числа називається кут між додатнім напрямком осі Ох і вектором, що зображає дане комплексне число:

Будь-яке комплексне число можна записати у вигляді, який називається тригонометричною формою комплексного числа: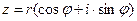

Можна показати, що вирази та 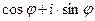мають одну і ту саму суть. Запис 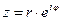називається показниковою формою комплексного числа. Додавання та віднімання комплексних чисел в показниковій формі як правило не виконується або виконується геометрично.

Для того щоб помножити два комплексних числа в показниковій формі треба помножити модулі і додати аргументи.

Для того щоб поділити два комплексних числа в показниковій формі треба поділити модулі і відняти аргументи.

Для того щоб піднести комплексне число в показниковій формі до степеню треба до цього степеню піднести модуль і домножити аргумент на показник степеню.

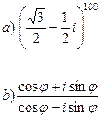
Добування кореня n-го степеню з комплексного числа в показниковій формі здійснюється за формулою:, де k приймає значення від 0 до n-1.

Приклади. Виконати дії в показниковій формі:

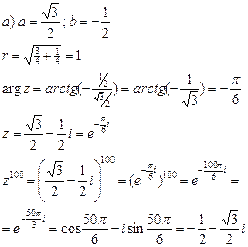
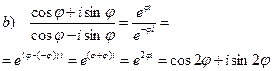
Завдання. Виконати дії в показниковій формі:

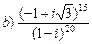
Контрольні запитання:

1. Що називають модулем комплексного числа?

2. Дати означення аргумента комплексного числа.

3. Записати тригонометричну і показникову форму комплексного числа.

4. Як виконати дії з комплексними числами в показниковій формі?

Література: [1] - § 16

Дата добавления: 2014-11-18