Урок № 15

Тема: Теореми про середнє. Формула Тейлора.

План:

1. Основні теореми диференціального числення

2. Формула Тейлора

Теорема Ферма. Якщо диференційовна на проміжку 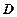функція 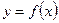досягає найбільшого або найменшого значення у внутрішній точці цього проміжку, то похідна функції в цій точці дорівнює нулю, тобто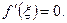

Припустимо, для визначеності, що набуває в точці найбільшого значення, тобто для всіх .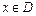

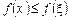За означенням похідної , причому ця границя не залежить від того, як наближається 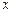до — справа чи зліва.

Розглянемо відношення .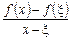

Для всіх х, достатньо близьких до точки 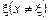, маємо:

Перейдемо в останніх нерівностях до границі при . Дістанемо

.

Аналогічно розглядається випадок, коли функція 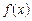набуває в точці найменшого значення.

Геометричний зміст теореми Ферма. Геометричний зміст похідної 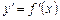являє собою кутовий коефіцієнт дотичної до кривої 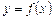. Звідси рівність нулю похідної 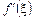геометрично означає, що у відповідній точці цієї кривої дотична паралельна осі Ох.

Теорема Ролля. Якщо функція f(х): 1) неперервна на сегменті [a; b]; 2) диференційовна на інтервалі (а; b); 3) на кінцях сегмента набуває рівних між собою значень, тобто f(a) = f(b), то на інтервалі (а; b) існує хоча б одна точка 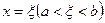, для якої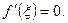

Геометричний зміст теореми Ролля. Якщо крайні ординати неперервної кривої у = f (х), яка має в кожній точці дотичну, рівні, то на цій кривій знайдеться принаймні одна точка з абсцисою , в якій дотична паралельна осі Ох (рис. 1).

Рис. 1

Теорема Лагранжа (теорема про скінченні прирости функції).

Якщо функція f(х): 1) неперервна на сегменті [a; b]; 2) диференційовна на інтервалі (а; b), то на інтервалі знайдеться хоча б одна точка 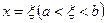, така що

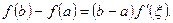(1)

Геометричний зміст теореми Лагранжа. Запишемо формулу (1) у вигляді

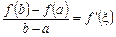. (2)

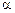З рис. 2 бачимо, що величина є тангенсом кута нахилу хорди, що проходить через точки А і В графіка функції у = f (х) з абсцисами а і b.

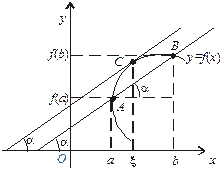
Рис. 2

Водночас, — тангенс кута нахилу дотичної до кривої у точці С з абсцисою . Таким чином, геометричний зміст рівності (1) або рівносильної для неї рівності (2) можна визначити так: якщо для всіх точок кривої у = f (х) існує дотична, то на цій кривій знайдеться точка з абсцисою , в якій дотична паралельна хорді АВ, що сполучає точки А і В.

Теорема Коші. Якщо f(x) і 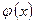дві функції: 1) неперервні на сегменті [a; b]; 2) диференційовні на інтервалі (а; b); 3) 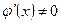для , то на інтервалі (а; b) знайдеться хоча б одна точка 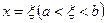, така що

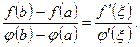
Формула Тейлора. Нехай задано многочлен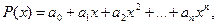

де 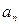- довільні дійсні числа, які називаються коефіцієнтами многочлена.

Виразимо коефіцієнти даного многочлена через значення многочлена 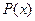та його похідні.

З цією метою будемо послідовно диференціювати многочлен. Матимемо:

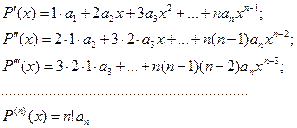
Отримуємо

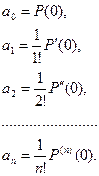
Тоді многочлен 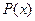можна записати так:

Дану формулу називають формулою Тейлора для многочлена.

Візьмемо довільну функцію 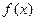, яка в околі деякої точки і в самій точці має похідні до n -го порядку включно.

Тоді для такої функції можна побудувати многочлен:

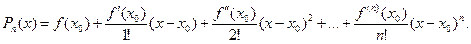
Цей многочлен називається многочленом Тейлора для функції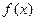

Приклад 1. Чи буде виконуватися теорема Ролля для функції , якщо а = 1, b = 5? При якому значенні ?

l Оскільки функція f (x) неперервна та диференційовна на всій числовій прямій і значення функції f (x) на границях сегмента [1, 5] рівні між собою f (1) = f (5) = 95, то теорема Ролля буде виконуватись на інтервалі (1, 5). Значення визначаємо з рівняння , тобто .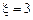

Приклад 2. Знайти координати точки М на дузі АВ кривої , в якій дотична паралельна хорді АВ, якщо А (1; 1) та В (3; –3).

l Функція неперервна та диференційовна при всіх значеннях х. За теоремою Лагранжа між двома значеннями а = 1 та b = 3 існує значення 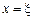, яке задовольняє рівності , де . Підставимо дані умови задачі: 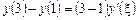, тобто 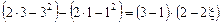. Звідки 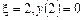. Таким чином, точка М має координати (2; 0).

Завдання

1. Чи буде виконуватися теорема Ролля для функції 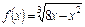на інтервалі (0; 8)? При якому значенні ?

2. Показати, що похідна многочлена 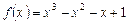має дійсний корінь на інтервалі (–1; 1).

3. В якій точці дуги АВ кривої 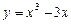дотична паралельна хорді АВ, якщо А (0; 0), В (3; 18)?

Контрольні запитання:

1. Сформулюйте Теорему Ферма.

2. В чому полягає геометричний зміст теореми Ферма?

3. В чому полягає геометричний зміст теореми Ролля? Покажіть на рис.

4. В чому полягає геометричний зміст теореми Лагранжа?

5. В чому полягає формула Тейлора?

Література: [11], Р.7, п.7.1, 7.3.

[18] – с.155-164.

Дата добавления: 2014-11-18