
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Урок № 52
|
|
|
|
Контрольні запитання.
1. Дати означення вектора.
2. Які лінійні операції можна виконувати над векторами?
3. Сформулювати ознаки паралельності і перпендикулярності векторів.
4. Дати поняття векторного базису.
5. Як виконати операції над векторами в координатах?
Література: [1] - § 4-9
Тема: Загальне рівняння прямої. Взаємне розміщення двох прямих. Відстані від точки до прямої.
План:
1. Загальне рівняння прямої.
2. Взаємне розміщення двох прямих.
3. Відстань від точки до прямої.
Нехай пряма l задана рівнянням 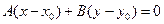 . Виконаємо тотожні перетворення:
. Виконаємо тотожні перетворення:
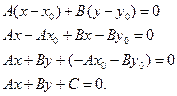
Одержане рівняння називається загальним рівнянням прямої.
Нехай А =0, тоді 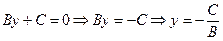 . Позначимо
. Позначимо 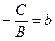 , одержимо y=b – рівняння прямої, паралельної осі Ох.
, одержимо y=b – рівняння прямої, паралельної осі Ох.
Нехай В =0, тоді  . Позначимо
. Позначимо  , одержимо x=a – рівняння прямої, паралельної осі Оу.
, одержимо x=a – рівняння прямої, паралельної осі Оу.
 Нехай
Нехай 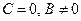 , тоді
, тоді 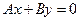 , або
, або 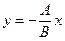 . Покладемо
. Покладемо 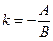 , одержимо
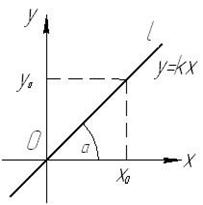
, одержимо 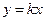 . Пряма проходить через початок координат. Нехай
. Пряма проходить через початок координат. Нехай 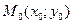 довільна точка прямої l. Тоді
довільна точка прямої l. Тоді 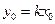 , або
, або 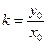 . З малюнка видно, що
. З малюнка видно, що 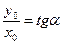 .
.
Означення 1. Тангенс кута нахилу прямої до додатного напрямку осі Ох називається кутовим коефіцієнтом прямої.
Нехай 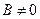 , тоді
, тоді 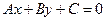 , або
, або 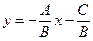 . Покладемо
. Покладемо 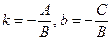 , одержимо
, одержимо  .
.
Означення 2. Число b називається початковою ординатою прямої, а рівняння  - рівнянням прямої з кутовим коефіцієнтом.
- рівнянням прямої з кутовим коефіцієнтом.
Зауваження. Кутовий коефіцієнт прямої, яка паралельна осі Оу, не існує.
Нехай на площині задано дві прямі: 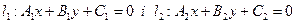 .
.
Нехай 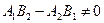 , або
, або 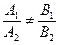 при
при 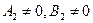 . Тоді
. Тоді 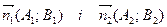 - не колінеарні. Отже
- не колінеарні. Отже 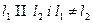 , тоді
, тоді 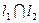 .
.
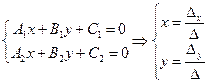 - точка перетину прямих.
- точка перетину прямих.
Нехай 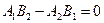 , або
, або  при
при 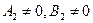 . Тоді
. Тоді 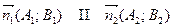 . Отже прямі або паралельні, або співпадають.
. Отже прямі або паралельні, або співпадають.
Нехай 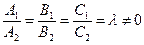 при
при 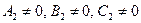 . В цьому випадку
. В цьому випадку 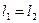 .
.
Нехай 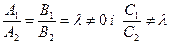 при
при 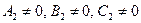 . В цьому випадку
. В цьому випадку 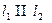 .
.
Теорема 1. Прямі 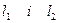 паралельні між собою тоді і тільки тоді, коли їх кутові коефіцієнти рівні.
паралельні між собою тоді і тільки тоді, коли їх кутові коефіцієнти рівні.
Теорема 2. Прямі 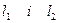 перпендикулярні між собою тоді і тільки тоді, коли їх кутові коефіцієнти обернені по величині і протилежні по знаку.
перпендикулярні між собою тоді і тільки тоді, коли їх кутові коефіцієнти обернені по величині і протилежні по знаку.
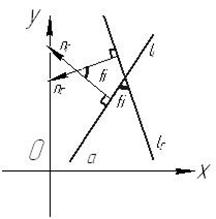 Нехай треба обчислити кут між прямими
Нехай треба обчислити кут між прямими 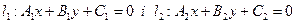 . З малюнка видно, що кут між прямими дорівнює куту між нормальними векторами цих прямих. Тому
. З малюнка видно, що кут між прямими дорівнює куту між нормальними векторами цих прямих. Тому 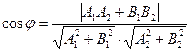 .
.
Відстань між точкою 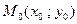 і прямою
і прямою 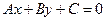 обчислюється за формулою
обчислюється за формулою 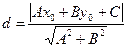 .
.
Приклади. 1. Пряма задана параметричним рівнянням 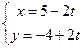 . Записати загальне рівняння цієї прямої.
. Записати загальне рівняння цієї прямої.

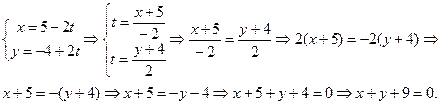
2. Знайти точку перетину прямих 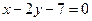 та
та 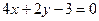 .
.
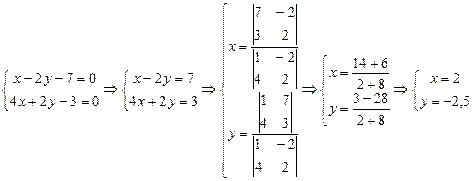 .
.
3. При якому значенні а прямі 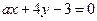 та
та  паралельні.
паралельні.
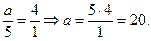
4. Знайти кут між прямими 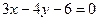 та
та  .
.
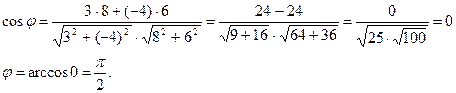
Прямі перпендикулярні.
5. Координати вершин трикутника А(2;-3), В(0;1) і С(-1;-1). Обчислити довжину висоти проведеної з вершини А на сторону ВС.
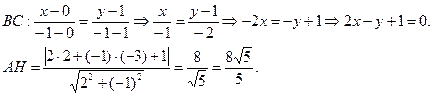
Завдання: 1. Пряма задана канонічним рівнянням 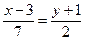 . Записати загальне рівняння цієї прямої.
. Записати загальне рівняння цієї прямої.
2. Знайти точку перетину прямих 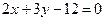 та
та 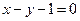 .
.
3. При якому значенні а прямі 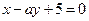 та
та 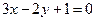 паралельні.
паралельні.
4. Знайти кут між прямими 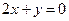 та
та 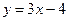 .
.
5. Координати вершин трикутника А(2;-3), В(0;1) і С(-1;-1). Обчислити довжину висоти проведеної з вершини С на сторону ВА.
|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 407; Нарушение авторских прав?; Мы поможем в написании вашей работы!