Приклад 1. Монету підкидають один раз. (Тут і далі припускаємо, що падає монета на рівну і тверду підлогу.) Поява герба (цифри) — подія випадкова

Урок №62

Тема: Випадкові події та їх ймовірності. Теореми додавання і множення ймовірностей.

План

1. Випадкові події. Ймовірність випадкової події

2. Теореми додавання.

3. Теорема множення для незалежних подій.

Подія називається випадковою, якщо за певного комплексу умов у результаті експерименту вона може настати або не настати залежно від дії численних дрібних факторів, урахувати які дослідник не в змозі.

Випадкові події позначають символами А, В, С, … або А ₁, А ₂, А ₃,…, А_k; В ₁, В ₂, …, В_n.

Отже, випадкові події пов’язані експериментами, наслідки яких є неоднозначними.

Подія, що може відбутися внаслідок проведення однієї і лише однієї спроби (експерименту), називається простою (елементарною) випадковою подією.

Елементарні події позначаються w _і (і = 1, 2, 3,…) і в теорії ймовірностей, так само як, скажімо, точка в геометрії, не поділяються на простіші складові.

Приклад 2. Монету підкидають один раз. Визначити елементарні події цього експерименту.

Розв’язання. Можливі такі елементарні випадкові події:

w₁ = г (монета випаде гербом);

w₂ = ц (монета випаде цифрою).

Означення. Імовірністю випадкової події А називається невід’ємне число Р (А), що дорівнює відношенню числа елементарних подій m (0 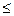m 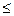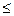n), які сприяють появі А, до кількості всіх елементарних подій n простору Ω:

Р (А) = .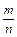

Для неможливої події Р (Æ) = 0 (m = 0);

Для вірогідної події Р (Ω) = 1 (m = n).

Отже, для довільної випадкової події

.

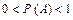Приклад 3. У ящику міститься 15 однотипних деталей, із яких 6 бракованих, а решта — стандартні. Навмання з ящика береться одна деталь. Яка ймовірність того, що вона буде стандартною?

Розв’язання. Число всіх рівноможливих елементарних подій для цього експерименту: n = 15. Нехай А — подія, що полягає в появі стандартної деталі. Число елементарних подій, що сприяють появі випадкової події А, дорівнює дев’яти (m = 9). Маємо: .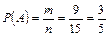

Теорема 1. (додавання для несумісних подій): Ймовірність появи однієї з двох випадкових несумісних подій дорівнює сумі їх ймовірностей:

Дане твердження справджується і для n випадкових подій.

Теорема 2. (додавання для сумісних подій): Якщо випадкові події А та В сумісні, то ймовірність їх об’єднання дорівнює сумі їх ймовірностей без ймовірності їх сумісної появи:

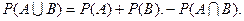
Дане твердження також справджується і для n випадкових подій.

Приклад 4. В урні знаходиться 30 кульок: 10 червоних і 15 білих, 5 синіх. Навмання витягуємо одну кульку. Знайти ймовірність того, що вона буде кольоровою.

Розв’язання. Поява кольорової кульки означає появу або червоної, або синьої кулі. Ймовірність появи червоної кулі (подія А):

Р(А) = .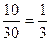

Ймовірність появи синьої кулі (подія В):

Р(В) = .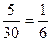

Події А та В несумісні (поява кулі одного кольору виключає появу кулі іншого кольору), тому застосовуємо теорему додавання ймовірностей для несумісних подій:

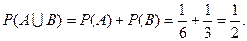
Теорема 3. (множення для незалежних подій): Ймовірність сумісної появи двох подій дорівнює добутку ймовірностей першої та другої події.

Р(А 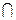В)=Р(А)×Р(В).

Завдання.

1. Гральний кубик підкидають один раз. Яка ймовірність того, що на грані кубика з’явиться число, кратне 3?

2. Задано множину цілих чисел 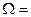{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16, 17,18,19,20,21,22,23,24,25,26,27,28,29,30}. Навмання з цієї множини беруть одне число. Знайти ймовірність того, що воно виявиться кратним 5 або 7

Дата добавления: 2014-11-18