Урок №66

Контрольні запитання.

1. Опишіть схему Бернуллі. Які елементарні події повторюються в цих дослідах?

2. Запишіть формулу Бернуллі.

3. Який закон розподілу називається біномним?

4. Монету підкидають 8 разів. Яка ймовірність того, що орел випаде зверху 5 разів?

5. У сім’ї троє дітей. Визначте ймовірність того, що серед них два хлопчики, якщо ймовірності народження хлопчика і дівчинки однакові?

Література: [1] – Розділ 11.

Тема: Дискретні випадкові величини. Поняття про закон розподілу.

План

1. Дискретні випадкові величини. Приклад.

2. Закон розподілу випадкової величини.

Означення 1. Якщо множина можливих значень випадкової величини є зчисленною то таку величину називають дискретною. У противному разі її називають неперервною.

Приклад 1. Задано множину цілих чисел Ώ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Навмання беруть одне число. Елементарними подіями будуть такі: поява одного з чисел 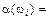1, 2, 3, …,10 з певною ймовірністю. Множина можливих значень є дискретною, а тому й випадкова величина — поява одного з чисел множини Ώ — буде дискретною.

Означення 2. Співвідношення, що встановляє зв’язок між можливими значеннями випадкової величини та відповідними їм імовірностями, називають законом розподілу випадкової величини.

У разі табличної форми запису закону подається послідовність можливих значень випадкової величини Х, розміщених у порядку зростання, та відповідних їм імовірностей:

Х = хі	х 1	х 2	х 3	......	хk
Р (Х = хі) = рі	р 1	р 2	р 3	.....	рk

Оскільки випадкові події (Х = х_j) і (Х = х_m) є між собою несумісними ((Х = х_і) ∩ (Х = х_m) = Æ, і 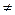m; і, m = 1, 2, …, k) і утворюють повну групу 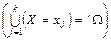, то необхідною є така умова:

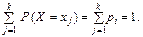(1)

Означення 3. Рівність (1) називають умовою нормування для дискретної випадкової величини Х. Наведену таблицю називають рядом розподілу.

Приклад 2. Закон розподілу дискретної випадкової величини Х задано таблицею

Х = хі	–4
Р (Х = хі) = рі	0,1	0,1	0,5	р 4	0,2

Знайти ймовірність можливого значення випадкової величини Х = х ₄ = 5.

Розв’язання. Згідно з умовою нормування (61) маємо:

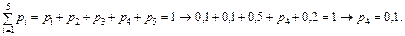
Завдання. За заданим законом розподілу дискретної випадкової величини Х маємо:

Х = хі	– 4	–1
Р (Х = х і)= рі	а	1,5 а	0,5 а	3,5 а	2,5 а	а

Знайти а. Обчислити: P (X < 2), P (– 4 < X 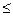8).

Дата добавления: 2014-11-18