Урок №68

Контрольні запитання.

1. Яка величина називається випадковою?

2. Яка величина називається дискретною?

3. Що називається законом розподілу випадкової величини?

4. Що називається рядом розподілу випадкової величини?

Література: [1] – Розділ 11.

Тема: Числові характеристики випадкових величин.

План

1. Поняття дискретної випадкової величини.

2. Математичне сподівання.

3. Дисперсія.

Величина називається випадковою, якщо вона набуває своїх значень в залежності від наслідків деякого випробування, при чому для кожного елементарного наслідку вона має єдине значення. Якщо ці значення можна записати у вигляді послідовності (скінченої, або нескінченої), то випадкова величина називається дискретною.

Якщо величина Х набуває значень Х₁, Х₂,......,Х_n,...... з відповідними ймовірностями Р₁, Р₂,......,Р_n,......, то кажуть, що задано закон розподілу ймовірностей випадкової величини, який зручно записувати у вигляді таблиці

Х1	Х2	Х3	...	Хn	...
Р1	Р2	Р3	...	Рn	...

де 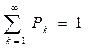(1)

або пар чисел .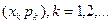

Важливим числовими характеристиками випадкової величини є математичне сподівання і дисперсія цієї величини.

Математичним сподіванням випадкової величини називається число, яке дорівнює сумі добутків усіх значень випадкової величини на ймовірності цих значень. Отже,

, або (2)

Точку з координатою МХ називають центром розсіювання ймовірностей.

У механічній інтерпретації М(Х) – це центр системи мас (ймовірностей), розподілених дискретно вздовж осі абсцис так, що на точку з абсцисою К, припадає маса (ймовірності) р_к, при чому

(загальна маса ймовірностей дорівнює (1), бо

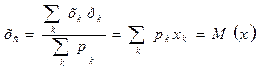
Випадкову величину Х = М(Х) називають відхиленням.

Дисперсію випадкової величини називають математичне сподівання квадрата відхилення цієї величини від її математичного сподівання і позначають D(Х). Отже,

(3)

Для обчислення дисперсій більш зручною є формула

(4)

Дисперсія випадкової величини характеризує ступінь розсіювання й ймовірностей навколо математичного сподівання. У механічній інтерпретації дисперсія – це момент інерції відносно центра мас з загальною одиничною масою, розподіленою вздовж осі абсцис так, що в точці з абсцисою Х_к знаходиться маса Р_к. Часто для характеристики розсіювання ймовірностей користуються не дисперсією, а так званим середнім квадратичним відхиленням R(x)(або стандартом), яке дорівнює

(5)

Основні властивості числових характеристик.

1. М(С) = С, С = const

2. M (X+Y) = M(X) + M(Y);

3. М(ХY) = M(X)∙M(Y);

4. M(CX) = CM(X), C = const;

5. D(C) = 0 C = const;

6. D(X+Y) = D(X) + D(Y);

7. D(CX) = C²D(X); C = const;

8. D(X-Y) = D(X) + D(Y).

Приклад. Дискретна випадкова величина розподілена за законом:

Х	-1
Р	0,2	0,1	0,3	0,4

Знайти D(X).

Розв’язання.

М(Х) = -1∙0,2 + 1∙0,3 + 2∙0,4 = 0,9, а потім

М(Х²) = 1∙0,2 + 0∙0,1 + 1∙0,3 + 4∙= 2,1

За формулою (4) маємо

D(Х) = М(Х²) – М²(Ч) = 2,1 – 0,81 = 1,29.

Дата добавления: 2014-11-18