Параметри статистичних розподілів

Закони розподілу випадкових величин

Параметри статистичних розподілів ТА

Результати окремих експериментів, як ми вже відмічали, непередбачувані, але це не означає, що вони не підлягають ніяким закономірностям. Закони, якими описуються результати вимірювання існують і мають статистичний характер. При обробці експериментальних результатів ставиться завдання – встановити ці закони і скористатися ними для досягнення основної мети – отримати із досліду якнайкращу оцінку істинного значення вимірюваної величини і охарактеризувати якість цієї оцінки. Отже, математичні закони теорії ймовірності не є безпредметними абстракціями, позбавленими фізичного змісту, вони є математичним виразом реальних закономірностей, що фактично існують в масових випадкових явищах природи. Розробка методів реєстрації, опису і аналізу статистичних експериментальних даних, що отримуються в результаті спостереження масових випадкових явищ, є предметом спеціальної науки - математичної статистики. Залежно від характеру практичного питання і від об’єму наявного експериментального матеріалу ці завдання можуть приймати ту або іншу форму. Найбільш типові завдання математичної статистики, що часто зустрічаються на практиці при проведенні медико-біологічних досліджень:

1. Завдання з визначення закону розподілу випадкової величини (або системи випадкових величин) за статистичними даними.

2. Задача перевірки справедливості гіпотез.

3. Знаходження взаємозв’язку між явищами.

Величина 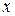, що є результатом досліду, як правило є випадковою величиною, тобто заздалегідь непередбачувана і змінюється від досліду до досліду. Провівши дослід з нескінченної кількості вимірювань, ми отримаємо генеральну сукупність - повний набір всіх значень, які може приймати випадкова величина. У реальних умовах дослід проводиться скінченну кількість раз, і ми отримуємо вибірку, що складається із скінченного числа значень випадкової величини. Це число називається об’ємом вибірки. Генеральна сукупність - граничний випадок вибірки з нескінченно великим об’ємом. Між параметрами вибірки і параметрами генеральної сукупності є принципова відмінність. Якщо узяти декілька вибірок одного і того ж об’єму n, тобто провести декілька серій дослідів або n вимірювань в кожній серії, то, через випадковий характер вимірюваних величин, параметри вибірок відрізнятимуться один від одного. Іншими словами, параметри серій вимірювань (наприклад, середні значення результатів вимірювань в серії) є випадковими навіть за незмінних умов досліду. Параметри ж генеральної сукупності за заданих умов досліду незмінні. Тому спочатку розглянемо параметри генеральної сукупності, які математично описуються простіше, ніж параметри вибірки.

Параметри генеральної сукупності:

1. Середнє значення 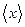(або математичне очікування ())

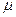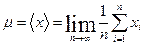. (1)

Середнє значення, що відповідає нескінченному числу вимірювань, позначатимемо 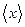, щоб відрізнити його від середнього значення 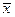, що відповідає серії з n вимірювань. При відсутності похибок воно співпадає з істинним значенням вимірюваної величини.

2. Дисперсія - середній квадрат відхилення випадкової величини від середнього значення

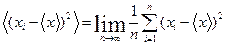= (2)

3. Середньоквадратичне (стандартне) відхилення 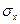, що характеризує розкид випадкових величин:

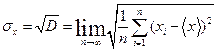(3)

Величину 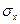називають також середньоквадратичною похибкою.

При обробці результатів вимірювань важливе значення має закон додавання дисперсій:

.

Він завжди використовується тоді, коли потрібно визначити похибки результату, обумовленого сукупністю різних незалежних факторів.

Дата добавления: 2014-11-18