Закономерности и коэффициенты явлений переноса

Экспериментально установлено, что перенос массы вещества при явлении диффузии подчиняется закону А. Фика: масса газа ΔM, которая переносится за единицу времени через взятый внутри газа элемент поверхности, площадь которого равна единице, прямо пропорциональна скорости изменения плотности газа ρ на единицу длины х в направлении нормали n к рассматриваемой площадке:

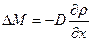
(3.1)

Если элемент поверхности выбран так, что нормаль n совпадает с направлением наиболее быстрого убывания плотности ρ, то 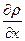численно равно градиенту плотности. Величина D называется коэффициентом диффузии. Коэффициент диффузии есть физическая величина, численно равная массе вещества, переносимого через единицу поверхности за единицу времени при градиенте плотности, равном единице. В Международной системе единиц СИ коэффициент диффузии измеряется в м²/сек. Знак минус в формуле (3.1) указывает, что перенос массы происходит в направлении убывания плотности.

Явление внутреннего трения, как показал опыт, подчиняется закону И. Ньютона:

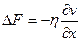
(3.2)

где ΔF - сила внутреннего трения, действующая на единицу площади поверхности слоя, 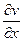- изменение скорости движения слоев на единицу длины х в направлении внутренней нормали к поверхности слоя.

Знак минус в формуле (3.2) показывает, что сила ΔF про­тивоположна по направлению производной по х от вектора v ско­рости движения газа. Величина h называется коэффициентом внутреннего трения, или динамической вязкостью, и измеряется в Международной системе единиц СИ в кг/м · сек, или н · сек/м². Коэффициент внутреннего трения численно равен силе внутреннего трения, действующей на еди­ницу площади поверхности слоя при градиенте скорости, равном единице. Помимо динамической вязкости применяется также кинематическая вязкость 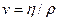(ρ - плотность), измеряемая и Международной системе единиц СИ в м²/сек.

Явление теплопроводности возникает, если различные слои газа имеют разную температуру, т. е. обладают различной внутренней энергией. Процесс передачи внутренней энергии в форме теплоты происходит так, что количество теплоты ΔQ, переносимое за единицу времени через единичную площадку, прямо пропорционально скорости изменения температуры на единицу длины х в направлении нормали n к этой площадке:

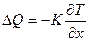
(3.3)

Формула (3.3) была установлена Ж. Фурье и называется законом теплопроводности Фурье. В формуле (3.3) К - коэффициент теплопроводности, а знак минус показывает, что энергия пере­носится в сторону убывания температуры. Коэффициент тепло­проводности показывает, какое количество теплоты переносится через единицу площади за единицу времени при градиенте тем­пературы, равном единице. В Международной системе единиц СИ коэффициент теплопроводности измеряется в дж/м · сек · град.

Строго говоря, законы Фика, Ньютона и Фурье являются дифференциальными законами, справедливыми для малой пло­щадки dS и малого промежутка времени dτ. Поэтому их нужно записывать в таком виде:

	(3.4)
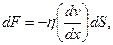
	(3.5)
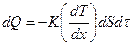
	(3.6)

Эти формулы совпадают с написанными выше, если под ΔМ, ΔF и ΔQ понимать следующие выражения: 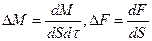и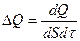

Закономерности всех явлений переноса сходны между собой. Выражения (3.1) - (3.6) являются макроскопическими и не вскрывают молекулярно-кинетического смысла коэффициентов переноса D, h и К. Задача кинетической теории состоит в установлении связи между этими коэффициентами и микрохарактери­стиками теплового движения молекул (средней длиной свободного пробега, средней скоростью молекул, их энергией и т. п.).

Перенос массы:

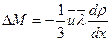
(3.7)

Уравнение (3.7) совпадает с (3.1). Следовательно, для коэф­фициента диффузии D имеем следующее выражение:

(3.8)

Выражения для коэффициентов теплопроводности и внутреннего трения:

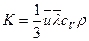
	(3.9)
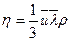
	(3.10)

где 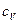- удельная теплоемкость газа в изохорическом процессе.

Из формул для коэффициентов переноса вытекают некоторые важные выводы. Оказывается, что коэффициенты внутреннего трения и теплопроводности не зависят от давления газа. Между коэффициентами переноса существуют простые зависимости, вытекающие из формул (3.7)-(3.10):

и

(3.11)

Эти формулы показывают, что по найденным из эксперимента значениям коэффициента внутреннего трения, теплопроводности или диффузии можно определить остальные коэффициенты переноса.

В таблице 1 (см. приложение) приведены полученные из экспериментов значения коэффициентов К, 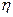и величины 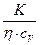для ряда газов при t = 0° С. Из этой таблицы хорошо виден приближенный характер рассмотренной теории явлений переноса. Учет взаимодействия между соударяющимися молекулами и их распределения по скоростям в условиях наличия градиентов плотности, температуры или скорости не изменяет физического смысла результатов, но приводит к другим значениям числовых множителей. Этим до­стигается лучшее согласие теории с данными экспериментов.

На основании экспериментального исследования явлений переноса в химически однородных газах можно оценить величины «эффективных» диаметров d молекул.

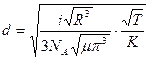
(3.12)

и

(3.13)

Найти «эффективный» диаметр d его молекул можно по табл. 2 (см. приложение).

В заключении приведем сводную таблицу явлений переноса.

Таблица 1. Сводная таблица явлений переноса

Явление	Переносимая физическая величина	Уравнение переноса	Формула для коэффициента переноса
Диффузия	Масса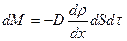
Внутреннее трение	Импульс
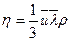
Теплопроводность	Внутренняя энергия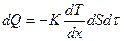

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ТЕМЕ: «ЯВЛЕНИЯ ПЕРЕНОСА»

Задача 3.1. Найти коэффициент диффузии D и вязкость η воздуха при давлении р = 101,3 кПа и температуре t = 10 ⁰ С. Диаметр молекул воздуха σ = 0,3 нм.

Дано: р = 101,3 кПа t = 10^0 С σ = 0,3 нм	Решение: 1. Согласно уравнениям (1.14), (3.12) и (3.13), можно получить:   2. Из (3.8), (3.10), имеем:
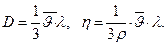
Найти: D -? η -?

3. Согласно уравнению состояния идеального газа, имеем: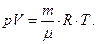

4. Решая совместно систему уравнений: ,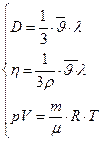

можно получить: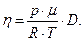

5. Вычисления производим в Международной системе СИ:

Ответ: D = 1,45ּ10^-5 м²/с; η = 18,2 мкПа·с.

Задача 3.2. Найти среднюю длину свободного пробега атомов гелия в условиях, когда плотность гелия r = 2,1 × 10^-2 кг/м³, а эффективный диаметр атома гелия d = 1,9 ּ 10^{-10 м.}

Дано: r = 2,1 × 10^-2 кг/м³ d = 1,9 ּ 10^{-10 м}

Решение: 1. Средняя длина свободного пробега определяется следующим выражением:

(1)

Найти: <λ> -?  

2. Из основного уравнения МКТ имеем, p = nkT. Используя основное уравнение МКТ, имеем: pV = νRT.

3. Подставляя уравнения в (1), получим: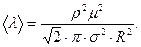

4. Вычисления производим в Международной системе единиц СИ:

<λ> = 641,3 ּ10⁶ м.

Ответ: <λ> = 641,3 ּ10⁶ м.

Дата добавления: 2014-11-18