Турбулентное течение в трубах

Расчет турбулентного течения в трубах относится к широко распространенным инженерным задачам. Одним из важных элементов расчета является нахождение закона распределения осредненных скоростей в поперечном сечении трубы.

По Прандтлю, поток в трубах при турбулентном течении ус­ловно разбивается на две области (двухслойная модель Прандтля): турбулентное ядро, в котором определяющими являются напряжения Рейнольдса, и тонкий вязкий подслой (ламинарный подслой по Прандтлю либо пристенный слой) вблизи стенки, в котором влияние турбулентности пренебрежимо мало, а касательные напряжения обусловлены физической вязкостью в соответствии с законом трения Ньютона.

На рис. 4.2 приведен примерный вид поля осредненных скоростей (эпюра скорости) при турбулентном течении в трубопроводе.

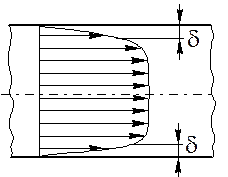
Рис. 4.2.

Эпюра скорости при турбулентном течении

В пределах подслоя скорость изменяется по линейному закону. Величина t₀/r имеет размерность квадрата скорости, поэтому корень квадратный из нее, т.е.

(4.16)

называют динамической скоростью либо скоростью трения.

Таким образом, динамическая скорость является мерой интенсивности турбулентного пульсационного движения, т.е. мерой интенсивности переноса количества движения.

Согласно наиболее простой гипотезе, принадлежащей Л.Прандтлю,

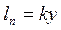(4.17)

где k - величина, называемая постоянной Кармана. Выполненные измерения показывают, что k» 0,4.

Вторым является допущение о касательных напряжениях, т.е. t_Т = t₀.

При этих допущениях формула Прандтля принимает вид

либо

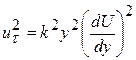
Использование двухслойной модели, т.е. разделение потока на ядро и пристенный слой, приводит к специфической классификации стенок труб. Если толщина пристенного слоя больше выступов шероховатости, трубы называют гидравлически гладкими, в противном случае - шероховатыми.

На рис. 4.3 приведены графики, характеризующие распределение длины пути перемешивания в поперечном сечении круглой трубы по данным опытов Никурадзе (кружки) и по формулам, предложенным различными авторами. В соответствии с результатами экспериментов, значение l_n достигает максимума на оси трубы. Из графика следует, что гипотеза Прандтля (прямая 1) неприемлема.

Рис. 4.3.

Кривые распределения длины пути перемешивания по сечению трубы

Существенно отличаются от опытной и кривые, полученные другими авторами: Карманом (кривая 2), Конаковым (кри­вая 4), Саткевичем (кривая 7). Достаточно близка к эксперименту кривая Альтшуля (кривая 3), описывающая длину пути перемешивания с помощью формулы

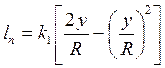(4.18)

В последнее время Д.Н.Васильевым получена аппроксимирующая зависимость, практически точно совпадающая с данными опыта и имеющая вид

(4.19)

Дата добавления: 2014-11-18