Задачи для самостоятельного решения. 2. 1. Найти скорость V течения углекислого газа по трубе, если известно, что за время t=30 мин через поперечное сечение трубы протекает масса газа m = 0,51 кг

2.1. Найти скорость v течения углекислого газа по трубе, если известно, что за время t =30 мин через поперечное сечение трубы протекает масса газа m = 0,51 кг. Плотность газа p = 7,5 кг/м³. Диаметр трубы D = 2 см.

2.2. В дне цилиндрического сосуда диаметром D = 0,5 м имеется круглое отверстие диаметром d = 1 см. Найти зависимость скорости понижения уровня воды в сосуде от высоты h этого уровня. Найти значение этой скорости для высоты h = 0,2 м.

2.3. На столе стоит сосуд с водой, в боковой поверхности которого имеется малое отверстие, расположенное на расстоянии h₂ от уровня воды. Уровень воды в сосуде поддерживается постоянным. На каком расстоянии l от сосуда (по горизонтали) струя падает на стол в случае, если а) h₁ = 25 см, h₂ = 16 см; б) h₁ = 16 см, h₂ = 25 см?

2.4. Сосуд, наполненный водой, сообщается с атмосферой через стеклянную трубку, закрепленную в горлышке сосуда. Кран K находится на расстоянии h₂ = 2 см от дна сосуда. Найти скорость v вытекания воды из крана в случае, если расстояние между нижним концом трубки и дном сосуда: а) h₁ = 2 см; б) h₁ = 7,5 см; в) h₁ = 10 см;

2.5. Цилиндрический бак высотой h = 1 м наполнен до краев водой. За какое время t вся вода выльется через отверстие, расположенное у дна бака, если S₂ поперечного сечения отверстия в 400 раз меньше площади поперечного сечения бака? Сравнить это время с тем, которое понадобилось бы для вытекания того же объема воды, если бы уровень воды в баке поддерживался постоянным на высоте h = 1 м от отверстия.

2.6. В сосуд льется вода, причем за единицу времени наливается объем воды V_t = 0,2 л/с. Каким должен быть диаметр d отверстия в дне сосуда, чтобы вода в нем держалась на постоянном уровне h = 8,3 см?

2.7. Какое давление p создает компенсатор в краскопульте, если струя жидкой краски вылетает из него со скоростью v = 25 м/с? Плотность краски ρ =0,8 ×10³ кг/м³.

2.8. По горизонтальный трубе АВ течет жидкость. Разность уровней этой жидкости в трубах a и b равна ∆h = 10 см. Диаметры трубок a и b одинаковы. Найти скорость v течения жидкости в трубе АВ.

2.9. Воздух продувается через трубку АВ. За единицу времени через трубку АВ протекает объем воздуха V_t =5 л/мин. Площадь поперечного сечения широкой части трубки АВ равна S₁ =2см², а узкой её части и трубки abc равна S₂ = 0,5см². найти разность уровней ∆h воды, налитой в трубку abc. Плотность воздуха ρ =1,32 кг/м³.

2.10. Шарик всплывает с постоянной скоростью v в жидкости, плотность ρ₁ которой в 4 раза больше плотности материала шарика. Во сколько раз сила трения F_тр, действующая на всплывающий шарик, больше силы тяжести mg, действующей на этот шарик?

2.11. Какой наибольшей скорости v может достичь дождевая капля диаметром d =0,3 мм, если динамическая воздуха m = 1,2×10 ^-5 Па×с?

2.12. Стальной шарик диаметром d = 1 мм падает с постоянной скоростью v = 0,185 см/с в большом сосуде, наполненном сосуде поддерживаесяв боковой поверхности которого имеется малое отверстие, рассположенное касторовым маслом. Найти динамическую вязкость η касторового масла.

2.13. Смесь свинцовых дробинок с диаметрами d₁ = 3 мм и d₂ = 1 мм опустив в бак с глицериновой высотой h = 1м. На сколько позже упадет на дно дробинки меньшего диаметра по сравнению с дробинками большего диаметра? Динамическая вязкость глицерина η = 1,47 Па×с.

2.14. Пробковый шарик радиусом r = 5 мм всплывает в сосуде, наполненным касторовым маслом. Найти динамическую и кинетическую вязкость касторового масла, если шарик всплывает с постоянной скоростью v = 3,5 см/с.

2.15. В боковую поверхность цилиндрического сосуда радиусом R = 2 см вставлен горизонтальный капилляр, внутренний радиус r =1мм которого и длина l = 2 см. В сосуд налито касторовое масло, динамическая вязкость которого η =1,2 Па×с. Найти зависимость скорости v понижения уровня касторового масла в сосуде от высоты h этого уровня над капилляром. Найти значение этой скорости при h = 26 см.

2.16. В боковую поверхность сосуда вставлен горизонтальный капилляр, внутренний радиус которого r = 1 мм и длина l = 1,5 см. В сосуд налит глицерин, динамическая вязкость которого η = 1,0 Па×с. Уровень глицерина в сосуде поддерживается постоянным на высоте h = 0,18 м выше капилляра. Какое время потребуется на то, чтобы из капилляра вытек объем глицерина V = 5 см³?

2.17. На столе стоит сосуд, в боковую поверхность которого вставлен горизонтальный капилляр на высоте h₁ = 5см от дна сосуда. Внутренний радиус капилляра r = 1 мм и длина l = 1см. В сосуд налито машинное масло, плотность которого ρ = 0,9×10³ кг/м³ и динамическая вязкость η = 0,5 Па×с. Уровень масла в сосуде поддерживается постоянным на высоте h₂ = 50 см выше капилляра. На каком расстоянии L от конца капилляра (по горизонтали) струя масла падает на стол?

2.18. Стальной шарик падает в широком сосуде наполненном трансформаторным маслом, плотность которого ρ = 0,9×10³ кг/м³ и динамическая вязкость η = 0,8 Па×с. Считая, что закон Стокса имеет место при числе Рейнольдса Re 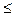0,5 (если при вычислении Re в качестве величины D взять диаметр шарика), найти предельное значение диаметра D шарика.

2.19. Считая, что ламинарность движения жидкости (или газа) в цилиндрической трубе сохраняется при числе Рейнольдса Re 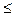3000 (если при вычислении Re в качестве величины D взять диаметр труды), показать, что условия задачи 4.1 соответствуют ламинарному движению. Кинетическая вязкость газа v = 1,33×10^-6 м²/с.

2.20. Вода течет по трубе, причем за единицу времени через поперечное сечение трубы протекает объем воды V _t = 200 см³/с. Динамическая вязкость воды η = 0,001 Па×с. При каком предельном значении диаметра D трубы движение воды остается ламинарными? (Смотри условие предыдущей задачи.)

Дата добавления: 2014-11-18