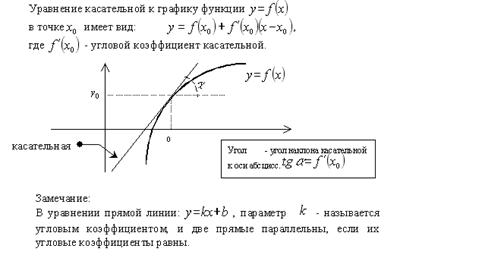
Первообразная. Уравнения касательной функции

Наклонная

Горизонтальная

Горизонтальная асимптота — прямая вида y = a при условии существования предела

lim x →±∞ f (x)= a.

Наклонная асимптота — прямая вида y = kx + b при условии существования пределов

Пример наклонной асимптоты

1. lim x →±∞ f (x) x = k

2. lim x →±∞(f (x)− kx)= b

Замечание: функция может иметь не более двух наклонных (горизонтальных) асимптот.

Замечание: если хотя бы один из двух упомянутых выше пределов не существует (или равен ∞), то наклонной асимптоты при x →+∞ (или x →−∞) не существует.

Первообрáзной или примитивной функцией (иногда называют также антипроизводной) данной функции 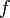называют такую , производная которой (на всей области определения) равна 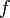, то есть . Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.

Так, например, функция является первообразной . Так как производная константы равна нулю, будет иметь бесконечное количество первообразных, таких как или 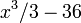и т. д.; таким образом семейство первообразных функции можно обозначить как 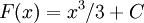, где 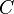— любое число. Графики таких первообразных смещены вертикально относительно друг друга, и их положение зависит от значения .

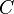Первообразные важны тем, что позволяют вычислять интегралы. Если — первообразная интегрируемой функции 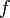, то:

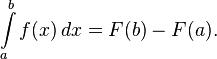
Это соотношение называется формулой Ньютона — Лейбница.

Касательная прямая — прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.

Производная в точке x ₀ равна угловому коэффициенту касательной к графику функции y = f (x) в этой точке.

Неопределённый интеграл. Методы интегрирования.

Функция F(x), дифференцируемая в данном промежутке X, называется первообразной для функции f(x), или интегралом от f(x), если для всякого x ∈X справедливо равенство:

F^' (x) = f(x).

Нахождение всех первообразных для данной функции называется ее интегрированием. Неопределенным интегралом функции f(x) на данном промежутке Х называется множество всех первообразных функций для функции f(x); обозначение - ∫ f(x) dx.

Неопределённый интеграл для функции 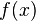— это совокупность всех первообразных данной функции.

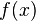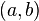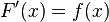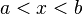Если функция определена и непрерывна на промежутке и — её первообразная, то есть при , то

,

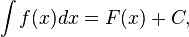
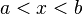где С — произвольная постоянная.

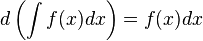
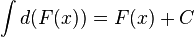
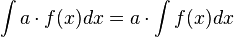
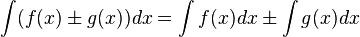
Если 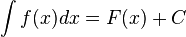, то и 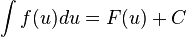, где 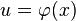— произвольная функция, имеющая непрерывную производную

Дата добавления: 2014-11-08