Тест 8. Случайные величины

Методические указания.

Тест 7. ПОНЯТИЕ ВЕРОЯТНОСТЙ

Задача. Партия изделий содержит B процентов брака. Какого объема n должна быть контрольная выборка, чтобы с вероятностью P обнаружить в ней хотя бы одно бракованное изделие?

B=(W)_mod16+8, P=0.95+DP, DP=(-1)^W´ .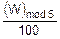

1. Данный случайный эксперимент отвечает схеме Бернулли.

2. Событие «хотя бы одно бракованное изделие» противоположно событию «ни одного бракованного изделия».

Задача. Плотность вероятности f(t) времени реакции t наряда вневедомственной охраны на сигнал тревоги задана графиком на рис. 2.

0. Вычислить значение параметра T по формуле

T= 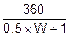с.

1. Записать аналитическое выражение для f(t).

2. Найти значение параметра H из условия

.

3. Найти аналитическое выражение для функции распределения F(t) случайной величины t.

4. Определить числовые характеристики случайной величины t:

· ее математическое ожидание m_t,

· дисперсию D_t,

· среднеквадратическое отклонение s_t.

5. Вычислить P(a<t<b) – вероятность попадания СВ t в интервал ]a,b[, где

a=m_t-0.05´W´s_t, b=m_t+2´s_t.

Пример. W=22.

Плотность вероятности f(t) задана графиком на рис. 3.

Решение.

0. Вычислим значение параметра T:

T= 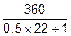=30.0 с.

1. В нашем случае f(t) состоит (рис. 3) из трех фрагментов: f_n(t)=0 при t<0, отрезка прямой f_p(t)=k´t+b при 0£t£T и f_r(t)=0 при t>T, то есть

f(t)=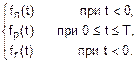

Найдем параметры b и k прямой f_p(t), подставив в ее уравнение координаты точек (0,H) и 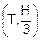, через которые она проходит:

b=H, k= .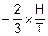

Так получим следующее аналитическое выражение для f(t):

f(t)= 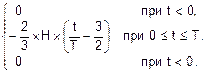. (1)

2. Значение H находим из условия

.

С учетом того, что только фрагмент f_p(t) функции f(t) отличен от 0 (рис. 3), можем записать:

.

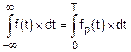Последний интеграл представляет собою площадь трапеции с основаниями H, 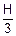и высотой T (рис. 3). Эта площадь и равна 1:

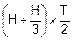=1. H= 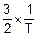=0.05 с^-1.

Подставив значение H в (1), получим окончательно

f(t)=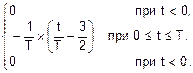

3. По определению (8.5)

F(t)= .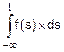

Ранее мы отметили, что функция f(t) состоит из трех фрагментов. Очевидно, что и функция F(t) тоже разбивается на три фрагмента: F_n(t) при t<0, F_p(t) при 0£t£T и F_r(t) при t>T:

F(t)= 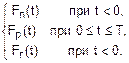. (2)

При этом

F_n(t)= 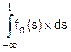=0, F_p(t)=F_n(0)+ = = ,

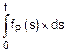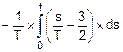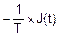F_r(t)=F_p(T)+ = =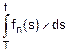

= = .

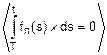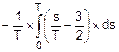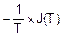Найдем выражение для J(t) и значение для J(T).

J(t)= .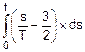

Этап 1.

FJ(s)= = =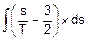

= = .

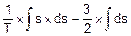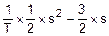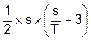Этап 2.

J(t)= = .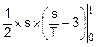

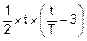J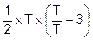(T)= =-T.

Далее

F_p(t)= 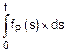= 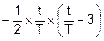, F_r(t)=F_p(T)=1.

Подставив полученные результаты в (2), запишем такое аналитическое выражение для F(t):

F(t)= .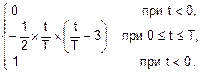

4. Числовые характеристики непрерывной СВ t, а именно, ее математическое ожидание, дисперсию и СКО вычисляем по их определениям (8.13), (8.14) и (8.10), соответственно.

Математическое ожидание:

m_t= = = .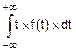

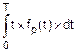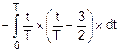Этап 1.

Fm(t)= =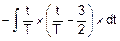

= =

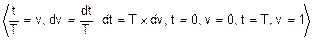=-T´ 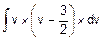=-T´ =

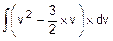= =Fm(v).

Этап 2.

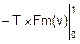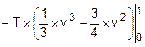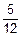m_t= = =

= ´T= 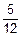´30=12.50 c.

Дисперсия:

D_t= = =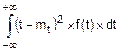

= =

= .

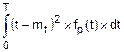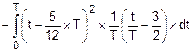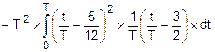Этап 1.

FD(t)= =

= =

= =

= =

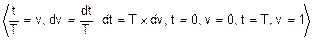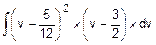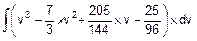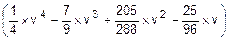= =FD(v).

Этап 2.

D_t=-T²´ 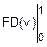= = 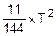=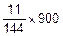68.75 c².

СКО:

s_t= 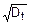= = 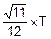=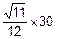8.29 c.

5. По определению (8.6)

P(a<t<b)=F(b)-F(a).

a=m_t-0.05´W´s_t= 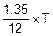=3.38,

b=m_t+2´s_t= 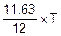=29.08.

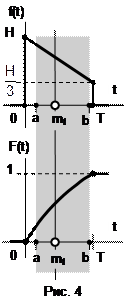
Полученные результаты отобразим на графиках (рис. 4).

Далее

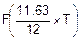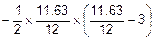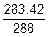= = =0.98.

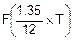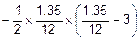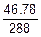= = =0.16.

Значит,

P(a<t<b)=0.98-0.16=0.82.

Дата добавления: 2014-11-18