Изображение плоскости на комплексном чертеже

Теорема о проецировании прямого угла

Если одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то прямой угол на эту плоскость проекций проецируется без искажения.

Доказательство (рисунок 1.3.11). По условию АВ^ВС и АВ//П¹. На основании прямоугольного проецирования АВ^ВВ¹, следовательно, АВ_┴γ(ВС∩ВВ¹), так как АВ^ВС и АВ^ВВ¹.

По условию АВ//А¹В¹, следовательно А¹В¹_┴γ, т.е. и к прямой В¹С¹ этой плоскости. Значит угол между прямыми А¹В¹ и В¹С¹ равен 90º.

Из теоремы следует, что если одна сторона прямого угла является прямой уровня, то прямой угол проецируется без искажения на плоскость проекций, параллельную этой стороне.

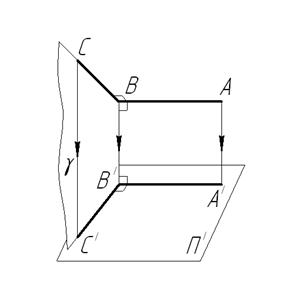
Рисунок 1.3.11 – Проецирование прямого угла

Плоскость можно задать:

- тремя точками, не лежащими на одной прямой;

- прямой и точкой, не лежащей на этой прямой;

- двумя пересекающимися прямыми;

- двумя параллельными прямыми;

- отсеком.

Наиболее наглядным является задание плоскости отсеком. Простейшим из отсеков является треугольник.

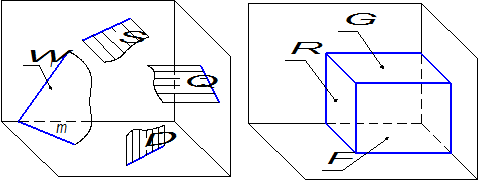
Рисунок 1.3.12 – Положение плоскости относительно плоскостей проекций

Как и в случае с прямыми линиями различают плоскости общего и частного положения. Плоскости, наклонённые ко всем плоскостям проекций, называются плоскостями общего положения (например, плоскость W на рисунке 1.3.12). Плоскости, перпендикулярные либо параллельные плоскости проекций, называются плоскостями частного положения (в соответствии с рисунком 1.3.12 это плоскости S, D, Q, Г, Ф, Р ).

По аналогии с прямыми линиями плоскости частного положения разделяются на проецирующие плоскости, т.е. перпендикулярные плоскости проекций (плоскости S, D, Q на рисунке 1.3.12) и плоскости уровня – параллельные плоскости проекций (плоскости Г, Ф, Р).

Плоскость общего положения, как и прямая общего положения, может быть восходящей и нисходящей. На комплексном чертеже проекции восходящей плоскости ориентированы одинаково, а нисходящей – противоположно. Изображение нисходящей плоскости соответствует рисунку 1.3.16.

Дата добавления: 2014-11-18